
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
ou Carthage et la légende de Didon |

Nous somme ici en bord de mer, face au Bou Kornine, près de Tunis. Nous allons définir notre domaine et procéder à la (re) construction de Carthage...
Légende et histoire du problème : »
Les points A(a) et B(b) sont donnés sur (Ox). il nous faut trouver la nature de la courbe (c) décrite par notre lanière de cuir, de longueur donnée l, afin que l'aire intérieure obtenue, entre (c) et l'axe des abscisses, soit maximale.
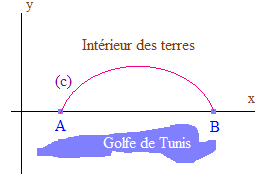
Recherchons cette courbe sous la forme y = f(x), quitte à paramétrer ultérieurement. La longueur de la lanière est donnée par la formule :
![]()
Nous devons alors chercher à maximiser l'aire sous la courbe (c), à savoir :
![]()
C'est un problème isopérimétrique : maximiser une aire pour un périmètre donné. Nous utilisons l'équation d'Euler-Lagrange : la fonctionnelle est tout simplement ici y = f(x) : elle ne dépend directement que de x. Sous la contrainte ci-dessus, on applique alors l'équation l'équation d'Euler-Lagrange à :
![]()
où λ est le multiplicateur de Lagrange. G ne dépend pas directement de x, on a alors une équation de la forme G - y'G'y' = k (constante), soit :

Isolons les radicaux, élevons au carré et multiplions le tout par (1 + y'2), il ne reste alors que :
![]()
Posons Y = y - k, isolons y'2, remplaçons par (dy/dx)2, remarquons que dY = dy. Nous aurons alors :
![]()
D'où l'intégration immédiate que l'on peut écrire avec une constante additive C arbitraire, suivie d'une élévation au carré :
(x - C)2 + (y - k)2 = λ2 : équation d'un cercle de centre ω (C,k) de rayon λ
Il s'agira donc dans notre problème d'un arc de cercle. Son abscisse C est (a + b)/2. La solution trouvée est extrémale, c'est à dire minimale ou maximale. Elle ne peut être minimale car l'arc de cercle (c) étant tracé, il est bien évident que l'on peut considérer une infinité d'autres possibilités sous cet arc.
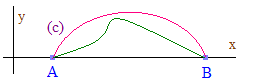
On peut évidemment exprimer y en fonction de x mais ce n'est pas indispensable. La connaissance de d et l permet de déterminer le rayon λ, donc la valeur de k, ordonnée de ω. Mais la construction n'est pas simple. Elle n'est pas possible au sens euclidien. Suivant les valeurs de l et de d, l'arc dépassera ou non un demi-cercle : si l > πd/2, le centre ω est au-dessus de (AB) et l'arc dépasse un demi-cercle; sinon ω est au-dessous de (AB) et l'arc est moindre qu'un demi-cercle.
| Prenons un exemple : a = 1, b = 5, l = 10 |
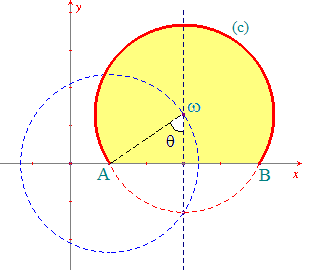
On a ici d = 4, donc l > πd/2 et ω est au-dessus de (AB). Rebaptisons R le rayon de (c). On a L/2 = R(π - θ) et d/2 = Rsin θ. Dans notre cas, cela fournit :
![]() , 0 < θ <
π/2
, 0 < θ <
π/2
On peut :
soit résoudre une équation par une méthode approchée, comme celle de Newton ou par dichotomie : 5sin θ - 2(π - θ) = 0, dont on tirera R. Dans ces programmes JavaScript, entrez alors l'équation 5*sin(x)-2*(pi-x) et rechercher x au voisinage de 1.
soit demander à l'ordinateur de nous tracer les deux courbes d'équation y = 5sin θ et y = 2(π - θ); la connaissance de θ au point d'intersection fournira R.
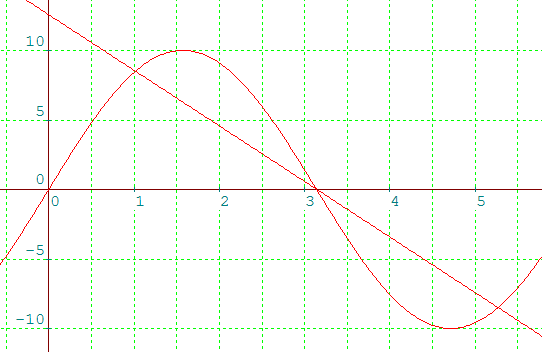
soit tracer les fonctions les fonctions exprimant R comme définies ci-dessus : on aura alors simultanément θ en abscisse et R en ordonnée au point d'intersection.
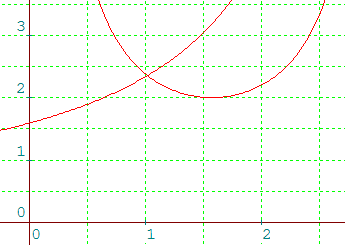
point d'intersection de y
= 2sinx et de y
= 5/(π - x)
Par usage de la troisième option, ci-contre, on obtient graphiquement, en zoomant convenablement, une très bonne précision : θ = 1,02 et R = 2,35. La méthode de Newton appliquée à la fonction 5/(pi - x) - 2/sin(x), fournit x (donc ici θ) comme valant 1,016347..., d'où R = 2,352669...
Nous convenons de retenir R = 2,35 et construisons l'enceinte de Carthago-la-nouvelle : le cercle de centre A de rayon R coupe la médiatrice de [AB] en le centre ω cherché. Le domaine de la ville nouvelle est en jaune.
Seconde option : 5sin θ
- 2(π - θ)
= 0