ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Une preuve élémentaire de
l'identité d'Euler (produit eulérien)» Riemann et la fonction zêta |
Pour tout x > 1, la série de puissances Σxn est convergente et :
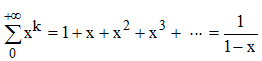
Remplaçons successivement x par 1/2s, 1/3s, 1/5s, ..., 1/ps, ... où p est un entier naturel premier et faisons le produit membre à membre. Afin de comprendre la méthode, arrêtons-nous au p-ème nombre premier, p > 5 (par exemple) :
Le développement du produit ∏p des nombres du membre de gauche de gauche est constitué de 1 et augmenté de la somme des inverses à la puissance s des nombres de la forme np = 2α3β5γ...pδ, c'est à dire 1 augmenté de la somme de tous les nombres 1/ns dont la décomposition en facteurs premiers de n possède les facteurs premiers 2, 3, 5, ... p :
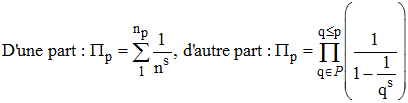
Or, quel que soit l'entier n de N, il existe p dans l'ensemble infini P des nombres premiers (» infinitude des nombres premiers), tel que n = np = 2α3β5γ...pδ (α, β, γ, ..., δ ≥ 0) et 1/ns∈∏p. Par conséquent, lorsque p augmente indéfiniment dans P, ∏p converge vers :
et finalement :
