
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Dans son traité Introductio in Analysin infinitorum de 1748, Euler procède à une vaste synthèse des connaissances en matière de fonctions (outre trigonométriques) logarithmiques et exponentielles de base a en posant, pour tout réel a strictement positif distinct de 1, l'égalité y = ax pour signifier que x est le logarithme de y dans la base a :
∀ a > 0, a ≠ 1, ∀ x : y = ax ⇔ x = loga y
Il élargit par ailleurs la définition au cas d'une variable complexe par usage de développements en série.
| Développement en série de la fonction exponentielle : |
Euler utilisait déjà (1728) la notation e (première lettre du mot exponentielle) pour la base des logarithmes népériens (qu'il dénomme à l'époque hyperbolique ) dont il donnait le développement infini (1739) comme cas particulier de celui de la fonction x → ax, développé à partir de la série du binôme de Newton pour a ≠ 1 :
En posant az = 1 + kz, puis auz = (1 + kz)u dans ladite série, Euler obtient formellement, pour tout nombre x, après quelques subtilités :
où c ne dépend que de la base a.
Si c = 1, on retrouve la série de Mercator, développement de ln(x + 1) où ln désigne la fonction logarithme népérien. Ainsi, le développement de la fonction exponentielle x → ex ne peut être que :
Développement de x → ex par la formule de Maclaurin : »
En dérivant terme à terme, sans cas de conscience pour la convergence..., on constate avec délectation que (ex)' = ex : l'exponentielle de base e est, en effet, l'unique fonction partout dérivable f telle que f ' = f.
Dans le développement précédent, si x = 1 :

soit : e = 2,7182818284590452353...
➔
Introduite autrefois en classe terminale en
tant que fonction réciproque du logarithme népérien et
aujourd'hui en tant que fonction dérivable f telle que
f![]() ' = f ou encore
telle que f(a + b) = f(a) × f(b) et de nombre dérivé 1 en zéro, la fonction
exponentielle, sa notation ex
et sa dérivation invariante (ex)' = ex
apparaissent de façon relativement naturelle. L'application de la
formule de Taylor ou de
Maclaurin conduit aisément à son
développement en série uniformément convergent.
' = f ou encore
telle que f(a + b) = f(a) × f(b) et de nombre dérivé 1 en zéro, la fonction
exponentielle, sa notation ex
et sa dérivation invariante (ex)' = ex
apparaissent de façon relativement naturelle. L'application de la
formule de Taylor ou de
Maclaurin conduit aisément à son
développement en série uniformément convergent.
∗∗∗
Étude des approches évoquées ci-dessus
Majoration de l'erreur commise dans le développement précédent :
Si, dans le développement précédent, on néglige les termes à partir du rang n + 1, on peut facilement majorer l'erreur commise en :
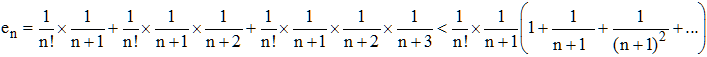
On reconnaît dans la parenthèse la sérié géométrique de 1er terme 1, de raison 1/(n+1) qui converge vers (n + 1)/n. Par suite l'erreur commise en vérifie :
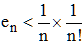
Application : afin de calculer e à 10-6 près, il nous faut en < 10-6 , soit n × n! > 106 : Par "tâtonnements", on aura tôt fait de constater qu'il faut calculer jusqu'au rang 9. d'où e ≅ 2,7182815... La 7è décimale est fausse mais c'est normal...
| Un calcul approché de e : |
Si f est une fonction dérivable, de dérivée
connue
f![]() ', on peut,
connaissant une image f(xo), calculer une
approximation de f(xo + h) si x est
suffisamment petit en utilisant la formule approchée de la dérivée :
', on peut,
connaissant une image f(xo), calculer une
approximation de f(xo + h) si x est
suffisamment petit en utilisant la formule approchée de la dérivée :
![]()
On aura : f(xo
+ h) ≃
f(xo) + hf![]() '(xo).
Posons yo
= f(xo) et y1
= f(xo
+ h). On peut itérer le procédé afin de calculer une approximation de f(xo
+ 2h) = y2. En posant xn
= xo
+ nh, on construit ainsi une suite de valeurs approchées d'images f(xn)
:
'(xo).
Posons yo
= f(xo) et y1
= f(xo
+ h). On peut itérer le procédé afin de calculer une approximation de f(xo
+ 2h) = y2. En posant xn
= xo
+ nh, on construit ainsi une suite de valeurs approchées d'images f(xn)
:
f(xn) ≃ f(xn-1)
+ hf![]() '(xn-1)
'(xn-1)
 Cette
suite de valeurs peut être entachée d'erreurs en accumulant tant les
approximations que les arrondis ! si h est trop grand, les valeurs seront
grossièrement erronées. Si h est trop petit, cela occasionnera des erreurs
d'arrondi cumulatives. Elle fut utilisée en physique par
Euler et
d'Alembert pour se donner une idée d'une courbe y =
f(x) à partir de la connaissance de sa dérivée. En l'absence d'encadrement des
valeurs trouvées, elle n'a pas, stricto sensu, de valeur mathématique !
Cette
suite de valeurs peut être entachée d'erreurs en accumulant tant les
approximations que les arrondis ! si h est trop grand, les valeurs seront
grossièrement erronées. Si h est trop petit, cela occasionnera des erreurs
d'arrondi cumulatives. Elle fut utilisée en physique par
Euler et
d'Alembert pour se donner une idée d'une courbe y =
f(x) à partir de la connaissance de sa dérivée. En l'absence d'encadrement des
valeurs trouvées, elle n'a pas, stricto sensu, de valeur mathématique !
Dans le cas de la fonction exponentielle, on a f(x) =
f![]() '(x), donc f(xn)
= (1 + h)f(xn-1) : il s'agit d'une suite
géométrique de raison 1 + h, la suite des abscisses étant arithmétique de raison
h :
'(x), donc f(xn)
= (1 + h)f(xn-1) : il s'agit d'une suite
géométrique de raison 1 + h, la suite des abscisses étant arithmétique de raison
h :
f(xn) = (1 + h)nf(xo)
Pour h = 1/10, nous obtenons f(1) = e ≃ (1,1)10 × f(0) = (1,1)10 × 1 = (1,1)10 ≃ 2,59.
Pour h = 1/100, nous obtenons e ≃ (1,01)100 ≃ 2,70
Pour h = 1/1000, nous obtenons f(1) = e ≃ (1,001)1000 × f(0) ≃ 2,717
Pour s'assurer de la convergence, on pourra étudier la belle formule ci-dessous beaucoup plus convaincant et équivalent à cette approche lorsque n est une puissance de 10 :
| Une formule rationnelle pour un nombre irrationnel et transcendant... : |
Euler prouva la belle formule qui l'amena à définir la fonction exponentielle complexe en tant que série entière :
Preuve de la formule en tant qu'exercice :
|
∗∗∗ |
Poser un = (1 + 1/n)n et vn
= ln un. |
Application de la formule au calcul approché de e : » Charles Hermite et la transcendance de e : »
➔ Le développement en série du nombre e, ainsi que son calcul approché, peuvent se faire aisément à partir de la formule de Maclaurin :
![]()
Autres calculs de e dans ChronoMath : »
| Irrationalité du nombre e : |
Euler prouva également l'irrationalité de e en utilisant le développement en fraction continue infini ci-après, dont la paternité revient à Cotes. La suite des quotients de e - 2 est :
Pour prouver l'irrationalité de e, on peut considérer les suites (un) et (vn) de termes généraux respectifs :
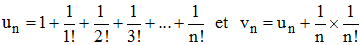
On sait que les suites (un) et (vn) convergent vers e, respectivement en croissant et décroissant (suites adjacentes). Pour tout p de N, on peut alors écrire up < e < vp . Si le nombre e est un nombre rationnel, il admet une écriture irréductible k/p et l'on a, en remplaçant et multipliant le tout par p × p! :
p × p! × up < k × p! < p × p! × up + 1.
Cet encadrement ne peut avoir lieu car les nombres p × p! × up et k × p! sont des entiers : e n'est donc pas rationnel.
Remarque : l'encadrement choisi de e par un et vn = un + 1/(n×n!) est "très serré"; on peut considérer un encadrement plus large en choisissant simplement vn = un + 1/n! fonctionnant également fort bien.
La formule d'Euler et la sublime relation liant 0, 1, e, π et i : |
Montrons tout d'abord cet important résultat fort utile dans le calcul de limites :
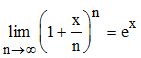
 Preuve : prendre le logarithme népérien de (1 + x/n)n, passer à la limite en utilisant ln(1 + u) ~ u
au voisinage de 0 (»
calcul élémentaire de e).
Preuve : prendre le logarithme népérien de (1 + x/n)n, passer à la limite en utilisant ln(1 + u) ~ u
au voisinage de 0 (»
calcul élémentaire de e).
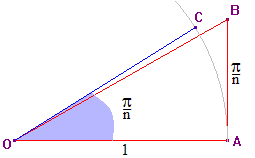
Ce résultat permet d'écrire formellement eix comme limite pour n infini de (1 + ix/n)n. Or, pour n "grand", le nombre complexe 1 + ix/n (d'image B représentée dans le plan complexe ci-dessous) correspond sensiblement au point du cercle trigonométrique d'argument x/n (d'image C), c'est à dire au nombre complexe cos (x/n) + i.sin(x/n).
En élevant à la puissance n et en utilisant la formule de De Moivre, on obtient pour n infini : lim (1 + ix/n)n = cosx + i.sinx, ce qui permet d'écrire la formule d'Euler :
eix = cosx + i.sinx (fe)
et si x = π, on obtient la sublime formule :
eiπ + 1 = 0
∗∗∗
1.
Souvent utile :
prouver que pour tout x réel, on a : 1 + eiα = 2cos(α/2)eiα/2 et
eiα - 1 = 2i sin(α/2)eiα/2
Ind. : 1 + eiα
= 1 + cosα + isinα = 2cos2(α/2) + 2isin(α/2)cos(α/2)...
»
un exemple d'application (ex. 6)
2. (indépendant de 1.) x étant distinct de tout multiple de π, prouver l'identité :
![]()
Indication : on introduira la partie imaginaire i.sin(2kx).