ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BERNOULLI Johann
(Jean),
suisse, 1667-1748 |
Frère
cadet de Jacques
Bernoulli (Jakob), Johann, dit Jean
1er, fit ses études à Bâle (Basel,
Suisse), sa ville
natale. C'est Jakob qui lui insuffla la passion des mathématiques et
l'accompagnera dans sa formation. Médecin (1690),
physicien, il fut, entre autres, le professeur de
Leonhard
Euler et un ami de Gabriel Cramer.
Pour en savoir plus sur la dynastie des Bernoulli, on pourra consulter une page (» réf.1) très intéressante de P. Radelet de Grave décrivant la généalogie de cette illustre famille de scientifiques.
Admirateur de Leibniz qu'il rencontre à Paris en 1691, on doit à Johann Bernoulli d'importants travaux et résultats en calcul différentiel et intégral qu'il introduisit en France par l'intermédiaire de Guillaume de L'hospital.
➔ Ce dernier sera le premier à utiliser (1696) le terme français d'intégrale d'une fonction f pour désigner la fonction F dont la différentielle est f(x)dx. Le terme provient du calculus integralis utilisé par Johann et son frère. On parle aujourd'hui, depuis Lagrange, de primitive, plus précisément de fonction primitive. L'intégrale désignant aujourd'hui le nombre :
En 1695, Johann obtint une chaire de mathématiques à l'université de Groningue (Groningen, Hollande). On lui doit dès cette époque, avec son ami Leibniz, les premières études des fonctions exponentielles (appellation due à Leibniz) qui furent développées par son frère Jacques et parachevées par Euler. A la mort de Jakob (1705), sa chaire à l'université de Bâle lui sera confiée.
La fonction exponentielle selon Euler : »
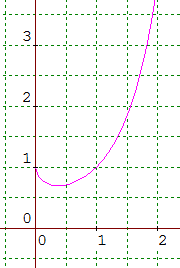En sciences physiques, on lui doit la notation g pour désigner
l'accélération de la pesanteur. Dans ce contexte mécanique, il s'oppose durement aux
idées de Newton en prônant des idées
cartésiennes (théorie des tourbillons, ou
vortex, expliquant l'attraction à distance) retardant le développement de la
mécanique newtonienne sur le continent.
Avec Johann Bernoulli, on entre dans l'analyse fonctionnelle avec la notation fx pour désigner l'image par une fonction f d'un nombre x, qui se "modernisera" par f(x) avec Clairaut et Euler. Là encore, le terme fonction (du latin functio) est de son ami Leibniz. Il en donne cependant une définition très claire en 1718 (Tome second des œuvres complètes, page 235, » réf.2) :
∗∗∗
Johann Bernoulli fut le premier à donner un sens à
l'écriture f(x) = xx.
Quel est son domaine de définition ?
Exprimer f(x) au moyen de moyen de la fonction exponentielle de base e.
Calculer sa dérivée.
Rep : Df =
R+-{0}, f(x) = exlnx, f '(x) = (1 + lnx)exlnx
Johann établit (1701) la méthode de décomposition des fractions rationnelles en éléments simples (qu'utilisèrent cependant également Leibniz et Cotes sur des cas précis). Cette technique fondamentale permettra de calculer des primitives et des intégrales jusqu'ici "inaccessibles".
| Les séries harmonique & semi-harmonique : |
Jean Bernoulli prouva la divergence (la somme est infinie) de la série harmonique (mais l'italien Pietro Mengoli avait déjà obtenu cet important résultat dans les années 1650) :
La suite (un) de terme général, un = 1/n est également dite harmonique. Elle est liée à la musicologie (théorie musicale) issue des premières études de Pythagore sur la fréquence des notes de musique. Le terme harmonie est dérivé du grec harmonia qui signifiait, en menuiserie et architecture, cheville, assemblage et, par là, ce qui est bien ajusté (harmonieux...)
Chaque somme partielle de rang k est appelé nombre harmonique; on a successivement :
1 , 1 + 1/2 , 1 + 1/2 + 1/3 , 1 + 1/2 + 1/3 + 1/4 , ...
Euler étudia également cette série divergente, ce sera la naissance de la célèbre constante d'Euler :
ln
n
=ln(n) désignant le logarithme népérien de l'entier n.
∗∗∗
On
peut se poser la question de savoir si les sommes partielles passent
par des valeurs entières, c'est à dire :
existe-t-il des nombres
harmoniques entiers :
Valeurs entières éventuelles
de la série harmonique
Notons que la série harmonique alternée, également appelée semi harmonique :
est convergente (sa limite est ln 2, logarithme népérien de 2) :
| Le brachistochrone : |
C'est à Jean Bernoulli que l'on doit le célèbre problème (1696) du brachistochrone (du grec brakhus = court et khronos = le temps), dont la solution est un arc de cycloïde.
➔ Pour en savoir plus :
Généalogie des Bernoulli et leurs travaux, une page très
intéressante de P. Radelet de Grave :
http://www.apprendre-en-ligne.net/blog/docu/LesBernoulli.pdf
Œuvres complètes de Jean Bernoulli (en français), tome 2 : https://books.google.be/books?id=10EiPJr29RUC
De Moivre