ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
|
 Fractions continues &
meilleure approximation
rationnelle
» programme JavaScript de développement en fraction continue et recherche de solutions dans les équations de Pell |
 |
On dit souvent maintenant fractions continuées (de l'anglais continued fractions), cela fait plus "tendance"... et/ou cela peut éviter une confusion avec la notion de continuité si la fraction dépend d'une variable. Mais, quitte à faire ringard, j'utiliserai ici l'appellation que m'ont transmise mes professeurs et nos illustres mathématiciens français ou allemands (Lagrange, Legendre, Hermite, Euler, ...). |
De tout temps les mathématiciens ont voulu donner des approximations rationnelles des nombres qu'il manipulaient, comme les radicaux ou le nombre π. Les premiers usages d'approximation par fraction continue se rencontrent chez Aryabhata, Chuquet puis Wallis auquel on doit, semble-t-il, l'appellation.
Huygens, était intéressé par le sujet pour la construction d'horloges astronomiques de grande précision car outre ses applications en algèbre et en analyse, un exemple pratique de l'usage des fractions continues est la recherche d'un ratio simple dans les problèmes d'entraînement par courroies ou par engrenages. Wallis recherchera des critères de convergence (J. Wallisii Opera Mathematica, 1697-1699). Euler (De Fractionibus Continuis Dissertatio, 1737/1744), Lagrange, Gauss, Lambert, Legendre, Hermite, Stern, Hurwitz prendront la relève.
Illustrons le concept par un exemple : nous savons que π = 3,1415926535... et nous voulons en donner des approximations rationnelles de plus en plus précises. Étudions les différentes approximations successives suivantes :
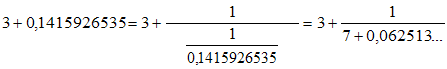
Ainsi π est environ égal à : 3 + 1/7 = 22/7, soit 3,1428... Poursuivons :
Ainsi π est environ égal à : 3 + 1/(7 + 1/16) = 355/113, soit 3,1415929....
Ces deux premières approximations fractionnaires sont, respectivement, celles d'Archimède et de Métius. On peut voir apparaître là un algorithme : soit x un nombre réel positif quelconque de partie entière E(x).
Posons :
e1 est compris entre 0 et 1 et par suite 1/e1 > 1.
On peut donc écrire 1/e1 = q2 + e2 = E(1/e1) + e2 avec e2 = e2 = 1/e1 - E(1/e1) compris entre 0 et 1 ;
Ce qui permet de calculer 1/e2 = q3 + e3 ;
etc.
C'est une méthode d'anthyphérèse. Les ei sont des intermédiaires pour le calcul des qi , dits quotients incomplets, qui sont les entiers constituant l'écriture rationnelle approchée. On a, par exemple, pour la décomposition de π ci-dessus, q1 = 3, q2 = 7, q3 = 15, q4 = 1 :
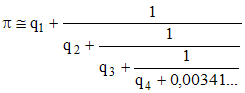
D'une façon générale, le processus conduit à :
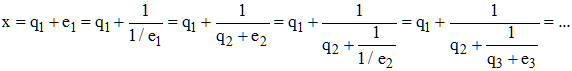
Les relations de récurrence sont, par construction :
en+1 = 1/en - E(1/en) et qn+1 = E(1/en)
Au rang n, nous aurons :
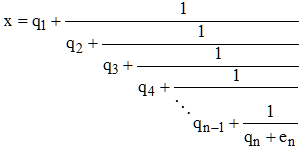
Connaissant les qn, il s'agit maintenant d'établir les relations de récurrence permettant de calculer les an et les bn correspondant à l'approximation rationnelle fn = an/bn du nombre x étudié, appelée réduite de rang (ou d'ordre) n. La suite des quotients incomplets qn conduisant à la fraction fn est souvent notée entre crochets : [q1, q2, ... , qn].
Reprenons notre exemple de x = π :
La réduite d'ordre 4 est :
Étudions les relations entre les an et les bn. On a successivement :
- π ≅ E(p) = q1 = a1 / b1 ,
- π ≅ q1 + 1/q2 = a2 / b2
- π ≅ q1 + 1/(q2 + 1/q3) = a3 / b3
Il apparaît ainsi que :
- q1= E(x) , a1 = E(x) , b1 = 1 , a2 = q1q2 + 1 , b2 = q2
- a3 = q1q2q3+ q1 + q3 , b3 = q2q3 + 1 , d'où :
Par construction du processus, on a finalement :
|
Tant que les ek sont non nuls, k = 1, 2, ..., n (» voir ici le cas en = 0) :
(r1) : ∀n ≥ 1, qn+1 = E(1/en) , en+1 + qn+1= 1/en avec e1 = x - E(x) Et on vérifie par récurrence, en posant ao = 1, a1 = E(x), bo = 0, b1 = 1, que pour tout entier n ≥ 2 : |
Preuve : Par construction, (r2) est vérifiée pour n = 2 et n = 3. Supposons (r2) vraie jusqu'au rang n, n ≥ 3. On remarque que si fn = an / bn = [q1, q2, ... qn-1, qn], alors fn+1 = an+1 / bn+1 = [q1, q2, ... , qn-1, qn, qn+1] peut être obtenu au moyen de fn en remplaçant, dans l'écriture de x, qn + en par qn + 1/(qn+1 + en+1) :
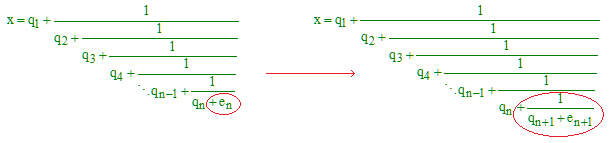
On en déduit :
an+1 / bn+1
= [(qn + 1/qn+1)an-1 + an-2] /
[(qn + 1/qn+1)bn-1 + bn-2]
= [qn+1(qn.an-1 + an-2) + an-1]
/ [qn+1(qn.bn-1 + bn-2) + bn-1]
= (qn+1.an + an-1) / (qn+1.bn
+ bn-1).
| L'étonnante constante de Khintchin : |
En 1934, le mathématicien russe Alexandre Iakovlevitch Khintchin (1894-1959) a montré que pour tous les irrationnels x, à l'exclusion de certains précisés ci-après, de développement x = [q1, q2, ... qn-1, qn], la moyenne géométrique des qi :
(q1×q2×...×qn-1×qn)1/n
converge pour n infini vers une constante K indépendante de x :
K ≈ 2,6854520010652064453... » Source : N.J.A. Sloane, https://oeis.org/A002210 | » voir aussi réf.8
Les exceptions sont :
les irrationnels à développement périodique comme √2, √3, √5, ...
Le nombre e, base des logarithmes népériens.
Les irrationnels de la forme a + b√n où a
et b sont rationnels et n irrationnel de développement périodique.
Il en est
ainsi du nombre d'or Φ.
Plus généralement, les irrationnels éléments d'ensemble de mesure nulle (au sens de la théorie de la mesure).
La formule ci-dessous exprime K sous la forme d'un produit infini :
➔ Le nombre π et la constante d'Euler ne semblent pas faire partie des exceptions mais ce n'est pas prouvé. L'incertitude est également présente sur K lui-même dont on ne sait toujours pas s'il est irrationnel voire transcendant ! En 1995, le mathématicien et informaticien américain David H. Bailey (1948-) calcula plus de 7300 décimales de K.
|
Développement périodique et irrationalité : |
Les relations ci-dessus furent obtenues par Lagrange (1774) cherchant à résoudre l'équation de Pell. Avant lui, Euler démontra que si la suite des quotients d'une fraction continue est périodique, le nombre approché est un irrationnel quadratique, c'est à dire de la forme a + b√n où a, b et n sont des entiers, n n'étant pas un carré. Lagrange prouva la réciproque. Par exemple, √2 est de période 2 car :
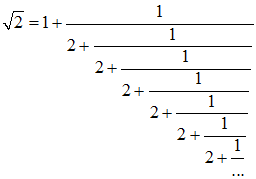
♦ Celle de √3 est 2 puisque √3 = [1 , 1 , 2 , 1 , 2 , 1 , 2 , ...] :
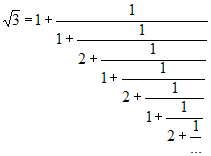
♦ Celle de √5 est 1 puisque √5 = [2 , 4 , 4 , 4 , ...] :
Solutions de l'équation de Pell : »
♦ Quant à celle du célèbre nombre d'or Φ, sa période est 1, le développement étant, superbement :
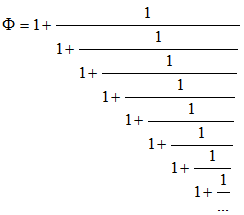
» on peut contrôler ces résultat en utilisant le programme ci-dessous ∗∗∗ Un autre exemple
Propriétés et résultats fondamentaux :
♦ 1/ Si le nombre x étudié est rationnel, alors la suite des réduites est finie : cela se produit dès que en = 0
(» preuve 1). La réciproque de cette assertion fut prouvée par Lambert dans sa preuve de l'irrationalité de π.Par contraposition, on déduit de 1/ :
♦ 2/ Un développement infini indique un x est irrationnel.
➔
Rappelons que tout nombre rationnel r admet un développement décimal fini (cas r = n/10p, n et p entiers, comme 2,34768 = 234768/105) ou infini périodique (comme 7/11 = 0,636363...).» Développement décimal périodique
♦ 3/ La suite des réduites, de terme général fn = an/bn , converge vers le nombre x étudié et les fn sont irréductibles.
♦ 4/ Legendre et Lagrange montrèrent que si x est irrationnel (développement infini), on a :
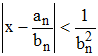
ce qui entraîne la convergence vers x des fn. »
preuves 2 & 3♦ 5/ On a vu au passage dans la preuve précédente que l'on a bn ≥ n - 1 et par suite,
|x - an/bn| < 1/(n - 1)2
Ce qui prouve une convergence vers x relativement rapide (en 1/n2) de la suite de fractions an/bn. Cette convergence est alternée : x - an/bn est du signe de (-1)n+1 et la suite |x - an/bn| converge vers 0 en décroissant.
» preuve 4♦ 6/ A précision égale, il n'existe pas d'approximation rationnelle plus simple (dont les termes seraient plus petits) que celle obtenue par le développement en fraction continue.
♦ 7/ Il fut prouvé (source EDM) que sur 2 réduites consécutives, l'une au moins approche x de sorte que :
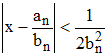
et Borel montra que sur 3 réduites consécutives, l'une au moins approche x de sorte que :
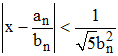
♦ 8/ Inversement, si pour un x irrationnel, Legendre prouva que s'il existe une fraction irréductible a/b tel que
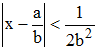
alors a/b est une des réduites du développement de x en fraction continue.
♦9/ Dans le cas d'un nombre x irrationnel du second degré, le développement étant périodique, la suite des quotients incomplets est bornée. Lagrange remarque alors que l'on peut trouver une infinité de rationnels a/b pour lesquels :
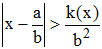
où k(x) désigne une constante ne dépendant que de x.
On doit à Liouville (1844) la généralisation de ce résultat à un nombre algébrique de degré p quelconque (on remplace b2 par bp). Il eut alors l'intuition qu'il était possible de construire des "nombres" pour lequel k(x) n'existe pas : ce seront les nombres transcendants, ainsi débusqués, dits alors nombres de Liouville : on admettait leur existence en tant que partie complémentaire, dans R, des nombres algébriques, mais aucun n'avait été explicité jusqu'alors.
| Programme JavaScript : |
! Attention aux erreurs d'arrondi de l'ordinateur dès que l'on dépasse sa capacité de traitement (chiffres significatifs sous JavaScript). Le programme peut servir à fournir des valeurs fractionnaires simples de résultats numériques issus d'un autre programme :
Par exemple 0.1578947
(7 décimales) sera reconnu comme égal à 2/13 à 0,004 près et comme égal à
3/19 à 10-7
près, ce qui est logique
vu que 3/19 = 0,153846154...
Dans le cadre de l'équation de Pell, si vous recherchez un réduite p/q de √A telle que p2 - Aq2 = d, d entier, D < √A, dites-le au programme...
Dans
le cas d'un entraînement par poulies ou engrenages, si le
ratio
calculé doit être, par exemple, de 3.478, soit 1739/500 le programme fournit,
entre autres possibilités optimales (numérateur et dénominateur les plus
faibles possibles eu égard à a précision souhaitée) : 80/23. Cela signifie qu'il
sera optimal de choisir des poulies de diamètres respectifs 80 mm et 23 mm. Pour des engrenages
(entraînement direct ou à chaînes) la solution 167/48 (respectivement 167 et
48 dents) pourra être utilisée.
Expressions comprises :
➔
Un nombre décimal doit être entré avec le point décimal et non la virgule, sinon il est traité à l'américaine comme un entier...π (entrer pi), e (base des logarithmes népériens, entrer tout simplement e) et Φ (nombre d'or : entrer phi) sont compris par le programme, ainsi que les fonctions mathématiques comme : sqrt(5) pour la racine carrée de 5, (1+ sqrt(5))/2 pour le nombre d'or, log(2) pour le logarithme népérien de 2, etc.
! Les erreurs d'arrondi, au-delà de 16 chiffres significatifs peuvent gravement dégrader la suite des quotients incomplets. Exemples avec le nombre d'or ou la racine carrée de 3.
» JavaScript & fonctions mathématiques
|
<SCRIPT LANGUAGE=JavaScript> |
➔ Pour en savoir plus (Ctrl + Clic = Nouvel onglet) :
,
Jean
Dieudonné et une équipe de mathématiciens
»