
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Pour tout x > 0, l'intégrale :

est convergente.
Preuve : la limite en 0 de e-t est 1, donc au voisinage de 0, on a e-ttx-1 ~ tx-1= 1/t1-x dont l'intégrale converge en 0 pour 1 - x < 1, soit pour x > 0. Pour x infiniment grand positif, on peut utiliser que, pour tout réel α et t > 0 suffisamment grand, tα < et/2 (passer aux log et utiliser ln(t)/t tend vers 0). En conséquence, pour t suffisamment grand, e-ttx-1 < et/2 dont l'intégrale est convergente (» intégrale généralisée).
Ces considérations montrent que l'intégrale converge uniformément sur ]0,+∞[. On pose alors :
![]()
Dérivation :
Par dérivation sous le signe somme et par un raisonnement par récurrence, on peut montrer que Γ est de classe C∞ (infiniment dérivable) et :
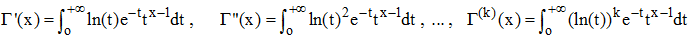
Lien avec la fonction factorielle :
Si x est entier naturel n, alors :
Preuve : on procède par intégration par parties :
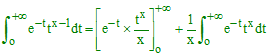
Ce qui fournit, par passage à la limite, la relation Γ(x + 1) = xΓ(x). Mais Γ(1), intégrale de e-t sur ]0,+∞[ n'est autre que 1. D'où le résultat annoncé.
➔ On remarque au passage l'intéressante relation, valable pour tout x > 0 :
Γ(x + 1) = xΓ(x)
i Eu égard à l'aspect factorielle, donc produit, Gauss préféra noter Π ("grand pi") la fonction x → Γ(x + 1) conduisant alors à Π(x) = x! pour x entier. D'autant que ce dernier est à l'origine de la notation Π pour un produit comme Πai pour désigner le produit a1a2a3... Dans le même ordre d'idées on doit le Σai = a1+ a2+a3... à Euler.
∗∗∗
En appliquant cette relation, montrer que si p est un entier : x(x + 1)(x + 2)...(x + p - 1) =
Γ(x + p)/Γ(x)
Séries hypergéométriques : »
Noter que Γ admet un développement asymptotique (| x | "grand"). Voici les 4 premiers termes :

Correction de la formule de Stirling : »
| Formule de Legendre-Gauss pour la fonction Γ : |
Legendre a démontré la formule :
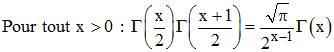
Vu que Γ(1) = 1, on peut déduire de cette formule que Γ(1/2) = √π.
Gauss en a donné une forme généralisée où la précédente en est le cas particulier n = 2 :
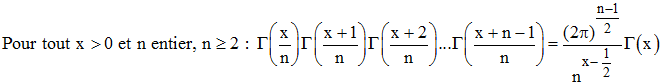
| Formule d'Euler-Gauss pour la fonction Γ : |
 »
Gauss
»
Gauss
| Formule des compléments et calcul de Γ(n + 1/2) : |
Euler démontra la formule des compléments : si 0 < p < 1 , alors :
Conséquence, si p = 1/2 :
C'est l'intégrale dite de Gauss. Elle nous conduit, en utilisant la récurrence Γ(x + 1) = xΓ(x), à :
| Formule de Weierstrass pour la fonction Γ de Euler : |
Weierstrass s'intéressa non seulement aux développements en série des fonctions, sommes infinies de type Σanfn(x), mais aussi sous forme de produits infinis Πanfn(x). Un exemple qui porte son nom est le développement de la fonction gamma Γ :
où γ désigne la constante d'Euler, limite pour n infini de 1 + 1/2 + 1/3 + ... +1/n - ln n. La preuve de la formule est simple si l'on part de celle d'Euler :

On utilise un petit artifice :
nx = exln n = exln n × e-x - x/2 -... -x/n × exex/2...ex/n = ex(ln n -1 -1/2 -... -1/n) × exex/2...ex/n
En passant à la limite, on voit apparaître - γ dans la ( ) de l'égalité ci-dessus. Or n! = 1 × 2 × 3 × ... × n. Le quotient n!/[x(x + 1)...(x + n)] peut alors s'écrire : 1/x × (1 + x/1)(1 + x/2)...(1 + x/n). D'où Γ(x) est la limite pour n infini de :

ce qui conduit à la formule annoncée.
| Cas complexe : |
Si z désigne le nombre complexe x + iy, l'intégrale généralisée :
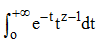
est absolument convergente pour tout z tel que x = Re(z) > 0. En effet, à la manière du cas réel, on a ici, en module : |e-ttz-1| = e-ttRe(z)-1| = e-ttx-1. On définit donc ainsi une fonction encore notée Γ :
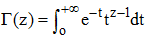
Mais l'intérêt de passer dans le champ complexe réside dans le prolongement de l'existence de Γ pour des valeurs de z non réduites au demi-plan Re(z) > 0. Pour cela, on écrit :

et on remplace e-t par son développement en série entière :

cette série converge uniformément en tout t de [0,1]. Par intégration terme à terme, on obtient sans difficultés :

car l'intégrale du membre central des égalités ci-dessus égale 1/(n+z). Dans tout disque D du plan complexe ne contenant aucun entier négatif ou nul, le critère de Weierstrass indique que la série obtenue ci-dessus converge uniformément : en effet, en module, le terme général est 1/(n + z)n! et on est alors assuré, dans chaque disque D, de l'existence d'un réel k > 0 tel que |n + z| > k, ce qui assure la convergence de la série majorante de terme général 1/kn!
Finalement, la fonction définie ci-dessous est encore notée Γ. Elle apparaît en effet comme le prolongement à C \ Z- du cas réel (x > 0) ou complexe restreint à Re(z) > 0 :

∗∗∗
Vérifier que le prolongement de Γ ci-dessus vérifie
encore :
Γ(z + 1) = Γ(z)
Indication : écrire
Γ(z + 1), intégrer par parties la quantité intégrale et utiliser un petit
artifice dans l'expression de la série
Lien entre les fonctions Γ et ζ de Riemann : »
➔ Pour en savoir plus :
Cours de mathématiques,
tome II,
par Jean Bass,
Éd. Masson et Cie - Paris, 1964.
Théorie des fonctions par Georges Valiron, La fonction Γ : pages 169-174, Éd. Masson, 1942.
Étude de la fonction Gamma par
Abdellah Bechata :
http://abdellah.bechata.free.fr/telechargement/gamma/pdf/gamma.pdf
Traité des fonctions elliptiques et des intégrales eulériennes,
Adrien
Legendre sur Google Livres :
https://books.google.fr/books?id=wy7vAAAAMAAJ (Tome 2, intégrales
eulériennes)