ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 MAYER Johann Tobias,
allemand, 1723-1762 |
Passionné
d'architecture, son père lui enseigna les mathématiques et dès l'âge de
16 ans, le jeune Johann présentait des plans de fortifications militaires. Deux
ans plus tard, il publiait des résolutions de problèmes géométriques ardus.
En 1746, Mayer travaille au service cartographique de Nuremberg et se spécialise en astronomie. Il sera professeur à Göttingen (1750) et nommé directeur de son célèbre observatoire (1754).
Mayer établit des tables des cycles lunaires et évalua les erreurs dues aux imperfections des réglages des instruments de mesure. En 1748, il utilisa pour la première fois, à la manière d'Euler à la même époque dans l'étude des orbites de Saturne et de Jupiter, mais indépendamment de lui, une méthode d'ajustement pour étudier la position d'un point sur la Lune :
| Droite de Mayer (statistique) : |
La méthode d'ajustement linéaire de Mayer, dite des moyennes discontinues ou des moyennes mobiles, consiste à partager, de façon pertinente, un nuage statistique de k × n points rangés dans l'ordre de leurs abscisses, par k points : chaque n-uplet (x
i,yi) de points consécutifs étant remplacés par leur moyenne, point dont les coordonnées sont les moyennes arithmétiques de ces points. Ce type d'ajustement permet de corriger les fluctuations entre mesures rapprochées : séries chronologiques notamment (variations saisonnières).
➔ Plus généralement, si le nombre de points est un entier premier, 19 par exemple, on peut choisir 2 groupes de 6 points et un groupe de 7 ou 5 groupes de 3 points et un groupe de 4. C'est là que la pertinence des groupements doit jouer son rôle.
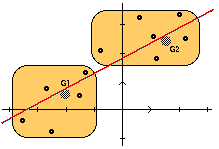
Lorsque k = 2, (2n points), on obtient la droite de Mayer définie dans ce cas par les deux points moyens partiels G1 (1 ≤ i ≤ n) et G2 (n + 1 ≤ i ≤ 2n), à savoir :
Dans le cas d'un nombre impair de points, de la forme 2n + 1, on procède de même en choisissant cette fois les groupements G1 (1 ≤ i ≤ n) et G2 (n + 1 ≤ i ≤ 2n + 1) ou bien G1 (1 ≤ i ≤ n + 1) et G2 (n + 2 ≤ i ≤ 2n + 1).
Propriété :
Le point moyen G n'est autre que l'isobarycentre des points du nuage considéré. En utilisant la propriété d'associativité du barycentre, on en déduit que G est aligné avec G1 et G2 :
Quels que soient les regroupements, la droite de Mayer pour N points
passe par le point moyen du nuage G(Σ1 ≤ i
≤ N xi /N, Σ1
≤ i ≤ N yi /N)
Méthode, dite des moindres carrés : »
∗∗∗
1. - Le nombre de candidats à un concours de la fonction
publique a évolué de la façon suivante :
| Année | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| Nombre de candidats | 1170 | 1139 | 1023 | 980 | 942 | 847 | 716 |
a) Représenter le nuage de
points M(xi,yi)
où xi est le rang de l'année (xo = 0 pour 1997)
et yi
le nombre de candidats correspondant.
b) Ajuster
linéairement le nuage par la méthode de Mayer.
c) Quel est le nombre
prévisible de candidats pour l'année 2004 ? Remarque ?
☼
2. - Le tableau statistique ci-dessous indique l'allongement y
d'une barre métallique soumise à une augmentation
de température x exprimée en degrés Celsius :
|
x° |
10 | 20 | 30 | 40 | 50 | 60 |
|
allongement y |
1 | 3 | 4 | 5 | 7 | 8 |
a) Vérifier graphiquement
une corrélation linéaire entre x et y.
b) Ajuster le nuage par la méthode de Mayer
en subdivisant le nuage en deux groupes convenables. Remarque ?
c) Quel est
l'allongement prévisible pour une augmentation de température de 54° ?
Rép : G1(20;8/3) , G2(50;20/3) ,
(d) : y = 2x/15 (ou bien : 2x - 15 = 0).
La droite passe par l'origine : logique car
si x = 0, l'augmentation de
température est nulle, donc la barre conserve sa longueur initiale.
c) si x = 54, on a y = 108/15,
soit y = 7,2 cm.
Extrait Bac A2-A3 - Abidjan 1990
Corrélation linéaire : » Statistique élémentaire : » Statistique à deux variables : »
Lambert