
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» géodésique | éléments différentiels | surfaces "classiques" et leurs équations | surfaces réglées | surfaces et variétés | plan dans lespace |

Au 19è siècle, on avait déjà de l'humour... : un dessin de Cham, caricaturiste
français (1819-1879) Encyclopédie Larousse méthodique (1955) →
Généralités :
En dehors de l'acception courante, synonyme d'aire (en toute rigueur une aire est la mesure d'une surface), la notion mathématique de surface en tant qu'ensemble de points de l'espace (assimilé à R3), est fort complexe.
➔ Écoliers, collégiens, noter d'ores et déjà que surface ne signifie nullement plat. Une feuille de papier est une surface, elle le reste si elle est chiffonnée !
La théorie des surfaces a été tout particulièrement étudiée par Monge en France, puis Gauss et Riemann en Allemagne, ce dernier se dégageant de l'aspect purement euclidien. Elle relève de la géométrie différentielle (usage du calcul différentiel, des dérivées partielles) dans l'étude des formes, des courbures, de l'orientation dans un repère donné.
On peut concevoir une surface de différentes manières :
| Surface en tant que limite qu'occupe un objet 3D de l'espace : |
 La surface est alors sa frontière, en quelque sorte entre son intérieur et son extérieur :
La surface est alors sa frontière, en quelque sorte entre son intérieur et son extérieur :
•
Une
sphère
en tant que limite du volume occupée par une boule, est une
surface close qui n'a pas de bord. On ne peut
pas passer de l'extérieur à l'intérieur (et vice versa) sans la trouer, ce qui
la transformerait en surface à bord et en changeant, ce que l'on appelle son
genre.
•
Un bol de petit
déjeuner "infiniment mince" est une
surface à bord
(un cercle) s'interprétant comme une demi-sphère. Un insecte plat
unidimensionnel pourrait passer continûment de l'intérieur à l'extérieur.
 Contrairement
à la sphère, une telle surface est non considérée comme close car les
voisinages (au sens topologique) de tout point du bord admettent des points non
inclus sur le bol mais dans le bol : et c'est heureux car cela
permet de remplir le bol...
Contrairement
à la sphère, une telle surface est non considérée comme close car les
voisinages (au sens topologique) de tout point du bord admettent des points non
inclus sur le bol mais dans le bol : et c'est heureux car cela
permet de remplir le bol...
• Un plan dans l'espace est une surface... plane. Un plan dans le plan est le plan, c'est à dire l'espace dans lequel on peut rencontrer des surfaces comme un disque :
• Un disque du plan, sans trou, par exemple d'équation x2 + y2 ≤ 1 (disque unité), est une surface dont le bord, qui le délimite, est le cercle unité d'équation x2 + y2 = 1.
Le même disque en suspension dans l'espace, par exemple d'équation x2 + y2 ≤ 1, z = 1, est une surface possédant cette fois 2 "faces". C'est une surface à bord. Comme pour le bol ci-dessus, un insecte plat unidimensionnel pourra passer continûment du "dessus" au "dessous".
Si maintenant on se limite à x2 + y2 < 1, z = 1, il s'agira d'un disque ouvert (au sens topologique). On parle aussi de surface ouverte. Il n'a plus de bord au sens mathématique :
Surface et variété topologique :
» »
Riemann
»
Riemann
• Une feuille de papier (si son épaisseur est "nulle"...), froissée ou non, représente une surface finie.
• Le
cylindre
ou le cône
sont des surfaces ouvertes illimitées. Les représentations finies (tronquées)
que l'on en donne sont des surfaces à bord.
• La "surface" d'une chambre à air, d'une
bouée : assimilable à un
tore est une surface close (tant qu'elle n'est pas crevée...).

Équation de surfaces usuelles : »
Les acceptions intuitives données ci-dessus (surface close, surface à bord) peuvent cependant induire en erreur : le célèbre ruban de Möbius n'a ni "dessus" ni "dessous" et Klein a su exhibé une surface close, s'interprétant dans R4, bouteille de Klein, n'ayant ni intérieur ni extérieur.
La théorie des surfaces est en fait très complexe et est à l'origine de la topologie. En topologie algébrique (et différentielle) et depuis les travaux de Poincaré et de Fréchet sur le sujet, les surfaces s'interprètent comme des variétés topologiques connexes et compactes dont chaque point admet un voisinage homéomorphe à un ouvert de R2 (surface close) ou de R × R+ (surface à bord).
Les surfaces closes sont également fermées au sens topologique du qualificatif. Les surfaces à bord aussi mais elles se distinguent des surfaces closes dans lesquelles tout voisinage de tout point y est entièrement inclus.
Une variété topologique connexe non compacte dont chaque point admet cependant un voisinage homéomorphe à un ouvert de R2 est dite ouverte. Dans le plan, ce serait le cas du disque d'équation x²+y² < 1.
| Surface obtenue par rotation d'une courbe autour d'un axe : |
Une courbe plane en rotation autour d'un axe engendre un volume dont on peut représenter la surface dite alors de révolution. Ci-dessous, à droite, la surface en forme de "bol" est engendrée par la rotation autour de l'axe des ordonnées d'un segment de courbe d'équation y = x3 sur l'intervalle [0;1].

Le caténoïde ci-dessous en est un bel exemple. C'est aussi une surface minimale :
| Surface obtenue comme enveloppe d'une famille de droites (surface réglée) : |
Une droite de l'espace (dite génératrice) se déplaçant continument en s'appuyant sur au moins une courbe fixe (pouvant être une droite), suivant une loi précise, engendre une surface, on parle de surface réglée.
Exemple :
L'hyperboloïde à une nappe : quadrique (surface algébrique de degré 2) d'équation générale :
x2/a2 + y2/b2 - z2/c2 = 1

L'hyperboloïde à une nappe en tant que surface (doublement) réglée : »


Centrale
nucléaire de Tricastin (Drôme)
et châteaux
d'eau aux environs aux environs de l'aéroport de Roissy (France)
Surface réglée cylindrique, conique, conoïde :
Une surface réglée est dite cylindrique lorsque les droites génératrices conservent une même direction, conique lorsque les génératrices passent par un point fixe et conoïde lorsque les génératrices s'appuient sur une droite fixe (axe) et sur une seconde courbe directrice fixe (c) en restant parallèles à un plan donné (plan directeur).
Quelques exemples :
Le cylindre (resp. le cône) est obtenu par une une droite s'appuyant sur un cercle (c) tout en gardant la même direction : celle de son axe passant par le centre du cercle (resp. en passant par un point fixe : le sommet).
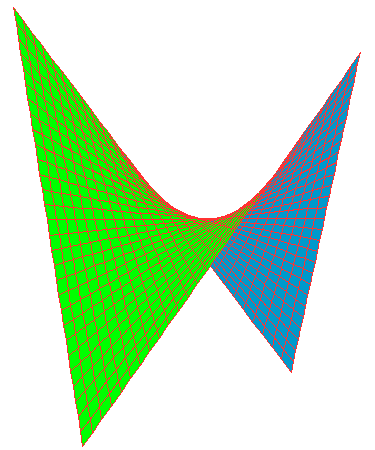
Le paraboloïde hyperbolique, ci-dessous, (c) est une droite, et le coin de Wallis, (c) est un demi-cercle, sont des surfaces conoïdes.
Le parapluie de Whitney est un conoïde s'appuyant sur une parabole.
Le conoïde de Plücker s'appuie sur une sinusoïde tracé sur un cylindre.
➔ Une surface réglée doit pouvoir être exprimée au moyen de l'équation d'une famille de droites ou segments de droites, c'est à dire d'une fonction φ de R2 dans R3 du type :
(u,v) →φ(u,v) = f(u) + v.δ(u) , (u,v)∈ I × J ⊂R2
où δ(u) est une direction de droite, c'est à dire un vecteur fonction de u.
Sous cette forme, dans le cas des conoïdes, lorsque u décrit I, u→ f(u) définit pour chaque v fixé, une courbe paramétrée (cv) de l'espace sur laquelle s'appuie l'ensemble des génératrices.
Le paraboloïde hyperbolique (équilatère) ci-dessus d'équation z = xy, également appelé selle de cheval pourra être défini paramétriquement par φ(u,v) = (u,0,0) + v(0,1,u), ensemble des droites passant par (u,0,0) du plan (xOy) et dirigées par δ(u) de coordonnées (0,1,u), c'est à dire :
x = u , y = v , z = uv
Plus généralement, l'équation cartésienne de cette quadrique est de la forme z = x2/a2 - y2/b2. Lorsque a = b, en posant X√2 = x - y, Y√2 = x + y (rotation du plan xOy de π/4 autour de Oz), on se ramène à z = 2XY/a2.
Selle de cheval et indicatrice de Dupin : » Conoïde de Plücker : »
| Surfaces développables & surfaces réglées : |
Des surfaces comme le cylindre ou le cône sont dites développables : intuitivement, on peut en obtenir le "patron" sur un plan sans déformation, déchirure ou boursouflure. Elles furent étudiées par Monge et son élève Lancret.
Dans son cours Application de l'Analyse à la géométrie (1807) à l'usage des élèves de l'École Polytechnique, Monge écrit en introduction aux surfaces développables (§12) :
Les surfaces développables sont celles qui, étant supposées flexibles et inextensibles, sont de nature à pouvoir s'appliquer sur un plan au moyen d'une simple flexion, et le toucher alors dans tous leurs points, sans rupture et sans duplicature.
Notion (distincte) de surface applicable : »
! Toutefois, une surface réglée, donc réunion d'une infinité de droites, n'est pas pas toujours développable. La courbure totale (ou courbure de Gauss) d'une surface développable est nulle, ce qui n'est pas le cas d'une surface réglée non développable (courbure totale négative).
Dans le cas général, les surfaces développables s'obtiennent comme enveloppes d'une famille de plans. En chaque point d'une génératrice le plan tangent ne varie pas : ce qui n'est pas le cas, par exemple, de l'hyperboloïde et du ruban de Môbius qui ne sont donc pas développables ce que l'on vérifiera facilement avec le critère énoncé ci-après.
Une surface développable peut rouler sur un plan, le contact se faisant d'une génératrice à une autre : cas du cylindre par exemple ou du cône. On peut maintenant donner une définition pratique et opérationnelle d'une surface développable dont on connaît l'équation :
Les surfaces développables sont les surfaces régulières et réglées, le plan tangent ne variant pas le long d'une génératrice
Une surface développable apparaît ainsi comme ensemble des tangentes à une courbe gauche régulière dont tous les points sont réguliers (admettant une tangente en chacun de ses points).
∗∗∗
Une feuille de papier chiffonnée (mais non déchirée)
est-elle développable ?
☼
La sphère et l'ellipsoïde ne sont ni réglées, ni développables. Le tore ne l'est pas non plus : si vous le sectionnez comme on le ferait pour une chambre à air ou une saucisse sèche, vous n'obtiendrez pas un cylindre car si tel était le cas, avec les notations ci-dessous, on aurait a = 2r + a ! (la courbure n'est pas la même). Le ruban de Möbius s'interprète comme une portion de surface réglée non développable (sa fabrication au moyen d'une bande de papier n'en est qu'une approximation).
Calcul des courbures moyenne et totale en un point d'une surface : »
Surface réglée des tangentes :
Il s'agit du cas particulier : (u,v) →φ(u,v) = f(u) + v.f '(u) , v décrivant R, φ étant supposée au moins de classe C2. Les génératrices sont les tangentes en u à la courbe (c) définie par f. ∂φ/∂u = f '(u) + v.f ''(u) et ∂φ/∂v = f '(u). On a donc un souci si v = 0 : point singulier où la normale n'existe plus. La surface réglée des tangentes est une surface développable.
| Les différents types d'équation d'une surface : |
Dans un repère orthonormé (Ox, Oy, Oz) que l'on suppose orthonormé, de plan horizontal xOy, une surface peut être définie de diverses manières. En voici trois :
1/ Équation cartésienne :
Il s'agit, comme pour les courbes du plan (cartésienne est forgé sur le nom de Descartes), d'une relation de la forme :
f(x,y,z) = 0
Par exemple :
L'équation d'un plan est de la forme ax + by + cz + d = 0, a, b et c non tous nuls.
La sphère de rayon R centrée à l'origine a pour équation, dans un repère orthonormé :
x2 + y2 + z2 = R2
! Il s'agit de distinguer sphère et boule. Concrètement, la boule est l'intérieur de la sphère constituant sa surface, et son équation sera ici x2 + y2 + z2 < R2 : la distance de ses points par rapport au centre est inférieure au rayon. Ci-dessous : une boule de quartz, dont l'ombre (perspective plane) est une ellipse : projection d'un disque de la boule passant par son centre.

➔ Ci-dessous, une construction approximativement sphérique à Paris, place de la Défense. En fait, une surface polyédrique (les faces sont quadrilatères, trapèzes pour la plupart). La structure fait apparaître des parallèles (cercles parallèles à l'équateur) et des méridiens (grands cercles passant par les pôles). Un bâtiment sphérique et vitré comme celui de la Défense est souvent appelé géode (du grec gê = Terre et eidos = forme) : ce terme, utilisé en minéralogie, désigne un minéral creux de forme approximativement sphérique dont l'intérieur est cristallisé.

∗∗∗
Cube inscrit dans une sphère ,
petit exo de probabilités..
2/ Équation paramétrique, coordonnées curvilignes :
Ce type d'équation est très employé car très pratique dans l'étude de l'aspect local d'une surface (normale, courbure, plan tangent, ...). On a ici recours à deux paramètres indépendants u et v appelées coordonnées curvilignes et initiées par Gauss : la surface S est définie par une fonction de deux variables φ : (u,v) →φ(u,v), vecteur de R3 de coordonnées
x = f(u,v), y = g(u,v), z = h(u,v).

Avec ce type de coordonnées, la sphère, de centre O, de rayon R a pour équation dans le repère orthonormé direct (O, Ox, Oy, Oz) :
➔ Dans le cas de notre planète assimilée à une sphère, u correspond à la latitude et v à la longitude.
Coordonnées sphériques : » Équation de surfaces "classiques" : » Cas du ruban de Möbius : »
» Trièdre de Ribaucour , Indicatrice de Dupin
3/ Équation par lignes de niveau :
Ce sont des équations cartésiennes du type z = f(x,y), intersections d'un solide avec un plan horizontal de cote z.
Par exemple :
La surface définie par z = xy est un paraboloïde hyperbolique
la surface ci-dessous a pour équation z = sin2x.cos3y :
|
Surface algébrique : |
Une surface est dite algébrique de degré k si son équation peut se ramener à la forme f(x,y,z) = 0 où f est un polynôme de degré k en x, y et z : on entend là que tout monôme de la forme axnymzp vérifie n + m + p ≤ k et au moins un monôme vérifie n + m + p = k.
Un cas élémentaire de surface algébrique de degré 2 est donné par le cône de révolution d'axe Oz, d'équation x2 + y2 = z2tan2α, ou α désigne le demi-angle au sommet :

On appelle quadriques les surfaces algébriques de degré 2. L'étude de telles surfaces peut être grandement simplifiée par la réduction des formes quadratiques associées au moyen de leurs valeurs propres. Un exemple de surface du 4ème degré (quartique) est le conoïde de Wallis :

Cas classiques de surface et leurs équations : »
∗∗∗ Étude d'un cas : quadrique d'équation yz + zx - xy = 1
|
Géodésique d'une surface : |
Pour une surface quelconque (S), par analogie avec les mesures à la surface de la Terre, on appelle ligne géodésique (du grec gê = terre et deiein = diviser, partager) le chemin le plus court entre deux points de (S) : courbe réalisant le chemin minimal entre ces deux points.
Les géodésiques de la sphère sont les arcs de grands cercles : portions de méridiens. La Terre étant assimilée à une sphère, les routes maritimes et aériennes les plus courtes sont celles utilisant une géodésique : chemin orthodromique;
Les géodésiques du plan sont ses droites;
Les géodésiques du cylindre sont de trois types : ses génératrices (droites du cylindre, parallèles à son axe), ses cercles (sections circulaires par un plan perpendiculaire à son axe) ainsi que ses hélices circulaires. Sa courbure n'est pas constante mais il est isomorphe au plan euclidien par développement; on peut donc y utiliser la distance euclidienne par déroulement et réenroulement.
Les géodésiques de la pseudosphère, imaginée par Beltrami, sont des tractrices. Elles correspondent à une courbure minimale.
Pseudosphère et géodésiques (lien externe) : »
En tout point d'une géodésique, le plan osculateur est normal à (S).
» Nonius , Gauss , Lancret , Bonnet , Meusnier , Cassini
Loxodromie, orthodromie : » Triangulation : »
|
Surfaces et géométrie différentielle, plan tangent, normale, courbes gauches : |
Au lycée, on étudie les courbes planes et leurs propriétés locales (extrema, tangentes, asymptotes, etc.) en coordonnées cartésiennes ou paramétriques (Terminale S). On conçoit que ce qui différencie les courbes planes réside dans leurs courbures en chaque point.
Dans l'espace, les choses sont plus difficiles, la courbure d'une courbe en un point n'est pas unique : elle admet une torsion mesurant à changer de plan. L'étude des surfaces nécessitant une bonne connaissance du calcul différentiel. Euler fut le grand initiateur de l'étude des surfaces grâce à l'apport du calcul différentiel et intégral : on parle de géométrie différentielle.
Plan tangent et normale à une surface, point régulier :
Le plan tangent est à une surface ce que la tangente est à une courbe plane :
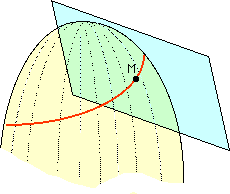
Si l'on trace une ligne quelconque sur une surface, on obtient une courbe gauche pour laquelle la notion de plan tangent en un point coïncide avec celui de la surface au même point. En France, à la même époque que Euler, Clairaut s'intéresse tout particulièrement à ces courbes.
La surface étant définie par une équation de la forme f(x,y,z) = 0, l'équation du plan tangent en un point M(a,b,c) est alors :
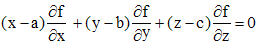 Tangente à une courbe gauche :
»
Tangente à une courbe gauche :
»
➔ Si la surface est définie par ses lignes de niveau, son équation est du type z = f(x,y). On se ramène à la forme ci-dessus F(x,y,z,) = 0 en posant F(x,y,z) = f(x,y) - z avec :
∂F/∂x = ∂f/∂x , ∂F/∂y = ∂f/∂x , ∂F/∂z = -1
Pour un point régulier de la surface, c'est à dire dont les dérivées partielles ∂f/∂x, ∂f/∂y et ∂f/∂z en ce point ne sont pas simultanément nulles, la normale en M(a,b,c) est la perpendiculaire en M au plan tangent. Elle est donc dirigée par le vecteur n(∂f/∂x,∂f/∂y,∂f/∂z). On dira d'une surface dont tous les points sont réguliers, qu'elle est régulière.
Si les 3 dérivées partielles sont nulles (gradient nul), on est en présence d'un point singulier de la surface. Par exemple, dans le cas du cône, le sommet en est un.
Tout comme pour les points doubles d'une courbe, une surface peut se "croiser" elle-même... On parle alors d'auto-intersection. Dans le cas d'une surface paramétrée à la manière de Gauss, x = f(u,v), y = g(u,v), z = h(u,v), cela signifie qu'un même point de la surface est obtenu pour deux couples distincts (u1,v1) et (u2,v2).
Point-pince, singularité de Whitney : »
Dans le cas général, l'équation de la normale est :
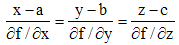 Représentation cartésienne d'une droite de l'espace
:
»
Représentation cartésienne d'une droite de l'espace
:
»
♦ Si la surface est définie par la représentation paramétrée x = f(u,v), y = g(u,v), z = h(u,v), l'équation du plan tangent en M(a,b,c) est fourni par le déterminant (pour simplifier, une dérivée partielle comme ∂f/∂u est notée ci-dessous fu') :
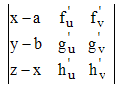
Il s'agit du plan passant par M (1ère colonne) contenant deux tangentes en M dirigées par les vecteurs représentés par les 2è et 3è colonnes.
Remarque importante :
Avec la notation : (u,v) → φ(u,v),
vecteur de R3 de coordonnées x = f(u,v), y = g(u,v), z =
h(u,v), lorsque M n'est pas singulier, les seconde et troisième colonne du déterminant sont respectivement
∂φ/∂u
et ∂φ/∂v,
vecteurs directeurs du plan tangent en M et la normale en M(u,v) est alors
portée par le produit
vectoriel ∂φ/∂u![]() ∧
∧![]() ∂φ/∂v. Pour le calcul d'une
normale unitaire, il faudra penser à la
normer !
∂φ/∂v. Pour le calcul d'une
normale unitaire, il faudra penser à la
normer !
♦ Si la surface est définie par les lignes de niveau z = f(x,y), on se ramène à la forme F(x,y,z) = 0 en écrivant z - f(x,y) = 0. La dérivée partielle par rapport à z est alors -1 et l'équation du plan tangent devient :
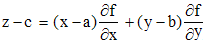
et l'équation de la normale se résume à :
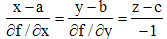
Plan osculateur en un point d'une courbe gauche : » Trièdre de Darboux-Ribaucour : »
|
Genre d'une surface : |
On voit que le tore possède un trou : il est connexe (du latin connexus = d'un seul tenant, participe passé de conectere = attacher ensemble, contraction de cum nectere) mais troué (non simplement connexe). La sphère n'en possède pas : ces deux surfaces n'ont pas le même genre. Les mathématiciens du 19è siècle se sont penchés sur la classification des surfaces basée sur ce concept :
Genre d'une courbe, d'une surface : » Connexité : »
➔ Pour en savoir plus :
Cours de mathématiques, tome 1, Ch. 21 par Jean Bass - Ed. Masson et Cie - Paris, 1964.
COURS DE MATHEMATIQUES.
Tome 3, Géométrie et cinématique, 2è édition,
Ch. VII, par J. Lelong-Ferrand, J.-M. Arnaudiès
Classes préparatoires, 1er cycle universitaire - Dunod Université -
1993.
ABRÉGÉ
D'HISTOIRE DES MATHÉMATIQUES, sous la
direction de Jean Dieudonné
Ch IX, Géométrie différentielle par Paulette Libermann -
Ed. Hermann
ATLAS DES MATHÉMATIQUES, Fritz Reinhardt,
Heinrich Soeder,
Ch. géométrie différentielle
La Pochothèque - Le Livre de Poche (collection
Encyclopédies d'aujourd'hui), 1997
APPLICATION DE L'ANALYSE A LA GÉOMÉTRIE,
Gaspard Monge
Les cours historiques de l'Ecole Polytechnique (1807) -
Ed. MARKETING (ellipses) - 1994
Courbes et Surfaces, Que sais-je ?, n° 564 par Jean Taillé, P.U.F.
Courbes et surfaces par Pierre Lecomte : http://www.geothalg.ulg.ac.be/Courbes_Surfaces.pdf
Très beau site (et très complet) de Robert Ferreol : surfaces et leurs équations dans différents systèmes de coordonnées, mais aussi des courbes 2D, 3D, des polyèdres : http://www.mathcurve.com/surfaces/surfaces.shtml
Tout savoir sur les surfaces, du b-a
ba aux surfaces modulaires, par Henri-Paul de Saint-Gervais, sur le site
Analysis Situs (CNRS) :
http://analysis-situs.math.cnrs.fr/Les-premieres-surfaces-la-sphere-le-cylindre-le-tore.html
Le site de Xah Lee : http://xahlee.org/PageTwo_dir/more.html
Le site de Xiao Gang pour tracer vos propres courbes ou
surfaces, explicites ou paramétrées avec ou sans animation :
http://wims.unice.fr/~wims/wims.cgi?session=XGD2CBA318.3〈=fr&module=tool/geometry/animtrace.fr
• Parmi les logiciels de
Denis Monasse,
un programme
remarquable gratuit, utilisé pour cette page, à télécharger pour tracer de très
belles surfaces paramétrées (en
coordonnées cartésiennes, sphériques ou cylindriques)
: dans la rubrique Logiciels sur Surface2.
Vous pouvez aussi cliquer directement
ici
afin de télécharger le fichier exécutable (type jar) en choisissant ensuite
Ouvrir pour lancer
directement le logiciel de tracé.
