ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

HIPPARQUE de Nicée (ou Hipparque de Rhodes), grec, -190?/-125?           »  projection stéréographique

Hipparque, dit le Rhodien, car la plupart de ses travaux furent écrits à Rhodes, est sans doute le plus brillant astronome de l'Antiquité. On peut le considérer comme le fondateur de la trigonométrie, nouvelle branche des mathématiques (pilier!) que Regiomontanus développera 1500 ans plus tard comme une des branches maîtresses des mathématiques. Le terme trigonométrie tient son nom du grec trigônos = triangle et métron = mesure : pour signifier mesure des angles d'un triangle.

On lui doit les premières tables trigonométriques (par usage des longueurs de cordes) de raison un demi-degré et le premier catalogue d'étoiles : il en recensa 1025 !

Dans ses calculs Hipparque utilisa l'usage du système sexagésimal, c'est à dire à base 60 (dut latin sexagesimus = soixantième) hérité des Babyloniens pour la mesure du temps. Selon certains spécialistes, le mathématicien et astronome Hypsiclès d'Alexandrie, qui vécut 2è siècle avant J.-C., l'aurait également utilisé avant Hipparque.

La mesure du temps des Babyloniens : »            Les systèmes de numération, le système sexagésimal : »

Conforté par Ptolémée et les mathématiciens arabes, cet usage traversa les siècles. C'est ainsi que nous fut léguée la division de la circonférence en 360 degrés d'arc.

 ➔   Les notations pour les degrés (°) et celles des subdivisions en minutes (') et secondes (") remontent à Peletier du Mans (1549). Rappel : 1° = 60', 1' = 60'', soit 1° = 3600''. Au tout début du 19è siècle apparaît une nouvelle unité de mesure : le grade, 100 grades équivalant à 90°, mesure de l'angle droit.

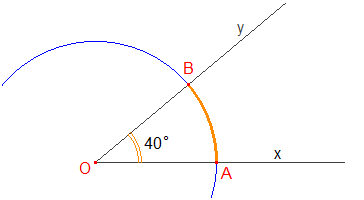
Angles, arcs et mesure en degrés et grades (approche élémentaire) : »

Mécanique céleste :

Par ses observations astronomiques (mouvements apparents de la Lune et du Soleil principalement) et avec l'aide des instruments qu'il conçut, comme l'astrolabe (» ci-dessous), Hipparque comprend que les modèles d'orbites circulaires concentriques d'Eudoxe et de Conon de Samos ne sont pas satisfaisants, les planètes observées ne restant manifestement pas à la même distance de la Terre lors de leurs révolutions.

                » Aristarque , Ptolémée , Copernic , Kepler

∗∗∗ Angles et mesures (exercices niveau collège)

On doit à Hipparque des notions, résultats, découvertes et inventions remarquables. En particulier :


L'astrolabe d'Hipparque selon Ptolémée - Illustration et description du fonctionnement
Source : Histoire de l'astronomie depuis ses origines jusqu'à nos jours, par Ferdinand Hoefer (1873), » description & réf.7

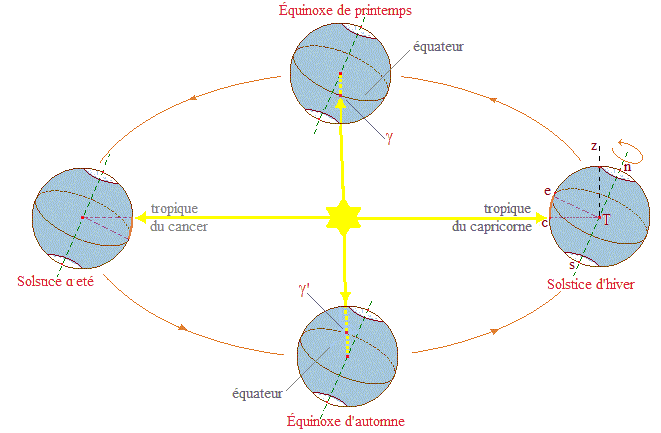
Schéma héliocentrique expliquant le phénomène des saisons
 i  tropique provient du grec tropikos formé sur tropein = tourner et  tropê = tour, révolution. Avant Copernic, le système solaire était
considéré comme géocentrique (la Terre tourne autour du Soleil), ce qui ne change pas l'interprétation.

Équinoxes : issue du latin (aequus = égalité, nox = nuit) pour signifier l'égalité de durée du jour et de la nuit, événement se produisant en mars (équinoxe de printemps, 20/21 mars) et en septembre (équinoxe d'automne, 21/22 septembre), époque de l'année où le Soleil semble traverser le plan de l'équateur aux points γ (point vernal) et γ'. En ces dates, le soleil se lève exactement à l'Est et se couche exactement à l'Ouest. De plus, cet alignement équatorial provoque des marées plus conséquentes (marées d'équinoxe).

Solstices : du latin solstitium formé sur sol = soleil et status = arrêt, état de repos, pour signifier que le soleil atteint, par rapport à l'écliptique, son point le plus bas le 21/ou 22 décembre (début de l'hiver dans l'hémisphère nord et de l'été dans l'hémisphère sud) ou le plus haut le 21/ou 22 juin (début de l'été dans l'hémisphère nord et de l'hiver dans l'hémisphère sud). Mathématiquement, la déclinaison du soleil passe par un extremum et, par suite, semble stationnaire pendant 3 ou 4 jours.

♦ Au solstice d'hiver, le rayonnement est maximal dans l'hémisphère sud : les rayons du Soleil "frappent" perpendiculairement le tropique du Capricorne, parallèle de latitude -23° 27' = ^eTc = ^zTn, inclinaison de l'axe de rotation de la Terre par rapport à l'écliptique. La calotte polaire boréale nord, Groenland) ne voit pas le Soleil se lever, l'hémisphère nord reçoit obliquement le rayonnement solaire. La calotte polaire sud reste au Soleil toute la journée.

♦ Au solstice d'été, au contraire, le rayonnement est maximal dans l'hémisphère nord : les rayons du Soleil "frappent" perpendiculairement le tropique du Cancer, parallèle de latitude +23° 27'. La calotte polaire sud ne voit pas le Soleil se lever et celle du nord reste au Soleil toute la journée (soleil de minuit).

Formule de la magnitude en fonction de l'éclat : »

Sphère céleste, point vernal : »           Zodiaque et carte du ciel : »        » Nasir-ad-din at-Tusi

La machine d'Anticythère :    

Certains spécialistes attribuent à Hipparque la machine d'Anticythère, un appareil astronomique à engrenages (une trentaine, en bronze) d'une complexité stupéfiante pour l'époque, susceptible de déterminer la position des astres, basée sur les 365 jours du calendrier égyptien et le cycle de Méton. Son nom provient de l'île grecque Anticythère au sud-est du Péloponnèse où la machine fut trouvée dans une épave d'une galère romaine (découverte en 1900) et récupérée par l'équipe du commandant Cousteau (célèbre océanographe français, 1910-1997) en 1976. D'autres l'attribuent à Archimède mais les connaissances trigonométriques liées à son usage penchent en faveur d'Hipparque. Quoi qu'il en soit, on en trouvera une description précise sur Wikipedia :

Machine d'Anticythère (lien externe) : »

La théorie des épicycles :     

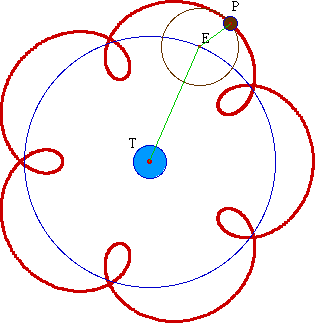
Se basant sur une idée d'Apollonius de Perge, il invente un système savant rendant mieux compte des trajectoires observées dans le cadre d'un système géocentrique (les planètes tournent autour de la Terre) : ci-dessous la planète P décrit uniformément un cercle, dit épicycle, autour d'un point théorique E, ce dernier tournant uniformément autour de la Terre T. Pour un observateur lié à T, la trajectoire résultante est généralement une épicycloïde dont la forme dépend des vitesses angulaires de E et P (une telle courbe peut être une ellipse).

L'hypothèse excentrique :    

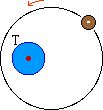
Une hypothèse plus simple, également mentionnée par Hipparque, fut l'excentrique : la planète P décrit un cercle non centré en T, dit cercle déférent (ci-dessous) expliquant alors les phénomènes observés d'apogée (point le plus éloigné de la Terre) et de périgée (point le plus proche de la Terre) pressenties par la diminution et l'augmentation périodiques de l'éclat des planètes au cours de l'année.

 i  Apogée est issu du préfixe grec apo indiquant l'éloignement et de gê = terre (comme dans géométrie = mesure de la terre). Périgée provient de perigeios construit sur gê  et peri = autour : autour de la Terre, au sens de non loin de la Terre.

On remarque que l'hypothèse excentrique s'approche d'une solution elliptique. Cependant, deux siècles et demi plus tard, Ptolémée reprendra les deux modèles géocentriques d'Hipparque dans sa théorie, plus complexe, des équants. Ce n'est qu'au début du 17è siècle, suite aux travaux de Copernic et de Galilée, que Johannes Kepler résoudra définitivement le problème selon un modèle héliocentrique (du grec helios = soleil) : les planètes tournent autour du Soleil et leurs orbites sont des ellipses dont un des foyers est le Soleil.


•••  Épicycles selon Hipparque & animation : »
 

La projection stéréographique :

Concernant la représentation de la Terre, il conçut la notion de projection stéréographique : à tout point M de la demi-sphère Σ autre que le pôle O, on associe le point M' intersection de son plan équatorial et de la demi-droite [OM).

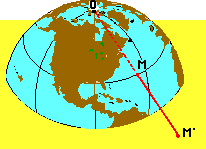
Dans le cas considéré (demi-sphère), les points de Σ se projettent à l'extérieur du cercle équatorial. Dans le cas d'une sphère "posée" sur son pôle sud S, l'image serait son plan tangent en S.

Mathématiquement, si nous appelons (P) le plan équatorial de Σ, nous sommes en présence d'une inversion géométrique de pôle O, de rapport 2r2, r désignant le rayon de la sphère. Le cercle équatorial est invariant.

 ➔  Ce résultat peut s'obtenir par des considérations trigonométriques élémentaires :

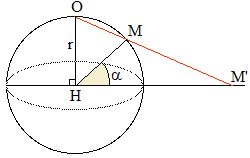
Dans le triangle OHM, on a selon Al-Kashi : OM2 = 2r2 - 2r2cos(π/2 - α) = 2r2(1 - sinα). Un calcul élémentaire des angles du triangle OHM conduit à ^OM'H = π/4 - α/2, d'où OM' = r/sin(π/4 - α/2). Or, 2sin2(π/4 - α/2) = 1 - cos(π/2 - α) = 1 - sinα et finalement : OM2 × OM'2 = 4r4, soit : OM × OM' = 2r2.

L'usage de la puissance d'un point par rapport à un cercle conduit très simplement au résultat, eu égard à OM'2 = R2 + HM'2 car la puissance de M' par rapport au cercle est d'une part M'M x M'O et d'autre part : M'H2 - r2.

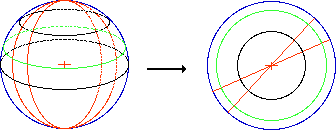
Par cette inversion la sphère est transformée en (P). Les cercles passant par le pôle (les méridiens) sont transformés en droites et les cercles parallèles à (P), les parallèles, sont transformés en cercles. Sachant que l'inversion conserve les angles : pour cette raison, la projection stéréographique est dite conforme.

           

Projection stéréographique et sphère de Riemann : »

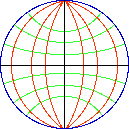
 ➔  Si nous voulons obtenir une carte de l'hémisphère nord, on choisit le pôle sud S comme pôle d'inversion. Tous les points de l'hémisphère nord seront projetés à l'intérieur du cercle équatorial, ce qui fournit, en se limitant à quelques-uns de ces cercles, une projection comme ci-dessus à gauche.

Il y aura moins "d'écrasement" pour les parties les plus au nord. En cartographie, on utilise plutôt un des points O de l'équateur comme pôle d'inversion : projection stéréographique équatoriale. Le plan de projection passe alors par les pôles Nord et Sud et on pourra représenter l'hémisphère ne contenant pas O. Dans ce cas, méridiens et parallèles sont transformés en (arcs de) cercles (à droite).

Projection Lambert : »            Projection conforme de Mercator : »          » Johann Werner
 

Source : Histoire de l'astronomie depuis ses origines jusqu'à nos jours, par Ferdinand Hoefer (1811-1878), pages 167 et suivantes :








 

 ➔  Pour en savoir plus :

  1. The history of tropical year, par Jean Meus & Denis Savoie (British Astronomical Association) :
    https://articles.adsabs.harvard.edu/pdf/1992JBAA..102...40M

  2. Solstices, équinoxes et précession, vidéos YouTube :
    a) https://www.youtube.com/watch?v=yARKHaPmE0o (Bright Blue)
    b) https://www.youtube.com/watch?v=XY6XWt2HRLA (theRealDysko)

  3. Pourquoi y a-t-il des saisons ?, vidéo YouTube : https://www.youtube.com/watch?v=Ps1UPv4ETRk

  4. Précession des équinoxes :
    a) http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/divers/equinoxe.html
    b) Hipparque et la précession des équinoxes :
    http://www.afhalifax.ca/magazine/wp-content/sciences/AMA2009/hipparque/Untitled.htm

  5. Magnitude d'une étoile :
    a) Centre de recherche astrophysique de Lyon (CRAL) :
    https://cral-perso.univ-lyon1.fr/labo/fc/cdroms/stages14-15/distances/ST_doc/magnitudes.pdf
    b) Magnitude apparente et absolue, une vidéo YouTube de Julien Astruc : https://www.youtube.com/watch?v=Llx377-cALE
        Stellar Brightness and Pogson's Magnitudes, vidéo Youtube de Jason Kendall (» William Paterson Univ.) :
        https://www.youtube.com/watch?v=PcRLQ_QYbfM
    c) Magnitude apparente, page Wikipédia : https://fr.wikipedia.org/wiki/Magnitude_apparente
       Magnitude absolue et module de distance, page Wikipédia : https://fr.wikipedia.org/wiki/Module_de_distance
    d) To measure the sky : https://books.google.fr/books?id=34owDQAAQBAJ&pg=PA22#v=onepage&q&f=false
        Cambridge university press, en lecture partielle sur Google livres.
    e) Discussion sur la magnitude de Véga dont la magnitude apparente est 0 par convention sur webastro.net
    f) Qu'est-ce qu'un lumen ? : http://www.blog-couleur.com/?Qu-est-ce-qu-un-lumen

  6. a) Les armilles sur Wikipédia : https://fr.wikipedia.org/wiki/Armille_(astronomie)
    b) Les quadrants sur Wikipédia : https://fr.wikipedia.org/wiki/Quadrant_(instrument)

  7. c) L'astrolabe sur Wikipédia : https://fr.wikipedia.org/wiki/Astrolabe

  8. Histoire de l'astronomie depuis ses origines jusqu'à nos jours, par Ferdinand Hoefer (1811-1878) :
    https://books.google.fr/books?id=X79KAAAAMAAJ (Hipparque : page 159 et suivantes de la pagination)

  9. Histoire de l'astronomie moderne depuis l'École d'Alexandrie, par Jean Sylvain Bailly (1779) :
    https://books.google.fr/books?id=v8RZAAAAcAAJ&pg=PA242

Dioclès  Vitruve
© Serge Mehl - www.chronomath.com