ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BRAHMAGUPTA
(ou Brahamagupta)
, indien, vers 598-668 |
Ce mathématicien et astronome indien vécut à Ujjain, une des sept villes sacrées de l'Inde dans le bassin du Gange. Ujjain fut le berceau des astronomes indiens. Ci-dessous, à droite, l'ancien observatoire Vedh Shala, bâti par le maharadja de Jaipur en 1719 et où il fut décidé le passage du méridien d'origine des géographes indiens : en quelque sorte le "Greenwich indien".
Dans le cadre de ses calculs astronomiques, Brahmagupta s'intéressa à l'algèbre et aux équations diophantiennes, complétant des travaux d'Aryabhata. Il affirme la sphéricité de la Terre et sa rotation sur elle même. Son manuscrit, le Brāhmasphuṭasiddhānta, écrit vers 628, conservé à la British Library de Londres, ne nous fut connu qu'au début du 19è siècle grâce à la traduction qu'en fit le magistrat et botaniste Henri Thomas Colebrooke (1765-1837), admirateur de la civilisation indienne.
Par indien ou indienne, il faut
entendre un habitant ou un concept relatif à l'Inde. La vraie ! Pas celle que
Christophe Colomb croyait avoir découverte en 1492 en débarquant aux Bahamas, se
croyant en Asie... Ceci dit, on peut souvent parler de la
science hindoue car,
généralement, les scientifiques de l'Inde ancienne furent des religieux adeptes
de l'hindouisme et de ses trois dieux, la Trinité hindoue : Brahma (le
créateur), Vishnu (le préservateur de l'Univers) et Shiva (ou
çiva, le destructeur, mais
aussi fécondateur, détruisant pour créer).
Brahmagupta emploie dans ses calculs un système décimal dont le graphisme est très proche de nos chiffres actuels dits arabes, fruit d'une évolution commençant au 3ème siècle avant J.-C. et introduit le zéro (notation o), clé de voûte de ce système, que les Arabes adopteront timidement dès le 9è siècle avec Al-Khwarizmi puis Al-Biruni à la fin du 10è siècle, en remplacement du système sexagésimal.
Le célèbre "chiffre" manqua cruellement aux grandes civilisations babyloniennes, égyptiennes et grecques. Son apparition en Inde, tout particulièrement dans l'œuvre de Brahmagupta, est un pas de géant en algèbre. En Inde, d'une province à l'autre, les notations différaient et évoluèrent sur plusieurs siècles :
Brahmagupta est sans doute le premier à user des nombres négatifs dans des calculs commerciaux afin de signifier les pertes et à les utiliser en algèbre en énonçant la règle des signes relative à la multiplication.
Mais c'est quoi 0 ? comment le définir ?
La définition la plus simple est sans doute exprimée par : zéro est l'entier obtenu en soustrayant un nombre entier à lui-même.
De manière contemporaine, dans l'ensemble N* = {1, 2, 3, ...} des entiers naturels au moins égaux à 1, considérons le nombre 7; il a un successeur (8, c'est à dire 7 augmenté de 1) et un prédécesseur (6, c'est à dire 7 diminué de 1). Un successeur ou prédécesseur, lorsqu'il existe, est unique. On peut alors définir 0 en tant qu'entier naturel dont le successeur est 1. Le prédécesseur de 1 est alors 0 et on a 0 + 1 = 1.
∗∗∗
En conférant à 0 le statut d'entier à part entière dont l'addition est associative et commutative, montrer que
0 + 0 = 0 et, par récurrence, 0 + n = n + 0 pour tout entier n : 0 est l'élément neutre de l'addition.
0 peut être défini au moyen d'une propriété pythagoricienne selon laquelle tout entier au moins égal à 2 est moyenne arithmétique des entiers qui l'entourent. Si l'on veut que 1 possède cette propriété, il nous faut inventer 0. Cette introduction du zéro est abordée sur la page consacrée à l'Islam et la numération décimale.
Brahmagupta précise verbalement les règles de calculs avec le zéro (pas encore de symbolisme). En notation actuelle, a, b, c, ... désignent ci-dessous des profits (nombres positifs) et -a, -b, -c des pertes (nombres négatifs) :
La somme de deux zéros est zéro :
0 + 0 = 0.
Augmenté ou diminué de zéro perte ou
profit reste inchangé(e) :
a ± 0 = a et -a ± 0 = -a.
Si un bien égale une dette (même
montant), leur somme est zéro :
a + (-a) = 0.
La somme de deux profits a et b est un profit;
celle de deux pertes est une perte :
si s = a + b somme de deux profits, alors (-a) + (-b) = -s.
La somme d'un profit et d'une perte est leur
différence :
a + (-b) = a - b
Dans une différence, le plus petit
(montant) se retranche du plus grand mais si l'on soustrait le plus grand du
plus petit, la différence est changée (perte ↔ profit) : si b > a,
alors a - b = -(b - a);
• par exemple 3 - 7 = - (7 - 3) = -4.
Arithmétique et le zéro selon Raymond Queneau (INA) : »
➔ Inconnue jusqu'au 16è siècle, la civilisation Maya, découverte par les espagnols au sud de l'actuel Mexique, usait d'un système de numération positionnel de base 20 présentant un symbole spécifique pour désigner l'absence d'une puissance de 20 dans la décomposition d'un nombre et que l'on peut interpréter comme un "zéro".
Systèmes de numération : » Le système maya : »
YouTube Les origines du zéro, de Babylone à
Fibonacci
| Résolution d'équations diophantiennes : |
Brahmagupta précise certaines relations métriques dans le triangles rectangle, en particulier :
En 628, dans son Brâhma-Sphutasiddhânta, Brahmagupta revient sur les équations indéterminées en nombres entiers de la forme ax + by = c étudiées par Diophante et Aryabhata, en donnant non pas des solutions particulières comme ses prédécesseurs mais l'ensemble des solutions.
Il résout, sur des cas particuliers inspirés par
Héron d'Alexandrie relatifs à la détermination de
triangles à aire entière et côtés entiers consécutifs, de difficiles
équations comme :
dont (2,1), (7,4), (26,15), ... sont des solutions (» page Héron & réf.2). Brahamgupta calcula également une solution équation de l'équation x2 - 92y2 = 1 dont la solution (x,y) = (1151,120) est minimale en x (» réf.3).
Au 12è siècle, Bhaskara traitera ce type d'équations dans un cadre plus général. De nos jours, on parle d'équations de Pell ou de Pell-Fermat, de la forme :
Par ailleurs, le concept de congruence, cher à Gauss, apparaît chez Brahmagupta dans son Bhrama-Sphuta-Siddhanta, traité d'astronomie et de mathématiques, à travers la résolution, sur des cas particuliers, de systèmes de la forme :
Les congruences arithmétiques sont nées de l'astronomie de par les observations de phénomènes se répétant périodiquement. Elles se retrouvent également précocement, pour les mêmes raisons, dans les mathématiques chinoises où l'on rencontre souvent le module k = 60 (correspondant à deux lunaisons).
Dans son livre, Victor J. Katz cite un cas traité par Brahmagupta :
n ≡ 10 [137] et n ≡ 0 [60]
Ce système peut être résolu facilement en constatant qu'elle revient à écrire n = 60x et n - 10 = 137y. On en déduit : 60x - 137y = 10, équation que l'on résout par la méthode de Bézout.
| Une belle formule pour l'aire d'un quadrilatère inscriptible |
Brahamagupta
établit la formule de l'aire d'un
quadrilatère convexe inscriptible,
c'est à dire dont les sommets sont sur un même cercle, en fonction de la mesure de ses côtés :
Si a, b, c et d désignent la mesure des côtés et p = (a + b + c + d)/2 le demi-périmètre, on a :
Cette formule généralise au quadrilatère inscriptible celle de l'aire du triangle (toujours inscriptible...) souvent attribuée au mathématicien grec de l'antiquité Héron d'Alexandrie.
Il précise également que les diagonales [AC] et [BD] ont pour mesures respectives :
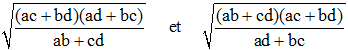
Leur produit est AC.BD = ac + bd.
➔ Pour en savoir plus :
Al-Khwarizmi