
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


Né à Pise, Galileo Galilei y fit ses premières études. Ses parents s'installent à Florence et il est voué, par la volonté de son père (compositeur et professeur de musique), à des études de théologie qu'il abandonne contre son gré au profit d'études de médecine à Pise.
Mais, dès 1583, Galilée s'intéresse finalement plus à l'astronomie, les sciences physiques et les mathématiques et, de retour à Florence, il consolide ses études tout en commençant à enseigner. Parmi ses élèves figurent Viviani et Torricelli.
Finalement professeur de mathématiques à Pise (1589) puis à Padoue (Padova) quatre ans plus tard, Galilée émet dès lors des critiques à l'encontre de la physique d'Aristote et soutient les théories d'Archimède sur la gravitation et, discrètement, car risqué..., celle de Copernic sur le système du Monde (il enseignait alors sans y croire, la théorie de Ptolémée).
Grâce à sa célèbre lunette astronomique, inventée en 1609, il découvrit les 4 premiers satellites de Jupiter, dites Lunes galiléennes, à savoir : Callisto, Europe, Io et Ganymède.
➔ Selon Descartes, la première lunette astronomique aurait été construite en Hollande, avant Galilée, par l'astronome Adrien Metius. On attribue souvent à Galilée l'invention du thermomètre (1592) mais il apparaît, là encore, une paternité antérieure : Philon de Byzance, ingénieur grec ayant vécu au 3è siècle avant J.-C., en avait construit un dont le principe était basé sur la surpression de l'air dans un tube fermé. Ce même principe fut d'ailleurs repris par Héron d'Alexandrie.
| Le fondateur d'une branche fondamentale de la physique, la dynamique : |
Physicien, astronome, ingénieur talentueux, Galilée énonce les lois de la pesanteur en étudiant la chute des corps sur un plan incliné, énonça le principe de la résultante des forces appliquées à un point ou à un solide, découvrit les lois régissant le pendule. Il créa ainsi la Dynamique (du grec dunamis = force) : branche de la mécanique étudiant les relations entre les forces qui régissent les mouvements.
Repère (ou référentiel) galiléen :
En hommage à ce grand savant, le qualificatif de galiléen fut attribué en mécanique à un repère (O,x,y,z,t) de l'espace dans lequel s'applique, pour un système matériel S la relation fondamentale de la dynamique (seconde loi de Newton)
F = m × dvG/dt
où m désigne la masse du système, vG le vecteur vitesse de son centre de gravité G (les physiciens disent aussi centre d'inertie ou centre de masse) et F la résultante des forces s'appliquant à S. S'agissant d'un point matériel, le système S se confond avec G et on peut écrire alors F = m × γ, où est le vecteur accélération γ de G, dérivée du vecteur vitesse.
» Concernant les observations astronomiques, le référentiel géocentrique (pour signifier que son origine est le centre de notre planète) dont les trois axes pointent vers des étoiles fixes de notre galaxie peut être considéré comme galiléen. L'idée de se repérer à l'aide d'étoiles très éloignées considérées comme fixes remonte à Aristote et sa sphère des étoiles, confortée par Hipparque et Ptolémée. Aujourd'hui, on sait qu'elles sont en fait en mouvement, dû en particulier à l'expansion observée de l'univers, mais effectivement négligeable le temps d'une observation (moins de 1 minute d'arc par an).
Dans un repère galiléen, si vG est constante (quantité de mouvement q = m × vG) alors la résultante F des forces est nulle : le système S est au repos (vG = 0), ou bien son centre de gravité est en mouvement de translation rectiligne uniforme relativement à ce repère (le système peut gesticuler, ce qui importe là est le comportement de G...) et cette propriété également appelé principe d'inertie, caractérise les repères galiléens.
Métrique de l'espace temps, repères non galiléens, transformation de Lorentz : »
 Galilée
découvrit la trajectoire
parabolique
des projectiles et la loi de la chute des corps dans l'espace : mouvement
uniformément accéléré, en constatant que le rapport des distances (y) parcourues
égale le rapport des carrés des temps (x), d'où une relation de la forme y = kx2.
Galilée
découvrit la trajectoire
parabolique
des projectiles et la loi de la chute des corps dans l'espace : mouvement
uniformément accéléré, en constatant que le rapport des distances (y) parcourues
égale le rapport des carrés des temps (x), d'où une relation de la forme y = kx2.
Et c'est du haut de la célèbre tour penchée (ça tombe bien...) de sa ville natale que Galilée laissa, paraît-il, tomber deux boules d'acier de poids distincts afin d'envisager le principe d'indépendance des masses dans la chute libre (chute sans vitesses initiale) des corps dans le vide. Ce n'était pas le cas en l'occurrence, mais par temps calme et en utilisant des boules suffisamment lourdes, on peut estimer que la résistance de l'air est négligeable.
A droite la tour penchée de Pise, source Wikipedia : https://fr.wikipedia.org/wiki/Tour_de_Pise →
➔ à propos de la chute libre des corps et de la rotation de la Terre autour de son axe, le chimiste et physicien allemand Ferdinand Reich (1799-1882) a pu mettre en évidence (1833) la rotation de la Terre en prouvant qu'un corps massif tombant en chute libre subit une déviation vers l'est du fait de la rotation de la Terre d'ouest en est. On pourra à ce sujet consulter le lien in fine (» réf.5).
| Galilée et la rotation de la Terre sur elle-même, E pur, si muove... : |
 Après
de multiples hésitations dues à des dénonciations auprès du Saint-Siège
n'annonçant rien de bon dès 1610, car lui interdisant alors de diffuser ses
idées "absurdes et hérétiques", Galilée confirma, en 1632, dans son mémoire
Dialoghi quatro, sopra i due massimi sistemi del mundo, Ptolomaïco et
Copernico (Quatre dialogues sur les principaux systèmes du Monde,
à savoir ceux de Ptolémée et Copernic), la théorie
héliocentrique de Copernic
selon laquelle le Soleil est au "centre" du système planétaire, et non la Terre
comme le soutenait Aristote : la Terre, tout en tournant sur elle-même, tourne autour du
Soleil.
Après
de multiples hésitations dues à des dénonciations auprès du Saint-Siège
n'annonçant rien de bon dès 1610, car lui interdisant alors de diffuser ses
idées "absurdes et hérétiques", Galilée confirma, en 1632, dans son mémoire
Dialoghi quatro, sopra i due massimi sistemi del mundo, Ptolomaïco et
Copernico (Quatre dialogues sur les principaux systèmes du Monde,
à savoir ceux de Ptolémée et Copernic), la théorie
héliocentrique de Copernic
selon laquelle le Soleil est au "centre" du système planétaire, et non la Terre
comme le soutenait Aristote : la Terre, tout en tournant sur elle-même, tourne autour du
Soleil.
Une théorie allant à contre courant des idées régnant au sein des pensées obscurantistes de l'époque, attachées aux doctrines antiques de la Bible. L'œuvre fut immédiatement soumise aux doctes jurés de l'inquisition et déclarées hérétiques par le pape Paul V en 1633. Galilée sera condamné et devra abjurer tout en énonçant tout bas, selon la légende, cette phrase célèbre :
Pourtant, à l'époque de Copernic, le pape Paul III avait agréé, certes à contrecœur, les idées coperniciennes. De par la volonté du pape Benoît XIV, ce n'est qu'en 1759 que Galilée et Copernic seront retirés de l'Index. La réhabilitation officielle de Galilée par l'Église est due à Jean-Paul II, élu pape en 1978.

Photo (perso) du ciel prise en pose au voisinage
de l'étoile polaire, étoile
α
de la Petite Ourse,
alias Polaris, proche du pôle nord céleste. Si ce n'est la Terre, c'est le ciel qui tourne...
 En
1851, Léon Foucault
physicien, ingénieur et astronome (1819-1868),
installa sous la coupole du Panthéon (Paris) le pendule portant son nom qui lui
permit également de prouver la rotation de la Terre autour de son axe :
En
1851, Léon Foucault
physicien, ingénieur et astronome (1819-1868),
installa sous la coupole du Panthéon (Paris) le pendule portant son nom qui lui
permit également de prouver la rotation de la Terre autour de son axe :
Un pendule pesant oscille dans un plan vertical fixe (p) passant par son point d'attache A. Un stylet situé sous la sphère laissait une trace dans du sable étalé à la base, ce qui permit de constater que tout se passait comme si le plan (p) du pendule tournait autour de A. (p) étant invariant, ce ne pouvait être que la Terre qui tournait. On pourra à ce sujet consulter les liens in fine (» réf.6 & 7). à noter qu'après la fin des travaux sous la coupole, le pendule y a repris sa place.
Deux petites erreurs mathématiques... :
♦ Galilée s'intéressa au problème brachistochrone : recherche du support (trajectoire) permettant la descente la plus rapide d'un point roulant (un toboggan en quelque sorte). Il crut prouver que la solution était un arc de cercle. La "preuve" de Galilée est en ligne (fichier pdf en italien, » réf.8).
♦ Galilée pensa de même à tort que la chaînette était une parabole. La chaînette est la courbe que l'on peut admirer en tenant un collier ou une chaîne par ses extrémités ou en observant, de nos jours, les câbles électriques à haute tension suspendus entre deux puissants pylônes.
 Il
fallut attendre la fin du 17e siècle et une certaine
maturité du calcul différentiel (dont on attribue la
paternité à Leibniz
et à Newton),
avec Jakob
Bernoulli, pour connaître la
véritable nature de ces courbes :
Il
fallut attendre la fin du 17e siècle et une certaine
maturité du calcul différentiel (dont on attribue la
paternité à Leibniz
et à Newton),
avec Jakob
Bernoulli, pour connaître la
véritable nature de ces courbes :
Il montrra que la solution brachistochrone est un arc de cycloïde (on lui doit cette appellation) et que la chaînette est apparentée à la fonction cosinus hyperbolique, notée ch ou, plus souvent, aujourd'hui cosh :
➔ Un lien intéressant cependant entre chaînette et parabole : le foyer d'une parabole qui "roule" sans glisser sur une droite décrit une chaînette.
 |
Les paradoxes de l'infini : |
Galilée fut aussi le premier à remettre en cause un des axiomes d'Euclide affirmant que le tout est plus grand que la partie : afin d'expliquer les paradoxes inhérents aux ensembles infinis, il constate aussi qu'il y a "autant" de points dans un petit et un grand segment comme le confirme la figure ci-dessous générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
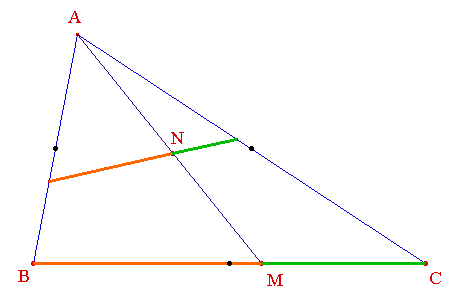

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer M ainsi que les sommets A, B et C du triangle. Vous constatez
qu'à chaque
point M du "grand" segment correspond un point N
du petit et inversement.
Les points noirs indiquent les milieux des
côtés. Ne pas croire naïvement
que le segment qui joint les milieux de deux côtés
contient deux fois moins de points que le côté opposé...
Plus mathématiquement, considérer l'application f qui à M associe N : c'est une bijection du "petit" segment sur le "grand" (homothétie de centre A) .
Galilée présente également en exemple paradoxal qu'il y a "autant" d'entiers naturels que de carrés de ces entiers, comme le montre la correspondance (bijection, en termes modernes) :
D'où l'idée que de parler d'un ensemble infini dans sa globalité (infini actuel) n'a pas de sens. La mathématique grecque traita de l'infini potentiel : collection d'objets abstraits ou concrets qui, s'ils sont rangés, contiendra toujours un objet au-delà (ou sinon en deçà) de l'un quelconque d'entre eux.
Il fallut attendre Dirichlet, Dedekind et Cantor pour une définition précise d'un ensemble infini et une distinction claire entre l'infini dénombrable et le continu.
Cantor et les notions de cardinal et d'équipotence : »

➔ Pour en savoir plus :