
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Ce sont les Pythagoriciens (Pythagore, Nicomaque,...) puis Euclide qui se sont tout particulièrement intéressés aux nombres entiers et aux problèmes de divisibilité. Mais le système décimal n'était pas encore en place !
Si a et b sont deux entiers naturels, b n'étant pas nul, on dit que b divise a ou que b est un diviseur de a ou que b est un facteur de a ou que a est un multiple de b s'il existe un entier q tel que a = b × q.
➔ Autrement dit, b est un diviseur de a si, dans la division euclidienne de a par b, le reste est nul.
8 est un diviseur de 24 car 24 = 8 × 3; 8 est un des deux facteurs du produit 8 × 3.
Un diviseur d'un nombre autre que 1 et lui-même est dit propre.
Théorème :
Soit p un entier non nul.
Conséquences :
♦ Divisibilité par 2 : un entier est divisible par 2 s'il se termine par 0, 2, 4, 6 ou 8. En effet tout entier n s'écrit 10k + u, u étant le chiffre de ses unités; 2 divise 10k donc 2 doit diviser u, cette condition est clairement nécessaire et suffisante.
♦ Divisibilité par 5 : un entier est divisible par 5 s'il se termine par 0 ou 5. Evident en écrivant là encore n = 10k + u
♦ Divisibilité par 4 :
un entier est divisible par 4 si le nombre formé avec ses deux derniers chiffres
est divisible par 4.
En effet tout entier n s'écrit 100k + (10u + v), u
étant ici le chiffre des dizaines et v celui des unités ses unités; 4 divise
100k donc 4 doit diviser 10u+v, cette condition est clairement nécessaire et
suffisante.
Exemples : 72 est divisible par 4 (k = 0); 752 est divisible par 4 : 652 = 700 +
52 (k = 7, u = 5, v = 2) et 52 = 4 × 13.
♦ Divisibilité par 25 : un entier est divisible par 25 si le nombre formé avec ses deux derniers chiffres est multiple de 25, donc s'il se termine par 00, 25, 50 ou 75. En effet tout entier n s'écrit 100k + (10u + v), u étant ici le chiffre des dizaines et v celui des unités ses unités; 25 divise 100k donc 25 doit diviser 10u+v, cette condition est clairement nécessaire et suffisante.
♦ Divisibilité par 3 ou par 9 : un entier est divisible par 3 (resp. 9) si la somme de ses chiffres est divisible par 3 (resp. 9). En effet, il est clair que toute puissance de 10 diminué de 1 est divisible par 9 et donc aussi par 3 : 10n - 1 = 99....9 (nombre constitué de n neuf). Or entier n s'écrit (» numération décimale) : a × 10n + b × 10n-1 + a × 10n-2 + ... + 10k + u = a × (10n - 1) + b × (10n-1 - 1) + c × (10n-2 - 1) + ... + 10k + (a + b + c + ... + k + u) : n sera divisible par 3 ou 9 si et seulement si a + b + c + ... + k + u l'est aussi.
Pour les puristes : Si le "il est clair" vous paraît détourner la difficulté, soyons plus précis : on sait que (an - bn) = (a - b)(an-1 + an-2b + an-3b2 + ... + an-2b + bn-1); or 10n - 1 = 10n - 1n = (10 - 1)(10n-1 + 10n-2 + ... + 10 + 1) = 9 × (10n-1 + 10n-2 + ... + 10 + 1); on remarque que la ( ) s'écrit 111...1, ce qui est bien conforme à notre attente... on peut, plus subtilement, mais plus simplement..., utiliser les congruences : 10 ≡ 1 [9], donc 10n ≡ 1n [9], donc 10n - 1 ≡ 0 [9].
Preuve par 9 : »
♦ Divisibilité par 11 :
Un entier n est divisible par 11 si
la somme alternée de ses chiffres à partir de la droite (chiffre des unités) est divisible par 11
(par alternée, on entend ajouter/soustraire alternativement).
Preuve : on peut prouver ce résultat facilement par les
congruences
en notant que 102p ≡
1 [11] alors que 102p+1
≡
-1 [11] ou de façon élémentaire en écrivant comme pour la
divisibilité par 9, n = a
× 10n + b
× 10n-1 + c
× 10n-2
+ ... + 10k + u.
Écrivons alors l'entier n en commençant par les unités : n = u + 10k + 100m + c × 10n-2 + b × 10n-1 + a × 10n + ... . Vu les considérations ci-dessus, ce nombre est de la forme 11p + [u - k + m - ... + (-1)n × a] et sera divisible par n à condition que le crochet le soit. Ce qu'il fallait démontrer.
82456 est divisible par 11 car 6 - 5 + 4 - 2 + 8 = 11, on a 82456 = 11 × 7496. 193919 est divisible par 11 car 9 - 1 + 9 - 3 + 9 - 1 =22
Preuve par 11 : »
|
Nombre de diviseurs d'un entier naturel, somme des diviseurs : |
Soit n = p1α ×
p2β × ...
× pkγ
la décomposition en facteurs premiers d'un
entier n non premier.
Son nombre de diviseurs ( y compris 1 et lui même) est le produit : (α+1) ×(β+1) ×... ×
(γ+1).
i Ce nombre de diviseurs est parfois noté τ(n) : on parle ainsi fonction tau, appellation provenant possiblement de l'allemand Teiler = diviseur (teilen = diviser) sachant que les allemands utilisent également dividieren (diviser) et divisor.
Par exemple : 24 = 23 × 3, donc τ(n) = (3 + 1) × (1 + 1) = 8.
Justifions la formule sur cet exemple : la décomposition de tout diviseur de 24 contiendra ou non le facteur 2 et le facteur 3. Il y a 4 façons d'utiliser le facteur 2 (0 fois à 3 fois) et 2 façons d'utiliser le facteur 3 (0 ou 1 fois). Il y a donc 4 × 2 = 8 façons de "fabriquer" un diviseur de 24.
➔ Connaissant le nombre de diviseurs, on obtiendra facilement l'ensemble des diviseurs par épuisement des cas.
Concernant 24 = 23 × 3 : en n'utilisant que des puissances de 2, on obtient 1 = 2o , 2 , 4 , 8 = 23, que des puissances de 3 : on n'obtient que 1 et 3, puis par combinaison : 1 , 2 , 4 , 8 , 3 , 6 , 12 , 24 : 8 cas.
Concernant 120 = 23 × 3 × 5 : il nous faut trouver 16 diviseurs. On a déjà les 8 diviseurs de 23 × 3 = 24, auxquels s'ajoutent tous les produits par 5, soit, après remise en ordre croissant : 1, 2 , 3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 20 , 24 , 30 , 40 , 60 , 120.
***
1. Décomposer N = 2940 et D = 5145 en produit de facteurs
premiers, simplifier la fraction F = 2940 / 5145.
Rép. :
N = 22 ×3 × 5 ×72
, D = 3 × 5 ×73, F = 4/7.
2. Établir la liste de tous les diviseurs de 5145.
Rép. : 5145 possède 2 × 2 × 4 = 16 diviseurs. Liste :
On commence à 1 et on écrit ensuite en 1ère ligne les diviseurs par ordre
croissant. En seconde ligne, on écrit
les quotients de 5145 par ces diviseurs qui sont eux-mêmes des diviseurs. Dès
qu'il y a redondance, le tableau est terminé.
Par exemple ci-dessous, on ne traite pas le cas 343 = 73 qui
fournirait 15 déjà obtenu. On a bien nos 16 diviseurs.
| 1 | 3 | 5 | 7 | 15 | 21 | 35 | 49 |
| 5145 | 1715 | 1029 | 735 | 343 | 245 | 147 | 105 |
Radical d'un nombre : »
Somme des diviseurs d'un entier naturel :
On note σ(n) la somme des diviseurs d'un entier naturel n. Considérons n = pα un entier naturel, puissance α-ème d'un nombre premier p. Les diviseurs de n sont 1 = p0, p, p2, ..., pα = n. Leur somme est :

Par exemple : la somme des diviseurs de 2n est 1 + 2 + 4 + 8 + ... + 2n = 2n+1 - 1
Soit maintenant n admettant deux facteurs premiers, sa décomposition en facteurs premiers s'écrivant pα × qβ. Les diviseurs du type pi sont 1, p, p2, ..., pα = n et ceux de type qj sont 1, q, q2, ..., qβ. Les autres diviseurs du type pi × qj s'obtiennent par combinaisons, et sans répétitions puisque p et q sont distincts. Leur somme est :
On voit donc que :
σ(pα × qβ) = σ(pα) × σ(qβ)
Si n admet trois facteurs premiers, le même raisonnement s'applique et en vertu de la formule de sommation :
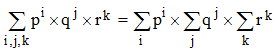
D'une façon générale, si n = p1α × p2β × ... × pkγ est la décomposition en facteurs premiers d'un entier n non premier, la somme de ses diviseurs (y compris 1 et lui même) est le produit :
σ(n) = (1 + p1 + p12 +... + p1α) × (1 + p2 + p22 +... + p2β) × ... × (1 + pk + pk2 +... + pkγ)
C'est à dire :

➔ Si m et n sont premiers entre eux, alors m et n n'ont aucun diviseur premier commun et par conséquent :
σ(m × n) = σ(n) × σ(n)
Par exemple : la somme des diviseurs de 80 = 5 × 16 = 5 × 24 est σ(80) = σ(5) × σ(24) = 6 × (25 - 1) = 6 × 31 = 186. On vérifie que les diviseurs sont obtenus en combinant{1,2,4,8,16} à {1,5}, soit 1,2,4,8,16,5,10,20,40,80 dont la somme est 186.
Somme des diviseurs et nombres parfaits : »
∗∗∗ Quelques exercices résolus
a) Un entier naturel n possède 5 diviseurs. Est-ce possible ?
Oui, 5 étant un entier premier,
le produit ci-dessus, fournissant le nombre de diviseurs, est réduit à un seul facteur (α+1) =
(4 + 1); n est donc de la forme p4 où p est premier. Le plus petit
entier n est donc 16, puis 81, etc.
b) Un entier naturel n possède 6 diviseurs. Quelle est la forme
de ces nombres ?
6 n'est pas premier, on peut écrire 6 = 2 × 3 = (1 + 1)(2 + 1), n peut donc être de la forme a × b2 avec a et b premiers. Par exemple : 75 = 3 × 52. Mais 6 peut aussi s'écrire 5 + 1, donc n peut également être de la forme p5, par exemple 32 = 25.
Une conjecture de Catalan : »
_______________
c) Déterminer les entiers n tels que n2 + 8n - 56 soit un carré parfait :
Remarquer que n2 + 8n - 56 = (n + 4)2 - 72; si ce nombre est un carré p2, alors (n + 4 + p)(n + 4 - p) = 72; rechercher tous les diviseurs de 72 et procéder par épuisement des cas en notant que n > 4...
_______________
d) Déterminer x et y afin que le nombre qui s'écrit "27x85y" (en base 10) soit divisible par 3 et par 11.
x + y + 1 doit être divisible par 3 et y - x + 8 doit être divisible par 11; x et y n'excédant pas 9, y - x + 8 ne peut excéder 17, donc y - x + 8 = 11; c'est dire que y - x = 3; procéder ensuite par épuisement des cas.... Vous devriez trouver deux solutions n = 271854 ou n = 274857.
e) Justifier que tout entier de la forme n3 - n, n entier naturel, est un multiple de 6.
n3 - n = n(n2 - 1) = n(n + 1)(n
- 1). Si deux nombres entiers sont consécutifs, l'un des deux est pair. Donc n3
- n est divisible par 2. On peut savoir que si trois nombres sont consécutifs,
alors l'un des trois est divisible par 3. Preuve : dans la division de n par 3,
n = 3q + r avec t r = 0, 1 ou 2. Si r = 0, n est divisible par 3; si r = 1, n - 1
= 3q est divisible par 3; si r = 2, n + 1 = 3q + 2 + 1 = 3(q + 1) est divisible
par 3. Le résultat est donc acquis : n3 - n est divisible par 2 et
par 3 donc divisible par 6 car 2 et 3 sont premiers entre eux.
! Attention, si
un nombre n est divisible par 4 et 6, il n'est pas assuré qu'il soit divisible
par 24 mais seulement par 12, plus petit multiple commun à 4 et 6, car 2
est un diviseur commun à 4 et 6 !
Si un entier n est divisible par a et b, alors n est divisible par ppmc(a,b)
PGCD et PPMC : »
∗∗∗ Exercices
élémentaires
Divisibilité par 3 et 5 ,
Division
euclidienne ,
Multiples & diviseurs
#2 , Multiples &
diviseurs #3
Les 3 filles
de mon voisin ,
Triangles dont les mesures des angles sont
des diviseurs de 360