
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|

On suppose que la Terre est une sphère parfaite de 6378 km de rayon.
1°/ En admettant une parfaite visibilité, jusqu'à quelle distance une personne dont le regard est placé à 2 m du sol pourrait-elle voir un point de la surface terrestre.
2°/ Vous êtes maintenant pilote à bord d'un AirBus A330 volant à 10 000 m d'altitude. Même question.
3°/ Du haut de la tour Eiffel (324 m en haut de son antenne), avec de fortes jumelles, par beau temps, pourrait-on voir la mer ?
Pour l'observateur P, le point visible le plus éloigné (à l'horizon) est le point de tangence de la demi-droite (virtuelle) issue de l'œil.
! Sur le schéma, les proportions ne
sont pas du tout respectées ! à bord d'un AirBus à 10 km d'altitude, une figure
à l'échelle,
pour un rayon de la Terre de 4,5 cm comme ci-dessous, donnerait une
distance PA égale 0,07 mm...

O désignant le centre de la Terre, le rayon [OH] est alors perpendiculaire à [PH) et il suffit d'appliquer le théorème de Pythagore dans le triangle rectangle OHP : on a PH2 = OP2 - OH2, soit, en notant h la hauteur de vue de l'observateur :
PH2 = (R + h)2 - R2
♦1°/ A 2 m d'altitude, on aura PH2 = (R + h)2 - R2 = 6378,0022 - 63782 = 25,512, ce qui fournit, en prenant la racine carrée :
PH ≅ 5,05... km, arrondi à 5 km.
♦2°/ A 10 000 m d'altitude, on a AK'2 = 63882 - 63782, ce qui fournit :
AK' ≅ 357, 29... km, arrondi à 357 km.
➔ Remarquer que l'on a ici : cos ^AOK' = OK'/OA = R/(R + h), soit ^AOK' ≅ 3,2° (non respecté sur la figure comme déjà dit ci-dessus). Cela correspond sur Terre à une distance PK' ≅ 2πR × 3,2/360 ≅ 40 074 × 3,2/360 ≅ 356 km à compter de la verticale du lieu : sensiblement la même valeur qu'à 10 km d'altitude.

à bord d'un satellite géostationnaire (météo, GPS, Télévision) situé à 36 000 km d'altitude (35785 km pour être plus précis), les proportions sont inversées et on ne peut pas assimiler AK et PK : cos ^AOK = OK/OA = 6378/42163, soit ^AOK ≅ 81,3°, proche de 90°! le satellite "arrose" donc presqu'un hémisphère ! Cela correspond sur Terre à un arc PK d'environ 9033 km ou KK" = 18066 km.
Un tel satellite est situé dans un plan équatorial. C'est dire que selon notre calcul, il ne voit cependant aucun point terrestre de latitude nord ou sud excédant 81,3°. L'angle ^OAK mesure alors 8,7° environ. Plus S s'éloigne, plus cet angle diminue.
Si S est à l'infini, il est nul : tout se passe comme si (SK) et (SK") étaient parallèles (deux droites parallèles se coupent à l'infini) et la Terre apparaît alors comme un disque. Le Soleil, situé à environ 150 millions de km, apparaît pour nous comme un disque car l'angle ^OSK (parallaxe) est extrêmement petit (8,8 secondes d'angle ≅ 0,0024°) : ses rayons nous semblent parallèles.

Calcul du rayon de la Terre : ›››› Distance Terre-Lune : ››››
♦3°/ A 324 m d'altitude, on a PH2 = 6378,3242 - 63782, ce qui fournit : AK ≅ 64, 3... km, arrondi à 64 km. Ce n'est pas assez haut pour voir la mer car en consultant une carte, on constate que Paris est à environ 150 km à vol d'oiseau (le plus proche étant l'estuaire de la Seine) et, à cette très faible altitude, on peut assimiler la distance PH à l'arc pH : la mer est encore loin derrière H !
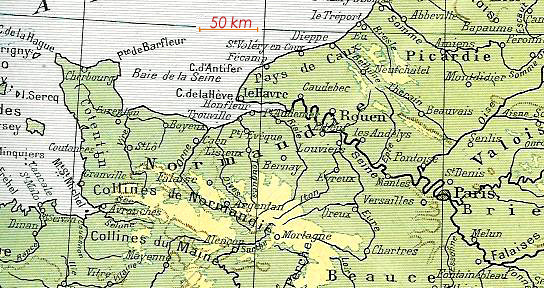
extrait Carte de France physique (Larousse XXè
siècle - 1930)