ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

La logique d'Aristote

Outre la notion de syllogisme, on doit à Aristote les acceptions actuelles du vocabulaire (cadre jaune) lié au raisonnement déductif (on parle aussi de raisonnement hypothético-déductif), exposées dans les Topiques et dans ses traités sur la logique, Les Analytiques, La métaphysique :

C'est chez Aristote que l'on trouve pour la première fois un langage propositionnel du type :

si P alors Q

et des lettres utilisées pour exprimer des propositions non explicitées. Une proposition est une affirmation (énonciation) du type « A est B » : A est le sujet (ce dont on parle) et B le prédicat (du latin praedicare = proclamer, qui a donné prêcher), attribut qui peut être affirmé ou nié.

• « Tout homme est mortel », « Cet enfant a les yeux bleus », « 124 n'est pas multiple de 3 » sont des propositions. La seconde peut cependant porter à controverse sur l'appréciation de la couleur. On parle parfois à tort de prédicat pour désigner une proposition.

Autre sens, plus récent, de prédicat (fonction propositionnelle) : »

La logique propositionnelle d'Aristote est le premier exposé de logique formelle, c'est à dire susceptible d'établir les lois universelles qui régissent notre pensée indépendamment de son contenu, mais qui s'avéra un socle insuffisant face à l'évolution des mathématiques.

Cette logique basée sur le VRAI et le FAUX connut, dans les années 1930, quelques soucis avec l'apparition de propositions indécidables et la vague intuitionniste de Brouwer. Le raisonnement déductif use essentiellement des conjonctions et adverbes ET, OU, SI, ALORS auxquels s'ajoute la négation (NON). Pour la rigueur du raisonnement de l'esprit humain, il s'agit d'en donner un sens précis, ce que fit en particulier de Morgan au 19è siècle.

Voici les connecteurs (1 à 3) et principes fondamentaux (4 et 5) de la logique d'Aristote, en usage de nos jours, sur lesquels sont fondés les lois, et règles fondamentales du raisonnement logique.

1. Connecteur (binaire) de conjonction (ET) :

P et Q étant deux propositions, on appelle conjonction de P et de Q, l'énoncé « P et Q » souvent noté P ∧ Q (notation de Russel).

• P : « x est un entier naturel pair », Q : « x est un entier naturel divisible par 3 »
  P ∧ Q : « x est un entier naturel multiple de 6 ».

2. Connecteur (binaire) de disjonction (OU) : 

P et Q étant deux propositions, on appelle disjonction de P et de Q, l'énoncé « P ou Q » souvent noté P ∨ Q (notation de Russel). Ce ou est inclusif : ce n'est pas un ou bien (ou exclusif), P et Q peuvent coexister. Par exemple :

• Dans un plan rapporté à un repère (O, Ox, Oy), Soit M(x,y). Si P : « M ∈Ox », Q : « M ∈Oy » alors P ∨ Q : « M(x,y), xy = 0 ».

• Concernant l'exemple donné pour ET précédent, P ∨ Q signifie « n est divisible par 3 ou n est pair ». Autrement dit, rien de mieux... Mais on remarque que n peut égaler 6 : le "OU contient le ET", tout comme la réunion de deux ensembles contient leur intersection.  » Cantor  

3. Connecteur (unaire) de négation (NON) :

Énoncer la négation d'une proposition P, notée ici nonP (mais on rencontre très souvent ¬P ou P ou, anciennement ~P à l'instar de Peano et Russel) consiste à prendre le contre-pied de P :  on énonce le contraire. Si P est vraie, nonP est fausse et vice versa.

• Si P s'énonce « tout nombre entier divisible par 2 est divisible par 4 », nonP peut s'énoncer « il existe au moins un nombre entier divisible par 2 qui n'est pas divisible par 4 ». C'est nonP qui est vraie : preuve en  l'entier 6.

 ➔  Dans l'exemple ci-dessus, l'introduction de l'entier 6 non divisible par 4 s'appelle un contre-exemple : en exhibant cet entier, on montre de façon très simple la fausseté de P. Dans l'art de la démonstration, un bon contre-exemple vaut souvent mieux qu'un long discours... Voici deux contre-exemples célèbres de l'histoire des mathématiques :

Contre-exemple d'Abel : »             Contre-exemple de Weierstrass : »

∗∗∗
Justifier par une argumentation élémentaire que (lois d'Abraham de Morgan): 
non(P ∧Q) signifie nonP ∨nonQ   et (dualité) :  non(P ∨Q) signifie nonP ∧ nonQ

4. Le principe de non contradiction :

Si P désigne une proposition, P et non P ne peuvent coexister. En d'autres termes P et nonP ne peuvent être toutes deux vraies :

non(P ∧ nonP)

5. Le principe du tiers exclu (en latin tertium non datur) :

Si P désigne une proposition, alors P ou bien nonP est vraie

Le principe de non contradiction énoncé précédemment permet d'énoncer simplement :

P ∨nonP

 ➔  Le ou (∨) ci-dessus est implicitement exclusif puisque P et non P ne peuvent coexister. Le principe du tiers exclu n'admet donc pas l'indécidabilité. Il sera contesté au 20è siècle par Brouwer pour les domaines infinis, dans le cadre de l'intuitionnisme. On peut résumer les deux principes de contradiction et du tiers exclu par :

P et nonP ne peuvent coexister et si l'une est vraie, l'autre ne l'est pas.   (nc_te)

Avant le et c'est le principe de non contradiction, après le et c'est le principe du tiers exclu. Comme l'écrit Ferdinand Gonseth dans ses Fondements des mathématiques (1926) : "ces deux principes n'en forment au fond qu'un seul. Le parfait contradictoire ne prend sa véritable signification que par le principe du tiers exclu".

En effet, selon les lois de de Morgan, non(P ∧ nonP) n'est autre que nonP ∨ non(nonP), c'est à dire nonP ∨ P, autrement dit le principe du tiers exclu.

6. non(nonA) est A :

En admettant les principes 4 et 5 en tant qu'axiomes de la logique propositionnelle : A et nonA sont contradictoires, il en est donc de même de nonA et non(nonA) et, par tiers exclu, il vient que non(nonA) exprime A : non(nonA) ⇔ A : cette tautologie (au sens logique : vraie que A soit valide ou non) est donc un théorème issu des deux axiomes, conséquence de l'acceptation du principe de tiers exclu.

7a. Connecteur d'implication logique (SI ... ALORS) également dit d'inférence :

La notion d'inférence logique se rencontre déjà dans l'Encyclopédie de Diderot et d'Alembert. Notée P ⇒ Q depuis Bourbaki, elle s'exprime par si P alors Q. L'implication logique est à la base de tout raisonnement mathématique ou non. On peut l'exprimer au moyen des trois connecteurs fondamentaux par :

(P ⇒ Q) signifie (nonP ∨ Q)

Cette définition formelle n'est pas simple à accepter car il faut admettre, comme étant logique, que si P s'avère fausse l'implication P ⇒ Q, en tant que proposition composée, est vraie et cela, que Q soit vraie ou fausse ! On dit parfois que le faux implique le vrai. A tort a priori, car d'une hypothèse fausse on ne peut en fait rien déduire, mais dans le cadre de la logique formelle (théorie abstraite de l'inférence), une proposition non réputée fausse est vraie (» tiers exclu). Toutefois :

Il vous paraît sans doute naturel d'exprimer que non(P ⇒ Q) n'est vraie que si P est vraie et Q fausse. autrement dit, non(P ⇒ Q) signifie (P ∧ nonQ). Dans ces conditions, et en utilisant les lois de Morgan étudiées en exercice, P ⇒ Q signifie non(P ∨ Q).

• Soit P : « n est divisible par 3 » et Q : « n est divisible par 6  ». On a Q ⇒ P mais (P ⇒ Q) est fausse : non(P ⇒ Q) est vraie.

On trouvera sur la page consacrée à Frege une seconde approche de ce connecteur d'implication.

 ➔  La notation utilisée ici pour l'implication est celle de Bourbaki, dès 1948. On utilisa aussi la flèche simple → (comme Hilbert) ainsi que le signe ⊃signifiant la contenance dans le langage des ensembles)

7b. Règle de transitivité : [(P ⇒ Q) ∧ Q ⇒ R] ⇒ (P ⇒ R).

 ➔  Lien analogique : cette propriété fondamentale de l'implication se retrouve dans la structure d'ordre. Tout comme celle de réflexivité P ⇒ P, équivalente au principe du tiers exclu (§8) et on peut aussi parler, avec l'équivalence logique ci-dessous, d'une antisymétrie, l'équivalence logique remplaçant alors l'égalité.

∗∗∗
1. Montrer que (P ∨Q) ∧ nonQ  ⇒ P
Montrer que le principe du tiers exclu se résume à : P ⇒ P.

7c. Implication et syllogisme :

Le syllogisme aristotélicien illustré par :

Tous les hommes sont mortels, or Socrate est un homme donc Socrate est mortel

peut s'écrire comme une tautologie (vraie quelle que soient la véracité ou la fausseté des propositions entrant en jeu) au moyen des connecteurs  ⇒ (implique) et ∧ (conjonction) : [("homme" ⇒ "mortel") ∧ "homme"] ⇒ "mortel" et plus généralement :

[P ⇒ Q) ∧ P ] ⇒ Q

ET (∧), OU (∨) et lois de Morgan : »            Logique des prédicats de Frege basé sur les connecteurs ⇒ et ¬ : »

8. Connecteur d'équivalence,  locutions "si et seulement si" et "il faut et il suffit" :

Deux propositions P et Q sont sites équivalentes et on note P ⇔ Q, lorsque (P ⇒ Q) ∧ (Q ⇒ P). Dans un raisonnement logique, deux de telles propositions peuvent se remplacer mutuellement.

• Soit P : « n est un entier divisible par 10 » et Q : « n est un entier dont le chiffre des unités est 0 ». On a P ⇔ Q.

 !   Le si et seulement si est souvent synonyme d'erreur... Considérons les énoncés :

1. « si un entier n est divisible par 10, alors n se termine par 0 »;

2. « un entier n est divisible par 10 si n se termine par 0 »;

3. « un entier n est divisible par 10 si et seulement si n se termine par 0 » ?

Soit P : « n est divisible par 10 » et Q : « n se termine par 0  ».

• Le cas 1 : P ⇒ Q : c'est l'implication usuelle si ... alors.

• Le cas 2 : il s'agit de Q ⇒ P, Q est une condition suffisante pour P : si n se termine par 0, alors n est divisible par 10. Mais cet énoncé est mal exprimé, on devrait toujours écrire si ... alors.
   ➔  A ce stade, on peut donc affirmer que P ⇔ Q, conjonction de P ⇒ Q et Q ⇒ P.

• Le cas 3 : P ⇔ Q. Le si suivant le 10 correspond à Q ⇒ P et apparaît comme condition suffisante avec le sens de dès que : un nombre n est divisible par 10 si (dès que) n se termine par 0.
  Le seulement si correspond à P ⇒ Q et apparaît comme condition nécessaire avec le sens de à condition que : un nombre n est divisible par 10 seulement si (à condition que) n se termine par 0.

   ➔  Dans le cas 1, on peut aussi dire que P est nécessaire pour Q : si n n'est pas divisible par 10, alors n ne se termine pas par 0. On peut se convaincre de :

  (P ⇒ Q)  ⇔ (nonQ ⇒ nonP)        » proposition contraposée

  Ces exemples donnent un sens à l'expression il faut et il suffit exprimant une condition à la fois nécessaire (P ⇒ Q) et suffisante (Q ⇒ P).

 i  Dans ChronoMath, afin d'abréger ou de simplifier des énoncés
le si et seulement si est souvent remplacé par l'abréviation soulignée ssi.

9. Le raisonnement par l'absurde :

Explicité dans les Topiques, le raisonnement par l'absurde ou réduction à l'absurde est un axiome fondamental de la logique aristotélicienne. Il voit sa consécration dans la preuve (Premiers Analytiques, Livre II) de l'irrationalité de la racine carrée de 2, résultat déjà prouvé, aux dires même d'Aristote, par les Pythagoriciens. Mais antérieurement à Aristote et à son maître, Platon, on n'a pas de trace écrite de démonstration. Ce très important résultat est aussi présent chez Euclide dans son livre IX des Éléments.

• Soit un énoncé de la forme H (hypothèses) ⇒ C (conclusion), dont on veut démontrer la véracité.

• Nions la conclusion C en admettant nos hypothèses H valides. On a donc : H et nonC.

• Supposons que cette conjonction de H et nonC nous amène (implication) à une contradiction (absurdité) : H et nonC est donc faux, sa négation, à savoir nonH ou C, est alors vraie (tiers exclu).

• Or H est valide, donc nonH est faux et par suite, c'est C qui est vraie.

Lois d'Abraham de Morgan : »

Appliquons le raisonnement par l'absurde exposé ci-dessus à la non rationalité de la racine carrée de 2, c'est à dire √2 n'est pas une fraction, résultat qui avait gravement troublé la belle harmonie des nombres des pythagoriciens...

• Soit H la proposition « x est la racine carrée de 2 : x² = 2 » et C : « la racine carrée de 2 n'est pas un nombre rationnel ».

• Supposons nonC, à savoir la racine carrée de 2 est un nombre rationnel.

• Cette racine carrée peut alors s'écrire comme fraction irréductible a/b vérifiant alors a² = 2b² (toute fraction est simplifiable jusqu'à la rendre irréductible : il suffit de diviser a et b par leur pgcd). Le carré de a étant pair, a est lui-même pair, donc de la forme 2n; il suit alors que le carré de b est 2n² et par là que b lui-même est pair :

• Absurde car a/b est irréductible : nonC induit donc une contradiction.

• En conséquence, C est valide (tiers exclu) : la racine carrée de 2 n'est pas un nombre rationnel.

On dira que le côté d'un carré et sa diagonale sont incommensurables ou que la diagonale d'un carré est incommensurable à son côté : voir alinéa suivant. Voir aussi ci-après un raisonnement par anthyphérèse.

Irrationalité de √2 par descente infinie : »

 ➔   Le raisonnement par l'absurde, comme le raisonnement par récurrence a ses limites : en effet, par manque d'information ou d'intuition, on n'est pas toujours en mesure de formuler le résultat escompté... D'autre part ce type de raisonnement s'avère invalide pour les intuitionnistes car ils réfutent l'équivalence logique, non(nonA) ⇔ A, évoquée ci-dessus par rejet du principe du tiers exclu.

On montrerait de même que √3 est irrationnel et plus généralement que toute racine carré d'un entier naturel premier p est irrationnel en remarquant que tout nombre non multiple de p est de la forme np + k où n et k sont entiers naturels, 0 < k < p.

La notion de grandeur :   

Tout chose (objet, concept ou phénomène, inerte ou vivant) possède des caractéristiques qualitatives et quantitatives. Par qualitatives, on entend par exemple sa forme, sa couleur, sa nature (solide, liquide, gazeux), sa constitution (bois, métal, alliage). à certaines de ces qualités, on peut associer un caractère quantitatif exprimant leur quantité dans l'objet en question. Depuis l'Antiquité, c'est ce caractère quantitatif, à savoir un nombre, que l'on appelle grandeur, quoique aujourd'hui suranné. Il correspond de nos jours à ce qu'on désigne par mesurable, quantifiable. Ce qui induit la notion d'unité de mesure (» alinéa suivant).

Deux grandeurs sont dites commensurables (mot à mot : mesurables ensemble) pour signifier qu'elles possèdent une mesure commune tout comme au sens moderne de la théorie de la mesure. Cette notion, théorisée par Euclide dans le livre X de ses Éléments remonte à Pythagore. Plus précisément :

Deux grandeurs a et b sont commensurables s'il existe une unité de mesure u et des entiers m et n
tels que a = n × u  et  b = m × u

En d'autres termes, a et b sont commensurables dès que l'une des trois assertions ci-dessous est vérifiée :

1. a et b sont des multiples d'une même unité.

2. il existe des entiers m et n tels que m × a = n × b.

3. le rapport a/b peut s'exprimer sous la forme d'une fraction n/m. L'unité est alors u = a/n = b/m.

Sinon, les grandeurs sont dites incommensurables (non mesurables ensemble). On pourra dire également que a est incommensurable avec b (et vice versa).

 ➔   Dans le cas de la diagonale d d'un carré de côté c, d et c seront commensurables s'il existe des entiers m et n tels que m × c = n × d avec, eu égard à la propriété de Pythagore : c² + c² = 2c² = d². Par suite m² = 2n², ce qui est impossible comme prouvé ci-dessus, ou ci-dessous (géométriquement) par anthyphérèse et encore ici (arithmétiquement) par descente infinie à la manière de Fermat, méthode à rapprocher de l'anthyphérèse, basée sur le fait que toute partie non vide de N admet un plus petit élément.

 i  Il est dit ci-dessus des entiers : on aurait pu dire des fractions (nombres rationnels), nombres acceptés par les grecs de l'Antiquité. En effet, une unité u étant choisie, si a/b mesure le côté du carré (c'est à dire a/b × u) et si p/q peut mesurer sa diagonale, choisissons l'unité u' telle que u = u' × bq. Avec cette unité le côté est entier : a × q et la diagonale également : p × b.

• Si l'unité u est le centimètre, parler de 3/4 signifiera 3/4 × 1cm, soit 0,75 cm.

Les unités de mesure :     

Il s'agit de définir, pour une grandeur donnée, son unité (de mesure) à savoir la grandeur d'un objet de même nature pris comme référence. Les exemples fourmillent. Les grandeurs les plus connues, étudiées dès l'école primaire, sont :

• Les longueurs et distances, incluant largeurs et profondeurs, exprimées en mètres, (m) centimètres (cm), mm (millimètres),  kilomètre (km), ...

• Les aires exprimées en mètres carrés (m²), centimètres carrés (cm²), millimètres carrés (mm²), ares (a, 100 m²), hectares (ha = 10 000 m² = 100 a), ...

 !   1cm² est l'aire c² d'un carré de côté c = 1 cm = 0,01 m. Donc 1cm² = 0,0001 m², soit un dix-millième de m² et non pas un centième comme pourrait le laisser penser l'appellation "centimètre carré". Erreur usuelle des jeunes élèves...

 !   Autre erreur souvent rencontrée : c'est quoi 100 m² ? Il s'agit de l'aire d'un carré qui, exprimée en m², est 100. L'aire d'un carré de côté c est c². Or, 100 = 10 × 10 : 100 est donc l'aire d'un carré de côté 10 et surtout pas un carré de côté 100 !

• Les volumes exprimés en mètres cubes (m³), centimètres cubes (cm³), millimètres cubes (mm³), ...

 !  Comme précédemment, attention : 1mm³ est le volume c³ d'un cube de côté 1 mm = 0,001 m. Donc 1mm³ = 0,000000001 m³, soit un milliardième de m³ et non pas un millième !

• Les capacités exprimées en litres (l), décilitres (dl, un dixième de litre), centilitres (cl, un centième de litre), ...

• Les poids exprimés en grammes (g), kilogrammes (kg = 1000 g), hectogrammes (hg = 100 g), tonnes (1000 kg), ...

• Le temps (concept) exprimé en secondes (s), minutes (min = 60 s), heures (h = 60 min), jours (j = 24 h), année (365 j);

• La mesure des angles exprimée en degrés d'arc, minutes d'arc, secondes d'arc, en grades ou en radians;

• La température (concept) exprimé en degrés Celsius (°C) ou Fahrenheit (°F).

• ...

De nouvelles grandeurs ont vu le jour avec le progrès scientifique et l'apparition de technologies récentes. Par exemple :

• La puissance électrique exprimée en watts (W), kilowatts (kw, 1000W);

• L'année lumière : distance parcourue par la lumière en 1 an (365 jours);

• L'aptitude au raisonnement logique (concept) se mesure, on parle de QI : le fameux quotient intellectuel dont 120 est une bonne moyenne;

• La violence d'un tremblement de Terre (phénomène) avec la fameuse échelle de Richter graduée de 0 à 9 (Charles Francis Richter, géophysicien américain, 1900-1985);

• La vitesse de fonctionnement d'un ordinateur (Mégahertz : Mhz) ou encore sa capacité mémoire (Mégabyte ou, en français, mégaoctet : Mo = 1024 kilo-octets = 1024 × 1024 octets);

• ...

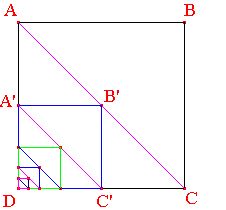On peut montrer que la diagonale et le côté d'un carré ne sont pas commensurables en procédant par anthyphérèse (du grec anthy = à son tour, tour à tour et aphairesis = action d'enlever, supprimer), raisonnement souvent employé par Euclide, proposition 1 de son livre X développant la notion de grandeur évoquée ci-dessus, également appelé axiome d'Archimède :

Deux grandeurs inégales étant données, retranchons de la plus grande une partie plus grande que sa moitié et retranchons du reste une partie plus grande que sa moitié; en faisant ainsi de suite, il restera une grandeur plus petite que la plus petite des deux grandeurs initiales.

Considérons un carré ABCD de côté AB, une de ses diagonales est AC.

Supposons AB et AC commensurables : il existe une unité u tel que AB = c × u et AC = d × u, avec c et d entiers. On a alors d² = c² + c² = 2c². Par suite, mesurés par u, d et c sont pairs. Si deux nombres sont commensurables, leurs moitiés le sont aussi. Enlevons au carré la moitié de son côté. La propriété s'applique alors au carré A'B'C'D de côté A'B' = c' = c/2 de diagonale A'C' = d' = d/2 :  c' et d' entiers et pairs. Au bout d'un certain nombre d'itérations, on finira par obtenir un côté entier inférieur à u, ce qui n'est pas possible : l'unité serait plus grande que la longueur (multiple de u) mesurée !