ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 

Vous trouverez ici les solutions d'une grande partie des exercices rencontrés dans l'ensemble des pages de ChronoMath repérés par le petit logo ∗∗∗ indiquant un exercice d'application d'un résultat ou d'une définition.

Des exercices ou problèmes plus élaborés peuvent être consultés à partir de la page d'accueil du site,
rubrique EXOS CLG/LYC/SUP.

 On considère la suite (f_n) de fonctions numériques continues définies pour tout réel x et tout n de N par :

f_o(x) = 1, f_n+1(x) = 1 + ∫_[o,x] [f_n(t)]²dt

a) Déterminer les fonctions f₁ et f₂.
b) Montrer que la suite (f_n) est un polynôme de degré 2ⁿ - 1
c) Montrer que les coefficients du polynôme f_n sont tous éléments de [0,1].
d) On suppose x appartenir à ]-1,1[, montrer que la suite (f_n) est convergente et que sa limite y est la solution de l'équation différentielle y' = y².

a) f₁(x) = 1 + ∫_[o,x] 1² dt. = 1 + x.
   f₂(x) = 1 + ∫_[o,x] (t + 1)² dt. = 1 + x + x² + x³/3

 i  f₃(x) = 1 + ∫_[o,x] (t + 1)² dt. = 1 + x + x²  + x³ + 2x⁴/3 + x⁵/3 + x⁶/9 + x⁷/63

b) d°(f₁) = 1 = 2¹ - 1; d°(f₂) = 3 = 2² - 1. On est en droit de poser d°(f_n) = 2ⁿ - 1; s'il en est ainsi, par définition de f_n+1, son degré est le double de celui de f_n augmenté de 1 par l'intégration, soit 2(2ⁿ - 1) + 1 = 2ⁿ⁺¹ - 2 + 1 = 2ⁿ⁺¹ - 1.
La formule étant vérifiée pour n = 1, elle est vraie pour tout n de N.

c) On remarque que f₂ (x) - 1 est un polynôme sans terme constant (nul en x = 0) dont les coefficients sont positifs, inférieurs ou égaux à 1. Par récurrence, on prouvera facilement qu'il en est de même, pour tout n des f_n+1(x) - 1 = ∫_[o,x] [f_n(t)]²dt, primitives nulles en 0 des f_n, car, par intégration, un monôme a_px^p devient a_px^p+1/(p+1), son coefficient devient donc a_p/(p+1) < a_p.

d) f_n(x) est un polynôme de degré N = 2ⁿ - 1 pouvant s'écrire, pour tout |x| < 1, Σ_p=0..N a_px^p. Les a_p étant positifs inférieurs à 1,|f_n(x)| ≤ Σ_p=0..N |x|^p. Cette somme n'est autre que la somme partielle de la série géométrique de raison  |x| convergente puisque |x| < 1. On en déduit que f_n(x) converge également et que sa limite est inférieure à 1/(1 - x).

D'autre part, pour n infini, lim f_n+1 = lim f_n. Soit y cette limite, fonction de x; On a y = ∫_[o,x] y²dt, primitive nulle en 0 de y². Ce qui signifie que y est dérivable et et que sa dérivée vérifie y' = y².

On aurait pu utiliser le théorème de Picard pour traiter cette question d). En effet, la fonction x → f(x,y) = y² est lipschitzienne sur l'intervalle ]-1,1[ :

|y²(x) - y²(x')| = |y(x) + y(x')| × |y(x) - y(x')| ≤ 2 |y(x) - y(x')|

donc la suite y_n+1(x) = 1 + ∫_[o,x] [y_n(t)]²dt converge et on a à la limite dy/dx = y².

 Déterminer la (les) fonction(s) numérique(s) vérifiant xf(x) + f(1 - x) = x² pour tout x réel.

Le changement de x en 1 - x conduit à (1 - x)f(1 - x) + f(x) = (1 - x)². D'où l'idée de considérer le système d'inconnues f(x) et f(1 - x) défini par ces deux relations. Le déterminant est x - x² - 1 = -x² + x - 1 ≠ 0 quel que soit x réel. On peut donc calculer f(x) sans ambiguïté. On trouvera facilement :

On pourra vérifier que ce résultat est bien la solution du problème en remplaçant f par son expression dans la relation de l'énoncé.

   Prouver que toute suite numérique strictement croissante et non majorée tend vers +∞. De même, toute suite numérique strictement décroissante et non minorée tend vers -∞.

Si (u_n) est majorée, alors il existe un réel A tel que, quel que soit n : u_n ≤  A. Par conséquent, (u_n) non majorée signifie : quel que soit le réel A, il existe n tel que u_n > A. Le nombre A pouvant être choisi arbitrairement grand, le résultat est établi à condition d'admettre le concept d'infinitude par :

• x est dit infini positif  si et seulement si  quel que soit A > 0, x > A.

• x est dit infini négatif si et seulement si  quel que soit A < 0, x < A.      » droite achevée

   Déterminer les fonctions numériques dérivables vérifiant f(x + y) = f(x) + 2xy + f(y).

On note que le problème admet au moins une solution, à savoir la fonction x → x². Le 1er membre s'interprète comme une fonction g de deux variables, g(x,y) = f(x + y). La fonction f étant dérivable, on peut écrire, pour tout y réel : ∂g/∂x = f '(x) + 2y. De même, ∂g/∂y = 2x + f '(y). La permutation de x et y laisse le problème inchangé. On peut alors écrire ∂g/∂x = ∂g/∂y et on obtient, pour tous x et y réels :  f '(x) = 2x - 2y + f'(y). Choisissons y = 0 et prenons les primitives de chaque membre :

f(x) = xf '(0) + x² + C, où C est une constante réelle a priori arbitraire

x = y = 0 dans f(x + y) = f(x) + 2xy + f(y) fournit f(0) = 0. Donc C = 0. Posons, pour simplifier f '(0) = a. On obtient f(x) = x² + ax.

Ce résultat étant obtenu par implication, nous devons vérifier si f est effectivement solution du problème. Le report de f(x) = x² + ax dans l'équation initiale se réduit à (x + y)f '(0) = xf '(0) + yf '(0) : la fonction f est solution. Noter que f '(0) = a.

  En admettant qu'une cubique (courbe algébrique de degré 3) puisse être définie par un polynôme réductible, montrer qu'une telle courbe peut contenir une conique.

Une cubique Q est définie algébriquement par une équation du type p(x,y) = 0 où p est un polynôme irréductible de degré 3 en x et y : elle est le lieu géométrique des zéros de p dans R². Si p n'est pas irréductible alors il est factorisable par un polynôme q du second degré en x et y qui s'annule sur Q : il existe un polynôme alors un polynôme r du 1er degré en x et y tel que p(x,y) = q(x,y) × r(x,y).

Voici un exemple : considérons Q définie par p(x,y) = 2x³ - y³ - 2x² + xy² + 2x² + y² - x + y - 1.

2x³ - y³ - 2x²y + xy² + 2x² + y² - x + y - 1 = 0

Dans cet exemple, "cousu de fil blanc", on peut écrire :

2x³ - y³ - 2x² + xy² + 2x² + y² - x + y - 1 = 2x²(x - y + 1) + y²(x - y + 1) - (x - y +1) = (2x² + y² - 1)(x - y +1)

Cette cubique apparait donc comme la réunion d'une ellipse et d'une droite : fausse cubique ! car la définition d'une courbe algébrique plane de degré donné exige un polynôme irréductible (non factorisable).

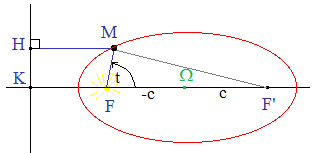
1°. Avec les notations usuelles MF + MF' = 2a (cas  b < a) de la définition bifocale, on pose MF = r. On désigne par t l'angle orienté ^(FF',FM). Prouver que : MF^'2 = r²  + 4c² - 4rc.cos t. Déduire de l'égalité MF + MF' = 2a que r = b²/(a - c.cos t).
2°. On pose p = b²/a. Retrouver l'équation polaire r = p/(1 - e.cost) et p = e × KF.

1°. On applique la formule d'Al-Kashi dans le triangle MFF' : MF'² = r² + 4c² - 4rc × cost. On a d'autre part MF'² = (2a - r)² = 4a² + r² - 4ar. En identifiant ces deux résultats, on obtient : 4c² - 4a² = 4r(c.cost - a), soit : r(a - c.cost) = a² - c² = b².

2°. L'identité r = b²/(a - c.cos t) peut s'écrire r = (b²/a) /(1 - (c/a).cos t). Or l'excentricité est e = c/a (cas b < a), d'où r = p/(1 - e.cost). D'autre part, on a, par définition de l'excentricité, e = MF/MH. Soit : e = MF/(KF + FN) = r/(KF + r.cost). D'où eKF + er.cost = r. Évaluons er.cost : on sait que r(1 - e.cost) = p, on en déduit er.cost  = r - p. Par suite eKF + (r - p) = r, soit e × KF = p.

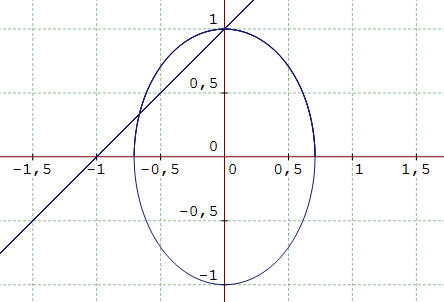
Par des considérations purement algébriques, montrer que l'origine O(0,0) est un point isolé de la cubique (C) définie par x² + y² + x³ + y³ = 0. Vérifier le bienfondé de ce résultat au moyen des dérivées partielles de f(x,y) = x² + y² + x³ + y³ au point O(0,0).

Il est clair que (C) contient O. Vue par Graphmatica, la courbe semble ne présenter aucun point autre que O dans le disque de centre O de rayon 1/2 < 1. Vérifions cela en remarquant dès à présent que dans ce disque, on a  0 < | x | < 1 et 0 < | y | < 1, donc :

 0 < | x³ | < x² < 1  et  0 < | y³ | < y² < 1    (r)

• Dans le 1er quadrant du disque (x > 0, y > 0), on a x² + y² + x³ + y³ > 0, donc aucun point de (C).

• Dans le 3è quadrant (x < 0, y < 0), on a x² + y² > 0,  x³ < 0 et y³ < 0. On a donc | x³ | = - x³ < x² et | y³ | = - y³ < y². Par conséquent x² + y² + x³ + y³ ne peut égaler 0.

• Dans le 4è quadrant (x > 0, y < 0), x² + y² + x³ + y³ = 0  ⇔  x² + y² +  | x³ | -  | y³ | = 0  ⇔  x² + y² =  | y³ | -  | x³ |. Donc si un point M(x,y) de (C) existe dans ce quadrant, on devrait avoir l'égalité :  | | y³ | -  | x³ | | = x² + y² =  | x² | +  | y² |.  Or, selon l'inégalité triangulaire et les relations (r) ci-dessus : | | y³ | -  | x³ | | <   | y³ | +  | x³ | < | y² | +  | x² |. Aucun point de (C) n'est présent dans le 4è quadrant.

• La courbe reste inchangée si on échange les rôles de x et de y. Par suite, aucun point de (C) n'est présent dans le 2è quadrant (x < 0, y > 0).

En utilisant les résultats généraux relatifs aux courbes définies par une fonction implicite f(x,y) = 0, on cherche à résoudre l'équation du second degré en m : m²∂²f/∂y² + 2m∂²f/∂x∂y + ∂²f/∂x²  = 0 où m désigne le coefficient directeur de la tangente au point considéré. Nous avons ici f(x,y) =  x² + y² + x³ + y³.

• ∂f/∂x = 2x + 3x²; ∂f/∂y = 2y + 3y²; ∂²f/∂x² = 2 + 6x; ∂²f/∂y² = 2 + 6y; ∂²f/∂x∂y = 0

• Outre f(x,y) = 0, un point singulier vérifie ∂f/∂x = ∂f/∂y = 0. Ce système conduit à O(0,0), les autres solutions ne correspondant pas à des points de la courbe.

• L'équation en m au point O se réduit à : 2m² + 2 = 0 : pas de solution, donc pas de tangente. O est donc un point isolé de (c).

  R étant considéré comme espace vectoriel sur lui-même. Toute application additive continue de R dans R est linéaire.

Soit f une telle application. On a donc pour tout x de R, f(x + y) = f(x) + f(y). En choisissant x = 0, on remarque que f(0) = 0, condition nécessaire à la linéarité. Il nous faut montrer que pour tout réel λ et tout x de R, f(λx) = λf(x)

1/  Considérons le cas f(nx), n∈N , x∈R

f(2x) = f(x + x) = f(x) + f(x) = 2f(x). Donc f(3x) = f(2x + x) = f(2x) + f(x) = 3f(x). On montre alors très simplement par récurrence que f(nx) = nf(x) pour tout n de N.

2/  Considérons le cas f(nx), n∈Z^- , x∈R

On remarque tout d'abord que f(x - x) = f(0) = 0 = f[x + (-x)] = f(x) + f(-x) : f est donc impaire. On peut écrire n = -|n| et on a |n|∈N. Donc f(nx) = f(-|n|x) = - f(|n|x) = - |n|f(x) = nf(x), l'avant dernière égalité étant due à 1/.

3/  Considérons le cas f(x/n), n∈N*

f(x) = f(nx/n) = f(n × x/n) = nf(x/n), donc f(x/n) = f(x)/n.

4/  Considérons le cas f(λx), λ∈Q

Si λ∈Q, alors λ = p/q, p∈Z, q∈N*. Donc f(λx) = f(px/q) = pf(x/q) = p/q × f(x) = λf(x).

5/  Considérons le cas f(λx), λ∈R

Tout réel λ est limite  d'une suite (λ_n) de rationnels pour laquelle on a donc f(λ_nx) = λ_nf(x). Pas suite :

• d'une part λ_nf(x) converge vers λf(x).
• D'autre part, la suite de terme général λ_nx converge vers λx. Par continuité de f, f(λ_nx) converge vers f(λx).

En conclusion f(λx) = λf(x), ce qui prouve que f est linéaire.

Montrer qu'un élément z de Z/nZ admet un inverse si et seulement si z et n sont premiers entre eux. En déduire que si n est premier, alors (Z/nZ ,+, × ) est un corps.

Dire que z est inversible dans Z/nZ signifie qu'il existe x dans {1,2, ..., n-1} tel que z × x = 1. Donc zx = 1 + kn, k ∈Z. D'où zx - kn = 1 : z et n vérifient l'identité de Bézout, il s'ensuit que z et n sont premiers entre eux.

Inversement, si pgcd(z,n) = 1, toujours selon Bézout, il existe u et v dans Z tels que uz + vn = 1. En passant aux classes d'équivalences, on obtient u × z + v × n = 1. Mais dans Z/nZ, n = 0. donc u × z  = 1 , ce qui montre que z est inversible et que son inverse est u.

En conséquence, si n est premier, tout élément z admet un inverse dans Z/nZ : cet anneau est donc un corps.

Rappel : la partie entière E(x) d'un nombre est ainsi définie : si n ≤ x < n + 1, n entier relatif (élément de Z), alors E(x) = n.

a) Montrer que dans le magma (Z,*) avec a * b = E(ab/6), E désignant la fonction partie entière, 6 est neutre et l'entier 2 admet trois symétriques.  » fonction partie entière.   b) Ce magma est-il associatif ?  

a) Recherchons e tel que a * e = a pour tout a de Z. E(ae/6) = a  ⇔  a ≤ ae/6 < a + 1. Pour tout a non nul au moins égal à 6, on a donc : 6 ≤ e < 6 + 6/a < 7. Donc si e existe, e = 6. Vérifions que e = 6 convient : a * 6 = a  ⇔  E(6a/6) = a  ⇔  E(a) = a. Cette dernière égalité est vérifiée pour tout entier relatif a. Ainsi 6 est neutre à droite; la loi étant manifestement commutative, 6 est neutre à gauche : 6 est l'élément neutre de la loi *.

La loi * étant commutative, on peut se contenter de rechercher les entiers b tels que 2 * b = 6. Cela revient à écrire E(2b/6) = 6, c'est à dire 6 ≤ 2b/6 < 7, ou encore 18 ≤ b < 21. Par conséquent 2 admet trois symétriques pour la loi *, à savoir 18, 19 et 20.

b) On a 2 * 18 = 2 * 19, donc 18 * (2 * 18) = 18 * (2 * 19); si le magma (Z,*) est associatif, il vient (18 * 2) * 18 = (18 * 2) * 19, c'est à dire 6 * 18 = 6 * 19, soit 18 = 19. Ce qui est faux, pas suite (Z,*) n'est pas associatif.

 ➔   Dans un magma associatif unifère, le symétrique d'un élément, quand il existe, est unique.  » loi de composition.

En utilisant l'algorithme d'Euclide, calculer le PGCD de 3046 et 45. En déduire une solution de l'équation 3046x - 45y = 5.

On a successivement :

3046 = 45 × 67 + 31  ;  45 = 31 × 1 + 14  ;  31 = 14 × 2 + 3  ;  14 = 3 × 4 + 2  ;  3 = 2 × 1 + 1

Ainsi 3046 et 45 sont premiers entre eux. On a alors successivement en "remontant" les calculs précédents :

• 1 = 3 - 2 × 1 = 3 - (14 - 3 × 4) = 3 × 5 - 14  = 5 × (31 - 14 × 2) - 14 = 5 × 31 - 11 × 14

• 1 = 5 × 31 - 11 × (45 - 31) = 16 × 31 - 11 × 45
• 1 = 16 × (3046 - 45 × 67) - 11 × 45 = 16 × 3046 - 1083 × 45

donc :

5 = 80 × 3046 - 5415 × 45 : une solution est x = 80, y = 5415

Paul, alors enfant, né au 20è siècle, avait calculé qu'en l'an 2000, son âge serait égal à la somme des chiffres de son année de naissance. En quelle année est-il né ?     (Bac C, Abidjan juin 1989)

Si l'année de naissance de Paul s'écrit 19ab, a désignant le chiffre des dizaines et b celui des unités et si A désigne l'âge de Paul en l'an 2000, vous devriez trouver A = 1 + 9 + a + b et A = 2000 - (1900 + 10a + b) puis 11a + 2b = 90. Pour résoudre cette équation, visitez cette page...

  On remplit une coupe conique à la moitié de sa profondeur. La coupe est-elle à moitié pleine ? Sinon à quelle hauteur doit-on la remplir ?

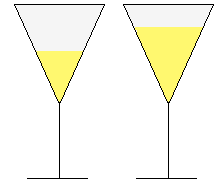Le volume intérieur de la coupe est V = πr²h/3. A mi-hauteur, selon la propriété de Thalès, le rayon est r/2; le volume est donc π(r/2)² × (h/2)/3 = V/8 : un huitième de la coupe... Pour obtenir la moitié de la coupe, notons h/k la fraction cherchée de la hauteur. Le rayon est dans le même rapport. Nous cherchons donc k tel que π(r/k)² × (h/k)/3 = V/2, c'est à dire :

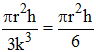
Par suite k³ = 2 et k = ³√2 (le symbole ³√ pour signifier racine cubique). En arrondissant cette racine cubique à 1,25 = 5/4. Il faut donc remplir le verre au 4/5è de sa profondeur !

  Construire à la règle et au compas (au sens d'Euclide) un triangle équilatéral ABC inscrit dans un cercle (c) préalablement tracé et dont on a seulement placé un sommet C ?

Analyse :   

Un triangle équilatéral est un polygone régulier. Si l'on suppose le problème résolu en considérant un triangle équilatéral ABC inscrit dans un cercle (c) de centre O; par raison de symétrie, la médiatrice de [AB] passe O et C, et est aussi la bissectrice de ^ACB. En plaçant sur le cercle (c) le point D tel que CO = CD, on fait apparaître le triangle équilatéral OCD (ses côtés sont des rayons) dont la bissectrice de l'angle C coupe le cercle (c) en B. Le sommet A sera obtenu sachant que BA = BC.

D'où la construction suivante qu'il s'agira de valider :

1. Le cercle de centre C passant par O coupe le cercle (c) en D et D';

2. On trace la bissectrice de l'angle ^OCD; elle coupe (c) en B.

3. Le cercle de centre C de rayon CB coupe (c) en A.

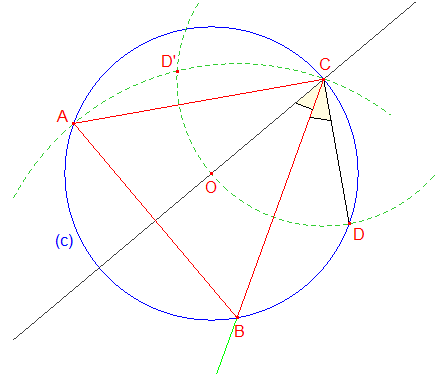
Synthèse :   

Le triangle ABC est équilatéral :

1. Par construction CA = CB : le triangle ABC est isocèle de sommet principal C;
   Par suite, (c) étant le cercle circonscrit à ABC : la médiatrice de [AB] passe par O et est bissectrice de l'angle principal ^C;
   On a donc ^ACO = ^BCO

2. Par construction CO = CD = OD : OCD est équilatéral et (CB) est la bissectrice de ^OCD;
   Par suite, ^BCO = 30° = ^ACO.

3. Le triangle isocèle ABC d'angle principal ^C de mesure 60° est donc équilatéral.

 ➔   Tout triangle isocèle admettant un angle de mesure 60° est équilatéral :

• S'il s'agit de l'angle principal, la somme des mesures des deux autres est 120°; ces angles ayant même mesure, le triangle est équilatéral;

• S'il s'agit d'un angle à la base, le second mesurant également 60°, il nous reste 60° pour la mesure de l'angle principal : le triangle est équilatéral.

  Existe-t-il dans N deux entiers a et b dont aucun n'est un carré tels que √a + √b soit entier ?

 Résoudre dans R, l'équation(e) :  ln |x² - 2| = 1

ln e = 1, donc ln |x² - 2| = 1 ⇔ ln |x² - 2| = ln e ⇔  |x² - 2| =  e     (a > 0, b > 0, ln a = ln b ⇔ a = b)
Par conséquent : (e) ⇔ |x² - 2| =  ± e    (|A| = k , k ≥ 0  ⇔ A = ± k). 

D'où : (e) ⇔ x² = 2 + e ou x² = 2 - e. Mais 2 - e < 0.
Les solutions de (e) sont donc x = ± √(2 + e)

 p1/ P admet x_o comme racine multiple de multiplicité k si et seulement si P(x_o) = 0 et x_o est un zéro d'ordre k - 1 pour le polynôme dérivé de P.

La condition est nécessaire : supposons P(x) = (x - x_o )^kQ(x). Donc P'(x) = k(x - x_o )^k-1Q(x) + (x - x_o )^kQ'(x) = (x - x_o )^k-1[kQ(x) + (x - x_o )Q'(x)]. Le crochet ne s'annule pas en x_o, sinon, Q s'annule en x_o et ce nombre serait un zéro d'ordre k+1 pour P. Par conséquent x_o est un zéro d'ordre k - 1 pour P'. La condition est suffisante : supposons que x_o soit un zéro d'ordre k - 1 pour P' et que P(x_o) = 0. Notons p l'ordre de x_o pour P; d'après ce qui précède, son ordre pour P' est p - 1. Donc p - 1 = k - 1, c'est dire que p = k.  CQFD

 p2/  P admet x_o comme racine multiple de multiplicité k si et seulement P(x_o) = 0 et les dérivées successives de P jusqu'à l'ordre k - 1 s'annulent en x_o, la dérivée k-ème n'étant pas nul.

La condition est nécessaire : d'après le résultat précédent, est d'ordre k - 2 pour P'', k - 3 pour P''' et finalement d'ordre 1 (racine simple) pour le polynôme dérivé (k -1)-ème, la dérivée k-ème n'est donc pas nulle. La condition est suffisante : supposons que x_o annule toutes les dérivées jusqu'à l'ordre k - 1 et soit p l'ordre de x_o pour P. On vient de montrer que la dérivée p-ème n'est pas nulle en x_o. D'après p1/ il vient p - 1 = k - 1; c'est dire que p = k.

 Représenter le graphe orienté défini par une matrice. Rappel de la matrice du graphe :

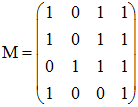
Le graphe étant orienté, nous plaçons un arc du sommet i vers le sommet j si l'élément a_i,j placé en ligne i, colonne j est égal à 1. On obtient donc :

L'arc BD du graphe ci-dessus rencontre l'arc AC dans cette première représentation. Cette intersection est virtuelle. En quelque sorte l'arc BD passe au-dessus (ou au-dessous) de l'arc AC : en déplaçant D comme ci-dessous, on obtient une représentation planaire :

• les sommets apparaissent distincts;

• les arêtes soient des courbes simples (pas de point double ou multiple);

• les arêtes ne se rencontrent qu'en leurs extrémité.

Dans le cas précédent, sans faire référence au graphe, donner le nombre de chemins de longueur 3 non triviaux (n'utilisant aucune boucle) reliant i/  A à C    ii/  B à D   iii/ C à C (circuits d'origine C). 

Afin d'éviter les chemins bouclés comme A → A → A → D ou A → D → A → D, il faut mettre à zéro les éléments de la diagonale de M et calculer la puissance troisième de la matrice M' obtenue :

• i/ La ligne 1, colonne 3 donne le nombre de chemins de A à C de  longueur 3 : 2 chemins

A → D → A → C , A → C → B → C

• ii/ La ligne 2, colonne 3 donne le nombre de chemins de B à D de  longueur 3 : 3 chemins

B → A → C → D , B → C → B → D , B → D → A → D

• iii/ La ligne 2, colonne 1 donne le nombre de circuits d'origine C : 2 circuits

C → D → A → C , C → B → A → C

Vérifier par déplacement des sommets que le graphe ci-dessous est planaire.

La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet. On peut simplifier le graphisme en remplaçant les arcs orientés simples ou doubles par des arêtes. Avant "nettoyage", vous pourriez obtenir ceci :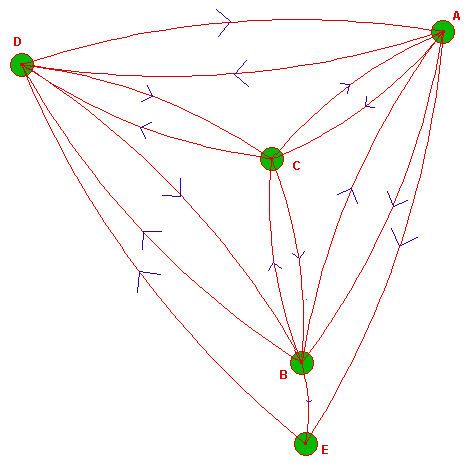

Si votre navigateur accepte les applets Java (» extension CheerpJ) :

Graphe après "nettoyage"; il vous sera facile de donner sa représentation planaire :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :

  Exercice extrait de : Problèmes de Mathématiques, classe de Math. Sup., par jean Taillé, Éd. Vuibert 1966)

On considère la matrice A définie par :

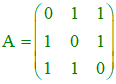
Calculer A² puis A² - A. En déduire que A est inversible et exprimer A^-1 en fonction de A et I.

On trouve aisément que :

I désignant la matrice unité :

On peut alors écrire : A × (A - I) = 2I. Autrement dit : A × ½(A - I) = I.

La matrice A admet donc pour inverse à droite la matrice ½(A - I). L'anneau des matrices carrées n'est pas intègre. Il faut donc vérifier que ½(A - I) est aussi inverse à gauche pour A (voir cet exercice), c'est à dire que ½(A - I) × A = I. Or A commute avec elle-même et I, donc avec ½(A - I) ; l'égalité est donc vérifiée et on peut écrire :

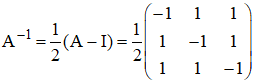
Questions complémentaires :     

q1) Selon les calculs précédents, on a A² = A + 2I. On pose alors u₂ = 1, v₂ = 2.
      Montrer par récurrence que l'on peut écrire Aⁿ = u_nA + v_nI avec u_n+1 = u_n + v_n , v_n+1 = 2u_n.

q2) On pose α_n+1 = 2u_n+1 + v_n+1 et β_n+1 = u_n+1 - v_n+1. Calculer α_n et β_n en fonction de n.

q3) En déduire u_n et v_n en fonction de n puis l'expression de Aⁿ en fonction de n.

q1) La formule est vérifiée pour n = 2 : A² = A + 2I avec u₂ = 1 , v₂ = 2. Supposons Aⁿ = u_nA + v_nI, n ≥ 2.

Aⁿ⁺¹ = (u_nA + v_nI) × A = u_nA² + v_nA = u_n(A + 2I) +v_nA = (u_n + v_n)A + 2u_nI

La formule de récurrence est donc vérifiée avec u_n+1 = u_n + v_n et v_n+1 = 2u_n.

q2) α_n+1 = 2u_n+1 + v_n+1 = 2u_n + 2v_n + 2u_n= 2(2u_n+ v_n) = 2α_n.
      β_n+1 = u_n+1 - v_n+1 = u_n + v_n - 2u_n = v_n - u_n = - β_n.

• La suite (α_n) est géométrique de raison 2, avec α₂ = 2u₂ + v₂ = 4 = 2α₁; d'où α₁ = 2 et α_n = 2ⁿ.
• La suite (β_n) est géométrique de raison -1, avec β₂ = u₂ - v₂ = -1 = - β₁; d'où β₁ = 1 et β_n = - (-1)ⁿ.

q3) On a 2u_n + v_n = α_n et u_n - v_n= β_n. Par addition, on en déduit 3u_n = 2ⁿ - (-1)ⁿ.
     Par soustraction en multipliant préalablement u_n - v_n= β_n par 2, on obtient 3v_n = α_n - 2β_n = 2ⁿ + 2(-1)ⁿ.
     Finalement, Aⁿ = u_nA + v_nI, c'est à dire :

Aⁿ = [2ⁿ(A + I) + (-1)ⁿ(2I - A)]/3

Et la formule s'avère exacte pour A¹ = A et A⁰ = I.

 1°/ Montrer que toute puissance n-ème d'une matrice stochastique est une matrice stochastique.
2°/ Vérifier qu'une matrice stochastique M admet le vecteur propre P =  (1,1,...,1) pour la valeur propre 1 : MP = P

Si M = p_i,j est une matrice stochastique, on a :

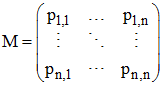
les p_i,j sont positifs et pour tout i = 1, 2, ...n :

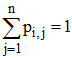
Si nous montrons que M stochastique M² stochastique, le résultat sera acquis par récurrence. Si nous montrons que la somme des éléments de la 1ère ligne de M² est égale à 1, le résultat sera acquis pour les autres lignes et le résultat cherché le sera aussi.

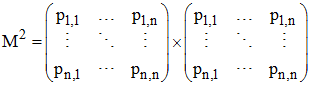
La somme des éléments de la 1ère ligne est :

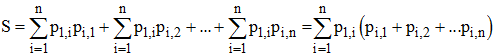
La parenthèse est égale à 1 puisqu'il s'agit de la somme des termes de la i-ème ligne de M. La somme S est donc égale à :

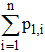
et cette somme est égale à 1 puisqu'il s'agit de la somme des termes de la 1ère ligne de M. La matrice M² est donc stochastique. CQFD.

Ce graphe complet, noté K5, K comme Kuratowski, est-il planaire ?

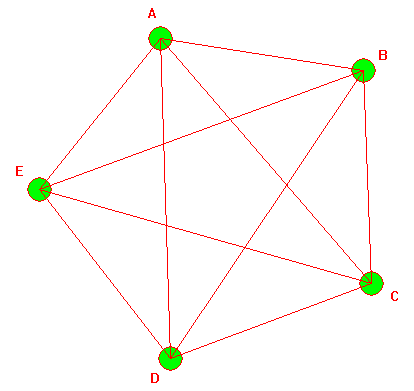
Ne cherchez pas plus longtemps, ce graphe n'est pas planaire ! Considérons la relation binaire R ainsi définie :

• X est l'ensemble des faces de G', Y sont ses arcs. On pose x R y si et seulement si y est une arête de la face x.

Le diagramme sagittal de R est un graphe Γ. Une arête de G' ne peut être commune qu'à deux faces au plus, Γ ne peut donc avoir au plus que 2a arêtes. Les faces de G' ont au moins trois arêtes et on a f faces, Γ possède donc au moins 3f arêtes.

Or, selon la formule d'Euler, on constate que si ce graphe possède une représentation planaire, son nombre de faces sera f = 2 - a - s = 7 car il a 5 sommets et 10 arêtes. Ce qui est fâcheux car nous devrions avoir, d'après ce qui précède, au plus 20 arêtes et au moins 21... : ce graphe complet, noté K5, en l'honneur de Kuratowski, n'est pas planaire. Rajouter un sommet à une intersection le rend planaire !

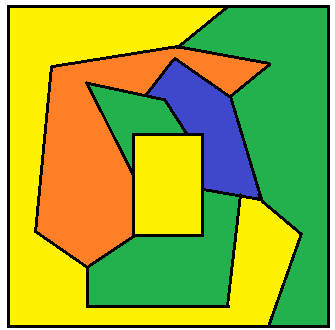
  Théorème des 4 couleurs; un exemple de solution :

 Placer un sommet à une intersection peut tout changer : vérifier par déplacement des sommets que le graphe ci-dessous est planaire.

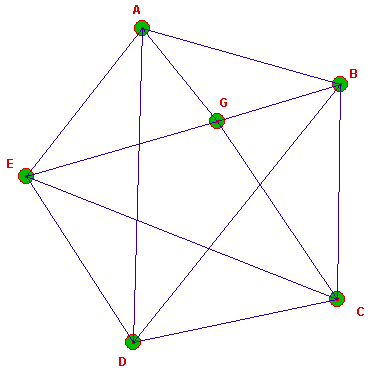
Solution : on sort du pentagone ABCDE le sommet G du graphe, on glisse D dans EABC et on "rétrécie" l'arête AB... :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :

  Résoudre les équations différentielles (e1) : y' = -x/y, y ≠ 0  et  (e2) : xy" = 2y'.

e1) Cherchons les solutions y = f(x) sur tout intervalle I sur lequel  f ne s'annule pas. L'équation est alors équivalente à yy' = -x c'est à dire à 2yy' = -2x. Par quadrature élémentaire, en intégrant de part et d'autre, on obtient y² = -x² + C, C constante arbitraire.

y² = -x² + C  ⇔ x² + y² = C

C = 0 est à rejeter. L'équation possède des solutions non nulles si et seulement si C > 0 et y ≠ 0. Posons C = r². L'ensemble des solutions est donné par :

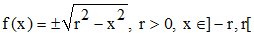
Les courbes intégrales sont des cercles de rayon r centrés en l'origine privés des points M(± r,0).

e2) Sous réserve des conditions y' ≠ 0 et x ≠ 0, l'équation peut s'écrire y"/y' = 2/x. Supposons ces conditions vérifiées et cherchons donc les solutions y = f(x) sur tout intervalle I ne contenant pas 0 et sur lequel  y' = f'(x) ne s'annule pas, ln désignant la fonction logarithme népérien, C une constante arbitraire et k = e^C > 0 :

y"/y' = 2/x ⇔ ln| y' | = 2ln| x | + C ⇔ ln| y' | = ln(x²)  + C  ⇔ ln| y' | = ln(x²) + ln(e^C)  ⇔ | y' | = kx²

On peut alors écrire y' = C₁x² en posant C₁ = ± k∈R*. Par suite y = f(x) = C₁x³/3 + C₂. Finalement, sur tout intervalle I ne contenant pas 0 :

f(x) = ax³ + b,  a∈R*, a∈R

Discussion :    

• Si la fonction dérivée y' s'annule sur un intervalle I, la solution est une fonction constante sur I. y" est également nulle : pas de contradiction. L'équation est triviale.

• Tout intervalle I contenant 0 peut s'écrire comme réunion I* de deux intervalles J* et K* privés de 0 sur lesquels f(x) = ax³ + b. Pour tout x de I*, f'(x) = 3ax², f''(x) = 6ax.  Les fonctions f, f' f''et sont continues en 0. On peut poser f(0) = b et f'(0) = f''(0) = 0 en prolongeant ainsi la solution générale précédente à R tout entier.

Dans le plan euclidien orienté, on considère la forme ω = xdy - ydx. Intégrer cette forme lorsque Γ est le cercle unité parcouru dans le sens direct puis lorsque Γ est le carré de côté 2, centré en O, de côtés parallèles aux axes parcouru également dans le sens direct.

Le cercle unité peut être paramétré par x = cost et y = sint, t parcourant l'intervalle [0,2π]. D'où :

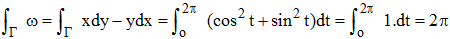
On constate que l'intégrale de ω est non nulle alors que Γ une courbe fermée : ω = xdy - ydx n'est donc pas une différentielle exacte.

Le long du carré, on a les représentations paramétriques :

• x = 1, y = t, t ∈ [-1,1], donc ω = dt          •      y = 1, x = -t, t ∈ [-1,1], donc ω = dt

• x = -1, y = -t, t ∈ [-1,1], donc ω = dt       •      y = -1, x = t, t ∈ [-1,1], donc ω = dt

Finalement :

On ne s'étonnera pas de trouver la "longueur du cercle" dans le 1er cas et le périmètre ("longueur") du carré dans le second : l'abscisse curviligne est ici ds = dt !

Lorsque la loi T est commutative et la relation ‹ réflexive et transitive, montrer que ‹ sera compatible avec T si et seulement si elle est régulière à gauche (ou à droite).

En se bornant au cas de la régularité à gauche :

• La condition est nécessaire (compatibilité) ⇒ (‹ est régulière à gauche) : supposons la relation ‹ compatible avec T et b ‹ b'; ‹ étant réflexive, a ‹ a pour tout a; d'où (a T b) ‹ (a T b') par compatibilité. La relation ‹ est donc régulière à gauche. On montrerait de même, en composant à droite par a que ‹ est régulière à droite.

• La condition est suffisante (‹ est régulière à gauche) ⇒ (compatibilité ) : supposons ‹ régulière à gauche et simultanément a ‹ a'  et b ‹ b' : on a alors (b' T a) ‹ (b' T a') et (a T b) ‹ (a T b'); vu la commutativité de T, on a d'une part a T b' = b' T a et d'autre part b' T a' = a' T b'. Le résultat (a T b) ‹ (a' T b') est alors acquis par transitivité de la relation ‹.

 Montrer que si A est un anneau intègre et unitaire, alors tout élément admettant un inverse à gauche (ou à droite), ou commutant avec cet inverse, est inversible.

Supposons x inversible à gauche dans A d'élément unité e. x est donc non nul. Utilisons la notation additive pour la loi de groupe et la notation multiplicative implicite pour la seconde loi. Il existe alors x' non nul dans A tel que x'x = e (x' inverse à gauche pour x).

On peut écrire x'x - e = 0 et par suite (x'x - e)x' = 0. Par associativité, on a :

(x'x)x' - x' = x'(xx' - e) = 0

Mais A est supposé intègre et x', inverse à gauche de x étant non nul, il suit que xx' - e est nul. donc xx' = e : x' est inverse à droite de x dans A. C'est donc l'inverse de x "tout court" (voir cet exercice).

 Montrer que tout anneau A unitaire intègre et de cardinal fini est un corps.

Notons 1_A l'élément unité de A et * sa seconde loi. Supposer que dans cet anneau, un élément a non nul ne soit pas inversible. L'application f_a de A dans A, définie par f_a(x) = a*x n'est alors pas surjective car f_a(x) = 1_A n'a pas lieu. A étant de cardinal fini, f_a n'est donc pas non plus injective. Il existe donc dans A deux éléments distincts a' et a" tels que a*a' = a*a". On en déduit que a est un diviseur de zéro. Conclure.

  Prouver qu'il existe un unique triplet de nombres premiers en progression arithmétique de raison 10.

On sait que tout entier naturel premier, autre que 2 et 3, est de la forme 6n ± 1, n décrivant N*. Soit p le plus petit des nombres premiers de la progression cherchée, à savoir : p, p + 10, p + 20. si p est de la forme 6a - 1, on aura p + 10 = 6a + 9, non premier. Si p est de la forme 6a + 1, on aura p + 20 = 6a + 21, non premier. Donc p ne peut être que 2 ou 3. Mais p = 2 est à rejeter car p + 10 = 12. Reste p = 3 fournissant p + 10 = 13 et p + 20 = 23. Et on s'arrête là car p + 30 = 33, non premier. C'est bon !

  La fonction récursive d'Ackermann vérifie :

• A(0,n) = n+1 pour tout n ≥ 0;

• A(m,0) = A(m-1,1), m ≥ 1;

• A(m,n) = A(m-1,A(m,n-1)), m ≥ 1, n ≥ 1 (récurrence double).

Montrer : a)  A(1,n) = n + 2.   b)  A(2,n) = 2n + 3.  c)  A(3,n) = 2ⁿ⁺³ - 3.

a) si n = 0, A(1,0) = A(0,1) = 1 + 1 = 2. A(1, n) = A(0, A(1,n-1)) = A(1,n-1) + 1 : on est en présence d'une suite arithmétique de raison 1, de premier terme 2. Donc  A(1, n) = 2 + n × 1 = n + 2

b)  On procède par récurrence :

i/ initialisation : si n = 0, A(2,0) = A(1,1) = A(0,A(1,0)) = A(1,0) + 1
                                              = 2 + 1 = 3 = 2 × 0 + 3 = 2n + 3.
ii/ hérédité : supposons A(2,n) = 2n + 3. A(2,n+1) = A(1, A(2,n))
                                            = A(2,n) + 2 = 2n + 3 + 2 = 2(n + 1) + 3.  CQFD.

c) On procède encore par récurrence :

i/  initialisation : si n = 0, A(3,0) = A(2,1) = 5 = 2³ - 3 = 2ⁿ⁺³ - 3.
ii/ hérédité : supposons A(3,n) = 2ⁿ⁺³ - 3. A(3,n+1) = A(2,A(3,n) = 2A(3,n) + 3 = 2(2ⁿ⁺³ - 3) + 3
                                            = 2ⁿ⁺⁴ - 3 = 2^(n+1)+3 - 3.  CQFD

 ➔    Le lecteur curieux peut maintenant passer à  m = 4 :

• A(4,0) = 13 = 2^(2^2) - 3

• A(4,1) = 65533 = 2¹⁶ - 3 = 2^(2^(2^2)) - 3

• ...

• A(4,n) = 2^(2^(2^(2^(2.......^2)))) - 3, l'expression contenant n + 3 présences de 2...

  Prouver que l'ensemble des nombres irrationnels est dense dans R.

Notons I l'ensemble des irrationnels. Il nous faut montrer que tout intervalle ]a,b[ de R contient au moins un élément de I.

Il existe n∈N tel que 1/n < b - a = d. Il suffit de choisir un entier naturel n > 1/d.

• si a∈I, a + 1/n∈]a,b[ et a + 1/n∈I car la somme d'un nombre rationnel et d'un nombre irrationnel est irrationnelle (c'est bien évident : raisonnez par l'absurde).

• si a∉I, alors a + 1/n√2∈I puisque √2 est irrationnel. Or √2 > 1 et par conséquent a + 1/n√2 < a + 1/n. Donc a + 1/n√2∈]a,b[.

  Calculer au moyen de votre calculatrice, en une seule séquence (pas de mise en mémoire, pas de résultats partiels), le nombre :

La séquence à taper sur votre calculatrice est :

On termine par = ou EXE ou ENTER suivant la calculatrice utilisée.

Penser que diviser par un produit A × B c'est diviser successivement A puis encore par B :

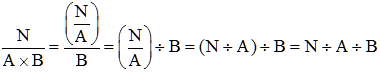
 ! N'ajoutez pas de ( ) sans précaution : on a pu enlever celles de N ÷ A car elles sont en début de calcul.
et on respecte l'ordre des opérations.

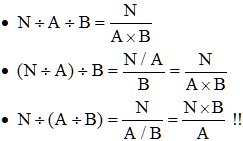
Exemple :   

• (12 ÷ 3) ÷ 4 = 4 ÷ 4 = 1

• Pas de (), on calcule dans l'ordre d'écriture12 ÷ 3 ÷ 4 = 4 ÷ 4 = 1

• 12 ÷ (3 ÷ 4) = 12 ÷ 0,75 = 16

  On considère la courbe (Γ) d'équation :  x = 2t³ + 3t² , y = 3t⁴ + 4t³. Montrer que cette courbe admet 2 points de rebroussement et un point double que l'on précisera.

1°/  Points stationnaires :

La tangente en chaque point est théoriquement dirigé par T₁(6t² + 6t, 12t³ + 12t²) mais ce vecteur est nul en t = 0 et t = - 1. Conformément à la théorie, on peut s'attendre dans ces deux cas à un rebroussement ou une inflexion.

Le vecteur dérivée seconde est T₂(12t + 6, 36t² + 24t). Non nul en t = 0 et t = - 1. Ce vecteur dirigera les tangentes aux points correspondants, soit en l'origine O(0,0) et en A(1,-1) respectivement.

• En t = 0, la courbe passe par l'origine et nous avons T₂(6,0). Considérons alors T₃(12, 72t + 24) = T₃(12, 24). T₂ et T₃ sont linéairement indépendants : (T₂, T₃) est une base du plan; nous sommes dans la configuration théorique p pair, q impair : la courbe passe par un rebroussement de 1ère espèce. La tangente de rebroussement est l'axe (Ox) des abscisses.

• En t = -1, la courbe passe par (1,-1) et nous avons T₂(- 6,12) et T₃(12, - 48). (T₂, T₃) est là encore une base du plan. La courbe admet un second rebroussement de 1ère espèce. La tangente de rebroussement a pour coefficient directeur y'/x' = 2t = -2. Son équation est donc y = -2x + 1 (en vert ci-dessous).

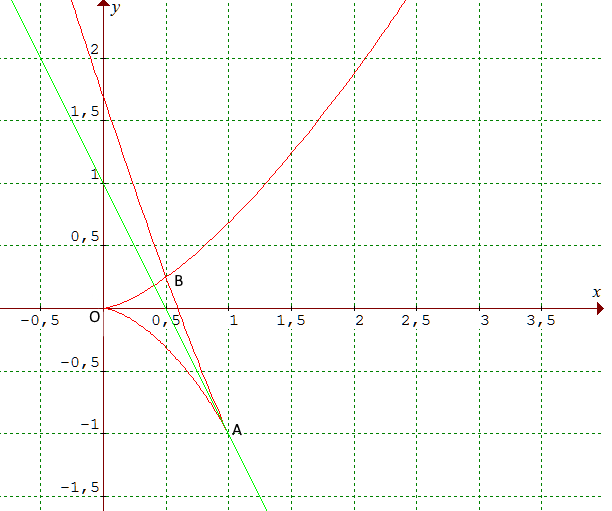
2°/  Point double :

La courbe semble admettre un point double de coordonnées (1/2,1/4). Vérifions cela. Il s'agit de résoudre le système :

2u³ + 3u² = 2v³ + 3v²
3u⁴ + 4u³ = 3v⁴ + 4v³
u ≠ v

On utilise u³ - v³ = (u - v)(u² + uv + v²) et u⁴ - v⁴ = (u - v)(u³ + uv² + u²v + v³). On simplifie par u - v. On remarque que u³ + uv² + u²v + v³ n'est autre que (u + v)(u² + v²). En posant S = u + v et P = uv, on a u² + v² = S² - 4P et finalement :

S(S² + 3S + 2) = 0
2S² + 3S = 2P

De la 1ère équation, on déduit S = 0 ou S = - 1 ou S = -2.

• S = 0, P = 0 : v = - u, uv = 0, donc u = v = 0 : à rejeter.

• S = - 2, P = 1 : u + v = -2, v = 1/u conduit à u = - 1, donc v = -1, à rejeter.

 ➔   On remarquera que les deux points qui viennent d'être rejetés sont les points de rebroussement déjà trouvés. Cela est bien normal : u = -v correspond au point origine que l'on peut atteindre par des valeurs supérieures ou inférieures de t, tout comme le point (1,-1) lorsque t tend vers -1 : ce sont en quelque sorte des faux points doubles.

• S = - 1, P = -1/2 : u + v = -1, uv = -1/2 conduit à u = (-1 + √3)/2, v = (-1 - √3)/2 ≠ u. Donc un point double. En reportant dans l'équation le point B de coordonnées (1/2,1/4) est confirmé.

La fonction à intégrer est paire. On intègrera de 0 à + ∞ et on multipliera le résultat par 2. En posant x = 2tan φ, on a cos²φ dx = 2dφ. Une petite manip élémentaire conduit à :

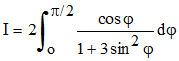
On se ramène à l'intégration d'une fraction rationnelle en posant maintenant t = sin φ :

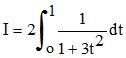
On pose enfin u = t√3 :

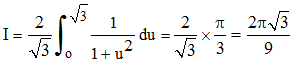
Maxf = ½. I ≅ 1,2092. On peut rapidement vérifier graphiquement l'ordre de grandeur de I par approximation des aires bleutées
afin de conforter le résultat théorique (1 unité d'aire 1/4).  » quadrature...

  Calculer l'aire de la surface engendrée par une arche de cycloïde tournant autour de l'axe des abscisses. » voir aussi autour de Oy.

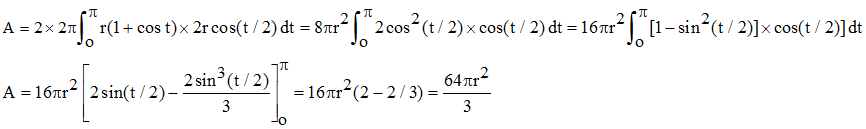
  Montrer que la suite des sommes partielles de la série de Riemann de terme général 1/n² est inférieure à 2 - 1/n.

Si S_n désigne la suite des sommes partielles de la série, on peut écrire :

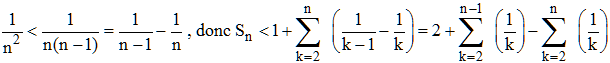
Finalement, S_n < 2 - 1/n. Ainsi, La suite (S_n), positive donc croissante et majorée par 2 est convergente : la série Σ1/n² converge et sa somme est inférieure (ou égale) à 2, limite de S_n. La somme est en fait égale à π²/6 :

Étude de ζ(2) = π²/6 :  ››››