ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

PTOLÉMÉE Claudius, grec, 90-168    » Zodiaque | Planisphères | Boussole & nord magnétique | Théorie des équants

Né à Ptolémaïs (Haute-Égypte), d'où son nom, cet illustre astronome et géographe vécut à Alexandrie. Son œuvre magistrale, la Composition Mathématique (vers l'an 150), treize livres, rebaptisé Megiste Syntaxis (le très grand traité), et l'Almageste par les astronomes et mathématiciens arabes (de al = le et megistos = très grand), est une vaste compilation des hypothèses et résultats obtenus à l'époque sur le mouvement des objets célestes que complète un traité de trigonométrie plane et sphérique basé sur la théorie des cordes. Dans son  impressionnant traité de Géographie (et cartographie, 8 livres, » réf.10), on lui doit les notions de latitude (du latin latus = large, latitudo = largeur) et de longitude (du latin longus = long, longitudo = longueur) d'un lieu terrestre. 

←  Portrait de Ptolémée issu du site spécialisé Iconographie du portrait de Ptolémée

Concernant ces coordonnées géographiques que sont la latitude et la longitude, la première ne pose pas de problème "local" mais la seconde nécessite un méridien origine. Ptolémée choisit les terres les plus occidentales alors connues en situant le méridien "0" sur une petite île de l'archipel espagnol des Canaries : El Hierro (en français, l'île de Fer) également appelée Isla del Meridiano en hommage à Ptolémée. Ce choix permet de couvrir d'Ouest en Est le monde connu en longitudes positives, le continent américain n'ayant été découvert qu'à la fin du 15è siècle (Christophe Colomb, 1492).

 i  On oublie souvent que le continent nord-américain fut découvert par les Vikings : ces célèbres guerriers navigateurs débarquent à Terre Neuve (Canada) peu après l'an 1000.

Les tables de Ptolémée mentionnent des milliers données mais contiennent de nombreuses erreurs. Une partie de ses tables furent corrigées plus ou moins bien par Al-Khwarizmi au 9è siècle. Mais en déplaçant le méridien origine vers l'Est sur la côte africaine il sema une grande confusion tout au long du Moyen-âge (» réf.11-12-13).

Le méridien origine fluctua au fil des ans et des latitudes. Certains astronomes arabes "occidentaux" (Maghreb, Andalousie) le placèrent au détroit de Gibraltar. D'autres au 11è siècle, à Tolède. Plus à l'Est en Égypte, le méridien d'Alexandrie fut aussi choisi. Les indiens, comme Brahmagupta et Bhaskara, utilisèrent Ujjain, une des 7 villes sacrées de l'Inde, berceau des astronomes indiens, en plaçant le méridien 0 sur la côte Est de la Chine (dans le monde arabe de l'époque, par déformations successives, Ujjain deviendra Arin). Tout cela, auquel s'ajoutent des mesures incertaines voire fausses, reste très confus.

Vers le 10è siècle, on utilisera des mesures plus précises basées sur les grands pôles culturels et scientifiques, Bagdad en particulier, définissant un méridien origine sans équivoque. La connaissance des latitudes et l'évaluation des distances sur un même parallèle permettront une cartographie relativement précise. La difficulté fut de représenter "à plat" une configuration sphérique. Al-Biruni, peu après l'an mille, apporta des méthodes de correction complexes usant de la projection stéréographique inventée par Hipparque de Nicée 150 ans avant J.-C. (» réf.12). Au 12è siècle, l'apparition de la boussole inventée par les géographes chinois au 9è siècle, changera la donne.

 i  Les premières boussoles étaient constituées d'une fine tige de magnétite, un oxyde de fer naturel se comportant comme un aimant. Placée sur une plaque légère de liège ou de bois dans un récipient d'eau, la tige s'oriente vers le nord magnétique de notre planète, direction proche du pôle géographique (du nord ou du sud selon la position de l'observateur), et engendrée par le noyau ferreux liquide de notre planète qui se comporte comme un gigantesque aimant. Le pôle nord magnétique n'est pas fixe; il évolue en fonction des aléas du noyau ferreux et a tendance actuellement à se déplacer vers la Sibérie, quittant le nord-ouest de l'archipel canadien du Nunavut en suivant une direction nord-nord-ouest. Pour un observateur donné, l'angle des directions des deux pôles (magnétique et géographique) s'appelle la déclinaison magnétique. Il dépend grandement de la latitude (» réf.15).

 ➔  On pourra lire en réf.11 un article de l'IGN (Institut Géographique National) résumant l'histoire des méridiens origine où l'on apprend que le méridien de l'île de Fer fut adopté par les cartographes français du 16è siècle et que Louis XIII l'officialisa en 1634. Il sera la référence jusqu'à la révolution française.

Système GMT, fuseaux horaires, temps UTC, ... sur la page consacrée à Pierre Méchain : »

L'Almageste, le système solaire selon Ptolémée, théorie des équants :

Inspiré des travaux d'Hipparque, l'Almageste décrit un géocentrisme harmonieux cher à Aristote : la Terre, immobile, est le centre du monde autour de laquelle tournent circulairement et à des vitesses uniformes, la Lune puis Mercure, Vénus, le Soleil, Mars (dont l'excentricité de l'orbite alerta Kepler 1500 ans plus tard au profit de l'héliocentrisme), Jupiter et Saturne et enfin, bien au-delà, les étoiles.

Les planètes tournent également sur elles-mêmes en se mouvant donc suivant une trajectoire épicycloïdale : au 16e siècle, l'héliocentrisme de Copernic, pressenti par Pythagore et Aristarque de Samos, conduisant à des orbites elliptiques découvertes par Kepler, complétera le modèle au début du 17è siècle après plus de 2000 ans d'ingénieuses recherches et donnant ainsi raison à Alphonse X, roi de Castille (1221-1284), passionné d'astronomie qui aurait dit, eu égard au système de Ptolémée (» At-Tusi) :

Si j'avais été chargé de constituer le système solaire, je l'aurais fait beaucoup plus simple...


 Le système solaire de Ptolémée

La théorie des équants :    

On savait, depuis Hipparque qu'un système céleste circulaire, concentrique et uniforme ne rend pas compte des observations astronomiques. Afin de pouvoir corriger les anomalies constatées tout en préservant le principe d'uniformité, Ptolémée envisagea un modèle épicycloïdal selon Hipparque augmenté d'une double excentricité :

Une planète P décrit uniformément un petit cercle, son épicycle, autour d'un centre O décrivant lui-même autour de la Terre T, un autre cercle (d) de centre D, dit déférent et de plus grand rayon R (orbite principale de la planète) de sorte que si T' est le symétrique de T par rapport à D, point équant, et (e) le cercle de centre T' de rayon R, alors le point E décrit (e) uniformément. Dans ces conditions, c'est le mouvement de O autour de D et de T qui n'est plus uniforme.

 

Ci-dessus : un timbre du Burundi illustrant le système géocentrique d'Eudoxe et de Ptolémée dans une représentation datant du 18è siècle (Bibliothèque Nationale). On y trouve, par ordre de distance croissante par rapport à la Terre : La Lune, Mercure, Vénus, le Soleil, Mars, Jupiter et Saturne.


Équants & animation : »

Ce système complexe permet d'expliquer, vues de la Terre, les variations de vitesse et d'éloignement des planètes. Mais le modèle excentré, plus simple, reste à l'époque très satisfaisant : Kepler le remplacera d'ailleurs par des trajectoires elliptiques de très faible excentricité, donc équivalentes à des orbites circulaires excentrées.

Mais quid d'Uranus, Neptune et Pluton ?     

La planète Uranus fut découverte (1781) par l'astronome anglais d'origine allemande William Herschel (1738-1822). Une nouvelle planète fut pressentie par l'astronome français Urbain Le Verrier (1811-1877) et l'anglais J. C. Adams (1819-1892) eu égard à des perturbations repérées dans les orbites des autres planètes (dont Uranus). Le Verrier se lança alors dans de puissants calculs qui durèrent deux ans et la planète, baptisée Neptune, fut effectivement découverte (observée) en 1846 par l'astronome allemand Johann Gottfried Galle là ou Le Verrier l'avait prédite. Ce fut là une preuve magnifique de la cohérence des théories de la gravitation et des perturbations des orbites planétaires. Élu à l'Académie des sciences la même année, la Sorbonne créa à son intention une chaire de mécanique céleste qu'il occupa jusqu'à sa mort. La découverte de Pluton est très récente : son existence fut décelée dans les mêmes conditions que Neptune par l'astronome américain Percival Lowell (1855-1916) et découverte par son assistant Clyde Tombaugh en 1930. Il n'y fait pas très chaud : -200° en moyenne...

En 2006, Pluton a été rétrogradée en tant que planète naine par l'Union Astronomique Internationale. Elle a ainsi perdu son rang de 9ème planète de notre système solaire.

» Ossian Bonnet , Nasir ad-Din at-Tusi

Rappelons que c'est à Galilée Copernic que l'on devra le retour (définitif) à un système héliocentrique que les  Pythagoriciens avait pressenti.

Ce n'est qu'au 16e siècle que l'héliocentrisme de Copernic, pressenti deux millénaires auparavant par les Pythagoriciens, simplifiera le modèle et conduira Kepler à découvrir, après quelques errances géocentriques, les orbites elliptiques des planètes autour du Soleil dans un mouvement finalement non uniforme.

Hipparque avait, trois siècles auparavant, observé et classé un grand nombre de constellations (groupement d'étoiles, du latin cum = avec, et stella = étoile). Ptolémée compléta ses observations et la nomenclature des constellations de l'hémisphère nord (boréal) : il en répertoria 48. Raison pour laquelle, les constellations de l'hémisphère nord portent des noms relevant de la mythologie grecque. Celles de l'hémisphère sud furent observés bien plus tard (18è siècle), en particulier au cap de Bonne Espérance, par l'astronome français l'abbé Nicolas Louis de La Caille.

 i  On doit à Ptolémée la dénomination actuelle des constellations (du latin cum = avec, ensemble et stella = étoile) proches du plan de l'écliptique : ± 8° de part et d'autre, dont l'observation remonte aux populations antiques de la Mésopotamie, Araméens en particulier. Leur ensemble constitue le Zodiaque (du grec zôdiakos diminutif de zôon = animal). Les représentations imaginatives qu'elles évoquent, au nombre de 12 (Bélier, Taureau, Gémeaux, ..., Poissons), permettent de situer rapidement un endroit du ciel étoilé. Elles font aussi l'objet d'une utilisation moins scientifique à l'intention d'une étonnamment importante partie des populations du globe : l'astrologie (» réf.7).


Zodiaque, constellations ou signes, une vidéo YouTube de Sébastien Beaucourt (» réf.7b)
 

Un très beau théorème de Ptolémée (Almageste, Livre I, ch.9) :

Théorème :  

Dans un quadrilatère convexe inscrit dans un cercle, le produit des diagonales est égal à la somme des produits des côtés opposés :

AC × BD = AB × DC + AD × BC

          » Preuve du Théorème de Ptolémée

 ➔   Ce résultat lui servit à établir des tables (longueurs de cordes de cercle en base 60) et des formules trigonométriques et permet en particulier d'établir la formule :

sin(a + b) = sin a × cos b + cos a × sin b

Preuve : lorsque [AC] est un diamètre du cercle, notons E le symétrique de D par rapport au centre, a = ^DAC et b = ^BAC.

Dans ces conditions : ^DEB = 180° - (a+b), les angles ^DAC, ^BAC et ^BED sont droits et on a : sin^DEB = sin[180° - (a+b)] = sin(a + b). Or, sin^DEB = DB/DE = DB/AC. On utilise alors la formule de Ptolémée au quadrilatère ABCD et on divise les deux membres de l'égalité par AC × AC :

DB/AC = AB/AC × DC/AC + AD/AC × BC/AC

Avec les notations de la figure, on obtient : sin(a + b) = cos b × sin a + sin d × cos c. Il 'agit bien de la formule recherchée car dans un triangle rectangle les angles aigus sont complémentaires : le sinus de l'un est le cosinus de l'autre.

Points cocycliques : »

∗∗∗
Quadrilatère d'aire maximale
 
Ptolémée et l'usage du système sexagésimal (base 60) :

Ptolémée calculait, en base 60, système de numération hérité des Babyloniens (dit sexagésimal, du latin sexaginta = soixante et sexagesimus = soixantième) au moyen de la mesure des cordes de cercles, ancêtres du sinus. Cet usage, appliqué en particulier aux calculs astronomiques, remonte à Hipparque. Contrairement à la base 10 qui ne possède que deux diviseurs propres (2 et 5), la base 60 en possède 10, à savoir : 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ce qui simplifie grandement les calculs, fractionnaires en particulier, à une époque où l'on manquait de moyens de calcul sophistiqués

La mesure du temps à l'origine du système de numération sexagésimal des Babyloniens : »

Ptolémée obtint cette remarquable approximation du rapport de la circonférence à son diamètre, fournissant l'approximation 3,1416 pour le nombre π, exacte à 0,0001 près :

3 + 8/60 + 30/602

Une valeur que l'on retrouve en Inde avec Aryabhata au 6ème siècle et, plus tôt et plus précise, en Chine avec Tsu Chung Chi au 5è siècle, proposant 3,14159266 (exacte à 10-8 près). Au 9è siècle, le célèbre algébriste et astronome persan Al-Khawarizmi adopte le calcul de Ptolémée qui sera curieusement ignoré par ses successeurs dont l'admiration pour ce dernier était pourtant sans conteste, et qui se contentèrent de 22/7 = 3 + 1/7, approximativement 3,1428, qu'Archimède utilisa en son temps (près de 4 siècles auparavant). Il fallut attendre Al-Kashi, au début du 15è siècle, qui obtiendra 14 décimales ! 

Le calcul de Ptolémée : »              Calculs de π dans ChronoMath  : »

L'usage de la base 60 nous est resté aujourd'hui tant dans la mesure des angles que dans celle du temps :

 »  Hypsiclès d'Alexandrie , Peletier du Mans

∗∗∗
Coïncidence des aiguilles d'une montre (exercice niveau 5ème et plus)

 Ptolémée et la trigonométrie des cordes :

La trigonométrie d'Hipparque et de Ptolémée est très proche de "la notre", laquelle remonte à Regiomontanus au 15è siècle : sur la figure ci-dessous, la corde de l'angle â est AB et C est le symétrique de A par rapport à (OB). Si nous notons d'une façon générale, cord(^x) la corde d'un angle ^x d'un cercle de rayon R, la corde interceptée par l'angle au centre de mesure 2â sera :

cord(2â) = 2AH = 2R × sin(â)

Lorsque R = 1, notre sinus actuel est donc la demi-corde de l'angle double

 ➔  Cette demi-corde fut introduite par l'indien Aryabhata au 5è siècle et adoptée par Al-Khwarizmi au 9è siècle. Le cosinus ne fut défini et utilisé que beaucoup plus tard par l'anglais Edmond Günter. On a :

cord(180° - â) = 2R × cos(â/2)

Prenons désormais R = 1, figure de droite, comme le firent ultérieurement les mathématiciens arabes comme Abu l'Wafa et Al-biruni; si â = ^AOA'; on a ^AOC = â/2 et BC = 2.

 

Connaissant la corde de l'angle â, on pouvait facilement calculer les cordes des angles correspondant à â/2 et 180° - â/2 en utilisant les simples propriétés des triangles semblables et des triangles rectangles. Par exemple, sur la figure de droite, la corde de â est AA', celle de â/2 est AC. 

Al Battani et les demi-cordes : »


Ptolémée, fragment de la fresque de Raphaël : École d'Athènes, chambre de la signature - Vatican
»  Web Gallery of Art : http://www.wga.hu/frames-e.html?/html/r/raphael

Cartes du ciel (planisphères céleste) :



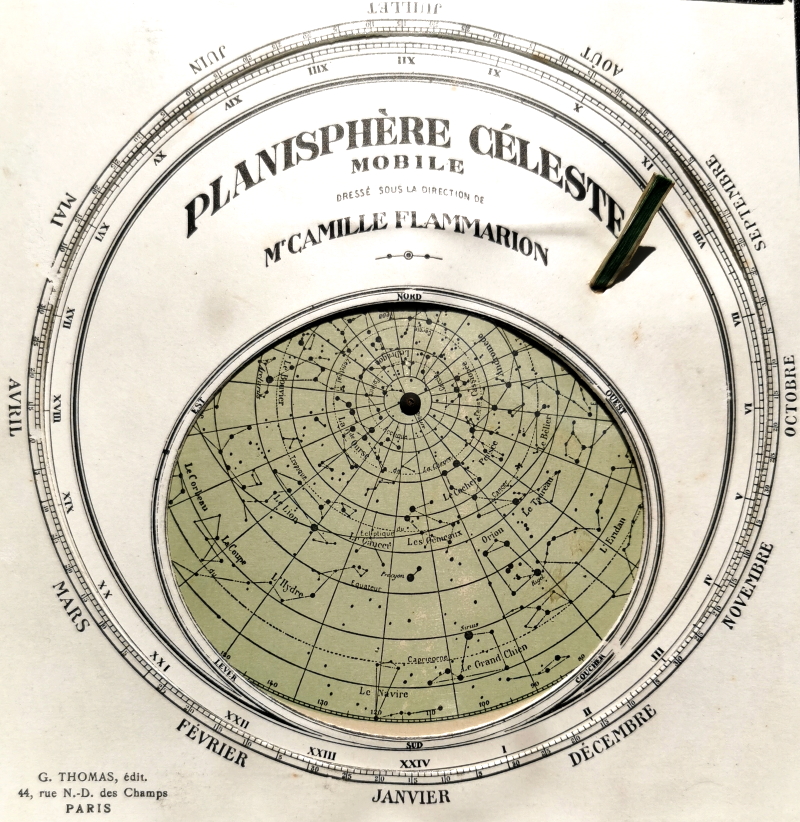
 Planisphère céleste nord mobile inclus dans l'Encyclopédie autodidactique Quillet, Tome 2 (1939)
Le centre de la sphère céleste est ici l'étoile polaire, étoile α de la Petite Ourse alias Polaris


Planisphère céleste interactif d'Olivier Esslinger. Accédez au site astronomes.com en cliquant sur l'image.
Vous devez vous imaginer allongé(e) sur le dos, admirant la voute céleste la tête au nord.
Entrer les latitude et longitude du lieu d'observation déterminera le centre du planisphère.
Une latitude négative vous fera passer dans l'hémisphère sud. Nombreux paramètres réglables dont une animation en continu.

 ➔  Pour en savoir plus :

  1. a) La théorie des sphères homocentriques, par M. Gabriel (univ. Liège) :
    http://adsabs.harvard.edu/full/1988C&T...104...87G
    b) Les sphères concentriques et les épicycles, par Yvon Georgelin, astronome (qui découvrit la structure spirale de notre galaxie) :
    http://astronomie.regards.free.fr/heliocentrisme/spheres.html

  2. La structure du Monde, du cosmos des mythologies au géocentrisme, par Vincent Deparis ENS Lyon) :
    https://planet-terre.ens-lyon.fr/ressource/cosmos-geocentrisme.xml

  3. Le Système du Monde, tome 1, La cosmologie hellénique, Ch. III, pages 111-129, par Pierre Duhem (1861-1916) sur Gallica :
    http://gallica.bnf.fr/ark:/12148/bpt6k97527176

  4. Histoire de l'astronomie moderne depuis l'École d'Alexandrie, par Jean Sylvain Bailly (1779) :
    https://books.google.fr/books?id=v8RZAAAAcAAJ&pg=PA242

  5. Astronomie & astrophysique, connaissances de base (observatoire de Lyon) :
    https://cral-perso.univ-lyon1.fr/labo/fc/cdroms/stages14-15/astrobase/ (nombreux documents pédagogiques)

  6. a) Le zodiaque par Pierre Causeret :
    http://clea-astro.eu/archives/cahiers-clairaut/CLEA_CahiersClairaut_135_05.pdf
    b) Zodiaque, constellations ou signes, une vidéo YouTube de Sébastien Beaucourt, auteur du site lecielenquestions.fr :
    https://www.youtube.com/watch?v=6oPKwvoX8T4
    c) #constellations : https://www.youtube.com/hashtag/constellations

  7. Planétarium (open source) : https://stellarium.org/

  8. Histoire d'algorithmes : du caillou à la puce, par une équipe d'enseignants (IREM, IUFM, CNRS)
    Éd. Belin - Collection Regards sur la science - 1993 -     Ch. 10

  9. La Composition Mathématique, traduction N. Halma (2 volumes, 1813-1816). Éditions A. Blanchard.
    » L'abbé Nicolas Halma (1755-1828) : géographe, historien et professeur de mathématiques.

    10.

  10. Géographie de Ptolémée :
    a) Reproduction d'une partie du manuscrit grec et cartes : https://books.google.fr/books?id=mUhNAAAAcAAJ
    b) Traduction par M. l'Abbé Halma, Paris, 1828 : https://books.google.fr/books?id=nCGnVT3CYRQC
    c) La géographie de Ptolémée (Wikipédia) : https://fr.wikipedia.org/wiki/Géographie_(Ptolémée)

  11. Histoire des différents méridiens origine (IGN) : https://geodesie.ign.fr/contenu/fichiers/Meridiens_greenwich_paris.pdf

  12. Histoire des sciences arabes, Tome 1 : Astronomie théorique et appliquée
    Livre contributif sous la direction de Roshdi Rashed. Un chapitre écrit par Edward S. Kennedy, historien des sciences arabes (1912-2009)
    est consacrée à la géographie et cartographie. Éditions du Seuil - Paris (1997). Lire en ligne : https://archive.org/details/RoshdiRasheded.EncyclopediaOfTheHistoryOfArabicScienceVol.3Routledge1996/Qisar-Roshdi-Rashed-...

  13. Geographical coordinates of localities in the al-Maghreb ans al-Andalus localities par Eric Mercier, univ. Nantes :
    a) https://www.raco.cat/index.php/Suhayl/article/download/377825/471181
    b) https://www.e-perimetron.org/Vol_15_2/Mercier.pdf

  14. La conquête des longitudes (une publication de l'APMEP) : https://www.apmep.fr/La-conquete-des-longitudes.

  15. Pôle nord magnétique :
    a) https://gisgeography.com/magnetic-north-vs-geographic-true-pole/#:~:text=What is the Magnetic North,of attraction enter the Earth.
    b) https://fr.wikipedia.org/wiki/Pôle_Nord_magnétique

Ménélaüs  Théon de Smyrne
© Serge Mehl - www.chronomath.com