
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


Philosophe, ami et disciple de Socrate, précepteur d'Aristote, Aristoclès, dit Platôn (le large) fut d'abord poète, dramaturge et politicien. Théodore de Cyrène lui enseigna les mathématiques. Il créa près d'Athènes, dans les jardins d'Akadêmos, l'Académie, une école de la philosophie et des sciences, au fronton de laquelle il fit inscrire :
|
Que nul n'entre ici s'il n'est géomètre |
Pour Platon, la géométrie (formes et raisonnements) est l'interface entre le monde matériel (l'Homme et les objets terrestres) et ce qu'il appelle les Idées d'essence divine : il s'appuie sur la raison afin de justifier l'existence du Bien et de la Vertu auxquels on ne peut accéder que par la dialectique (le dialogue, le raisonnement discursif) qui use des mathématiques (arithmétique et géométrie) élevant l'âme au-dessus des considérations matérielles, ainsi que de l'astronomie et l'harmonie (la musique).

Platon enseigne, entouré
de ses disciples (mosaïque, Pompéi)
Platon s'apparente au rationalisme cartésien. Il rejette les instruments de mesure et de construction à l'exception de la règle et du compas, car engendrant beauté et symétrie des formes, ces derniers peuvent expliquer l'harmonie du monde. Il est ainsi l'initiateur de la géométrie euclidienne dont les figures sont les objets « sur lesquelles les mathématiciens construisent leurs raisonnements, sans avoir dans l'esprit ces figures elles-mêmes mais les figures parfaites dont celles-ci sont les images visibles et que nul ne peut contempler autrement que par la pensée » (Platon, la République - VI, 510).
|
Problème de la duplication du carré : |
 Étant donné un carré, construire un carré d'aire double. Voici
comment, selon Platon,
Socrate
l'aurait proposé à un esclave (dialogue Le Ménon) afin de démontrer que
la science est en chacun de nous :
Étant donné un carré, construire un carré d'aire double. Voici
comment, selon Platon,
Socrate
l'aurait proposé à un esclave (dialogue Le Ménon) afin de démontrer que
la science est en chacun de nous :
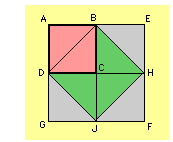
le carré donné est ABCD de côté 1 (à droite en rose). Le carré AEFG est de côté 2; le quadrilatère DBHJ, construit sur les milieux de côtés de ce carré, réalise la duplication du carré ABCD.
En vérité, l'esclave se trompa et pensa qu'il suffisait de doubler le côté du carré donné (ce qui quadruple l'aire initiale. Cette erreur est mise à profit pour faire apparaître le carré DBHJ en remarquant que la diagonale d'un carré partage celui-ci en deux triangles rectangles isocèles d'aire moitié. Ce principe philosophique initié par Socrate porte le nom de maïeutique, du grec maieutiké : art d'accoucher, ici : l'esprit, l'intelligence.
| Polyèdres de Platon : |
Dans son dialogue "Le Timée", du nom d'un mathématicien grec pythagoricien, Platon explique l'harmonie du Monde par l'existence des cinq (et cinq seulement) polyèdres réguliers convexes qui furent découverts par Théétète d'Athènes :

➔ Par convexe, on entend qu'il n'y a aucune présence de concavité : au sens latin, concave signifie qui possède un creux. Plus rigoureusement : un polyèdre est dit convexe s'il est entièrement situé dans un des demi-espaces défini par l'une quelconque de ses faces. Dans le cas contraire, on parle de polyèdre étoilé. C'est le cas des polyèdres de Poinsot, comme ci-dessous : le grand dodécaèdre étoilé de Poinsot (vous devez y "voir" des niches tétraédriques) :
La structure du dodécaèdre convexe formé de 12 pentagones réguliers, est liée au culte pythagoricien du pentagramme et au mystère des nombres irrationnels : le rapport d'une diagonale au côté n'est autre que le mystique, voire ésotérique, nombre d'or :
 Fibonacci et nombre d'or :
»
Fibonacci et nombre d'or :
»
dont l'inverse est Φ - 1 et le carré Φ + 1. Selon Iamblicus de Chalcis (Jamblique), Hippase de Métaponte, considéré comme le découvreur des nombres irrationnels, fut le premier mathématicien de l'antiquité à inscrire le dodécaèdre dans une sphère et il dut pour cela côtoyer la racine carrée de 5 et, par là, le célèbre et futur nombre Φ.
Étude des polyèdres réguliers : » Solides archimédiens (polyèdres semi-réguliers convexes) : »
|
Preuve par Legendre qu'il ne peut y avoir que cinq polyèdres réguliers (source Gallica) : |
