
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» racine n-ème & exposants fractionnaires | Exercices niveau collège | Notation scientifique. » Puissance & exposant selon d'Alembert , selon Newton. |
La notion de puissance en arithmétique et en algèbre s'immisce systématiquement dans tout contexte calculatoire où intervient une multiplication : calculs sur les nombres entiers, les nombres rationnels (fractions), les nombres réels ou complexes, calculs sur les fonctions, les polynômes, les matrices, ...
Cette page décrit de façon élémentaire, niveau collège et lycée (pour les nombres complexes), les différentes acceptions de la notion de puissance implicitement définie dans une structure algébrique, comme un anneau unitaire (A,+,×) ou un corps, permettant de donner un sens à des multiplications en chaîne dont les termes sont susceptibles d'être regroupés (associativité), voire déplacés (cas d'un anneau commutatif) sans nécessiter la présence de parenthèses. Pour cet aspect plus général, on se reportera à la page anneaux et corps.
L'ensemble A pourra en particulier être :
Z, R, ou C;
F : anneau des fonctions numériques munies de l'addition et de la multiplication;
G : anneau des fonctions numériques munies de l'addition et de la loi de composition des applications.
Mn(R) : anneau des matrices carrées réelles d'ordre n sur R;
...
|
Puissance n-ème d'un nombre réel ou complexe : |
On appelle puissance d'un nombre a le nombre obtenu par multiplications répétées de a par lui-même : si n est un entier naturel, on note an le produit de n éléments égaux à a, puissance n-ème de a :
an = a × a × a × ... × a
Dans cette écriture, on dit que n est placé en exposant et on lit a exposant n ou a puissance n. On dit aussi que a est élevé à la puissance n.
♦ Le cas n = 2 : plutôt que puissance 2-ème, on parle d'élévation au carré, allusion à l'aire a × a = a2 d'un carré de côté a, et on dit que a2 est le carré de a.
♦ Le cas n = 3 : plutôt que puissance 3-ème, on parle d'élévation au cube, allusion volume a × a × a = a3 d'un cube de côté a, et on dit que a3 est le carré de a.
5 élevé au carré donne 25; 4 élevé au cube donne 64. On dit plus succinctement "5 au carré", 4 "au cube".
26/32 = 64/32 = 2 ; (-5)3 × (-2)2 = -125 × 4 = -500.
102 = 100 , 103 = 1000 , 103 × 104 = 1000 × 10000 = 107 = 103 + 4.
10100 = 1 000 000 000 000 ... 000 (cent zéros) est un nombre énorme dépassant le nombre de particules élémentaires constituant notre univers, que l'on évalue entre 1080 et 1085, information qui, en fait, n'a que très peu d'intérêt car cela ne tient nullement compte de particules comme les neutrinos, les photons, la matière noire. Ce 10100 a un nom : c'est le googol ainsi appelé par le mathématicien américain Eward Kasner en 1938 et repris par les jeunes ingénieurs américains S. Brin et L. Page pour nommer leur société en 1996 : la célébrissime Google dont l'objectif (réussi) était de mettre en ligne, à la disposition du monde entier, un maximum d'informations de toute nature. On pourra consulter le lien Wikipédia sur l'histoire de cette société.
Dans L'associativité de la multiplication dispense de parenthèses. Par exemple :
a × a = a2 a3 = a × a × a = a × (a × a) = (a × a) × a = a2 × a = a × a2
a2
 a3 =
(a
×
a) × (a
× a
a3 =
(a
×
a) × (a
× a
 a)
= a
a)
= a
 a
a
 a
a
 a
a
 a =
a5.
a =
a5.
D'une façon, par regroupement des termes, on remarque que :
|
an × ap= an + p |
Exprimer n = 5 × 47 - 19 × 46 au moyen d'un carré : n = 46 × (5 × 4 - 19) = 46 = 43 + 3 = 43 × 43 = 642.
Deux cas particuliers :
an + 1 = an × a. Selon la règle ci-dessus, on est amené à convenir que a = a1.
D'autre part : an = an + 0 = an × 1 : on est amené à convenir que : a0 = 1.
|
a = a1 et ao = 1 |
On vérifiera facilement que :
|
(a × b)n = an × bn |
Formule de Moivre calculant zn, z complexe sous forme trigonométrique (niveau terminale) : »
|
Puissances d'exposant négatif (entier) d'un nombre réel ou complexe : |
Lorsque a n'est pas nul, si l'on considère le quotient de deux puissances entières positives de a, comme a5/a3 ou a3/a5, on constate par simplification que a5/a3 = a2 et a3/a5 = 1/a2. Ce qui induit une règle et une nouvelle notation :
|
an/ap = an - p et 1/an = a-n |
10-1 = 1/10 = 0,1 • 10-2 = 1/100 = 0,01 • 10-4 = 0,0001 , ...
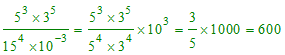
Donner la valeur décimale de x = 2
 10-3 + 2-3
sans utiliser une calculatrice ! Rép. :
2
10-3 + 2-3
sans utiliser une calculatrice ! Rép. :
2
 0,001 + 1/8 = 0,002 + 0,125 =
0,127
0,001 + 1/8 = 0,002 + 0,125 =
0,127
|
Puissance (entière) d'une puissance d'un nombre réel ou complexe : |
|
(an)p = anp |
Preuve : (an)p = an × an × ... an (p facteurs). Selon la propriété (a × b)n = an × bn, on déduit (an)p = an + n + ... + n = anp

|
Notation puissance d'une racine n-ème d'un nombre réel positif : |
Peut-on donner un sens à l'écriture a1/n, n entier non nul ? Selon la formule ci-dessus, nous aurions (a1/n)n = an/n = a1 = a. On convient alors d'écrire :
|
|
Autrement dit : r = a1/n ⇔ rn = a. En particulier :
|
|
Remarquer que le cas n = 1, racine 1-ème de a, n'est pas dénuée de sens : c'est a puisque r = a1/1 équivaut à r1 = r = a.
r = (ab)1/n ⇔ rn = ab = (a1/n)n × (b1/n)n = (a1/n × b1/n)n donc r = a1/n × b1/n. Autrement dit :
|
|
➔ Si a < 0, dans le cas n impair, on peut donner un sens à la racine n-ème de a, comme la racine cubique, par exemple. En effet, dans ce cas impair, comme ci-dessous pour n = 3, la fonction x → xn est impaire et on est en droit d'écrire :

Puissance fractionnaire p/q d'un nombre réel positif :
Les deux dernières définitions permettent de donner un sens à ap/q :
|
|
|
Notation scientifique d'un nombre réel : |
Lorsqu'un nombre est très petit ou très grand, il est d'usage dans les sciences de l'écrire au moyen des puissances de 10 positives, s'il est très grand, ou négatives s'il est très petit. Précisons en donnant deux exemples :
➔ Rappelons ici que multiplier par 10n un nombre décimal revient à décaler sa virgule de n rangs vers la droite ou vers la gauche suivant que n est positif ou négatif.
2 778 000 000 peut aussi s'écrire 2 778 × 106 mais ce n'est pas l'écriture dite scientifique de ce nombre. La règle est la suivante :
L'écriture scientifique d'un nombre est obtenue en l'écrivant sous la forme n,d × 10k où :
Une calculatrice donne généralement le résultat d'un calcul sous la forme scientifique si ce dernier est trop petit ou trop grand :
!
Niveau terminale : Le cas de la racine n-ème d'un
nombre complexe est beaucoup plus... complexe
!
La notation z1/n
pour un complexe n'a pas de sens :
Racines n-èmes d'un nombre complexe, racines n-èmes de l'unité : »
|
Puissance réelle d'un nombre a réel positif : |
On entre là dans le champ des fonctions exponentielles. Si x est un nombre réel et a > 0, parler de ax, c'est parler de la fonction exponentielle de base. Plutôt que a puissance x, On dira a exposant x. Un cas particulièrement important est la fonction exponentielle x→ex, réciproque de la fonction logarithme népérien. Si on donne un sens au nombre y = ax, alors en passant au logarithme népérien, on a : ln y = x × lna, c'est dire que :
|
ax est le nombre transcendant exlna |
Fonctions exponentielles, propriétés fonctionnelles et algébriques : »
|
Puissance complexe d'un nombre réel x > 0 : |
Soit x ∈R, x > 0 et z = a + ib un nombre complexe, a et b réels. Peut-on donner un sens à xz ?
On a formellement : xz = xa + ib = xa × xib. Or, e désigne la base des logarithmes népériens, depuis Euler, on a donné un sens à eit avec t réel : eit = cost + isint. Le logarithme népérien étant la fonction réciproque de x→ex, le nombre réel strictement positif x peut s'écrire elnx. On est alors en droit d'écrire xib = (elnx)ib = eiblnx et finalement :
|
xz = xa + ib = xa[cos(b × lnx) + isin(b × lnx)] : nombre complexe de module xa, dont un argument est b × lnx |
! La puissance complexe d'un nombre complexe n'a généralement pas de sens. Il ferait intervenir un logarithme complexe dont la détermination n'est pas unique :
Fonction exponentielle et logarithme complexe : »