ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Applications de la propriété de Thalès       » Point et nombres constructibles, construction d'un produit, d'une moyenne proportionnelle (moy. géométrique)            Partage d'un segment dans un rapport donné | Hauteur des pyramides d'Égypte

♦ Par point constructible du plan, on entend "à la règle et au compas". Cela sous-entend que l'on s'est donnés préalablement certains éléments : point(s), droite(s), cercle(s) rendant possible cette "construction à la règle et au compas".

Par exemple :

Le milieu d'un segment [AB], où A et B sont deux points donnés du plan, est constructible : il est l'intersection de [AB] avec la droite passant par les deux points d'intersection des cercles de centre A passant par B et de centre B passant par A. Cette droite n'est autre que la médiatrice de [AB], constructible à la règle et au compas comme on vient de le dire...

»  Euclide , Platon , Mohr , Mascheroni , Napoléon , Wantzel

♦ Nombres constructibles :

Étant donné un point A du plan et une unité de mesure, soit B un point du plan défini par une mesure m = AB. On dit que m est un nombre constructible si le point B est constructible.

• Dans un repère du plan, l'abscisse ou l'ordonnée d'un point constructible, est constructible.
• Une droite est constructible si deux de ses points le sont.

• Un cercle est constructible si son centre (point) est constructible et si son rayon (nombre) l'est aussi.

♦ Étant donnés a et b constructibles, on construira leur produit ab en appliquant la propriété de Thalès à la proportion :

     

et si b = a, on obtient la construction du carré de a.

♦  Étant donné y constructible, on construira une fraction a/b de y en écrivant que si x = a/b × y, alors

Les nombres constructibles sont dénombrables : »

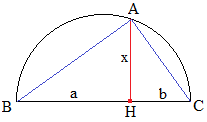
♦  Étant donnés a et b constructibles, on pourra aussi facilement construire une moyenne géométrique x, c'est à dire vérifiant x² = ab équivalent à x/a = b/x (moyenne proportionnelle) sachant que dans un triangle rectangle ABC de hauteur AH, on a AH² = HB × HC. () :

      » Pythagore | exercice TD 3è/2nde

• On construit un segment [BC] contenant H tel que BC = BH + HC = a + b;

• On trace le demi-cercle supérieur de diamètre BC;

• La droite perpendiculaire à [BC] passant par H coupe le demi-cercle en A.

On a x = AH car le triangle ABC est rectangle en A et si b = 1, on a alors construit la racine carrée de a.

Le corps des nombres constructibles, noté ici C, est stable par passage à la racine carrée, c'est à dire :

Si x appartient à C, alors la racine carrée de x est aussi élément de C.

On dit que C est un corps pythagoricien (appellation en hommage à Pythagore qui "découvrit" les nombres irrationnels. A noter que C est aussi le plus petit corps pythagoricien inclus dans R.

La propriété de Thalès permet de construire aisément, à la règle et au compas (construction au sens d'Euclide) le point M d'un segment [AB] tel que AM/AB = 1/n ou bien tel que AM/AB = a/b :

Ci-dessus, on a choisi de placer M tel que AM/AB = 1/5 et N tel que AN/AB = 3/5. Pour ce faire :

• Tracer une droite quelconque passant par A. On peut, sans restreindre la généralité, choisir la perpendiculaire à [AB] passant par A;

• Par symétries centrales successives, reporter 5 longueurs égales;
• Par le dernier point obtenu, ici appelé E, tracer (BE);
• La parallèle à (BE) passant par le premier point C fournit M tel que AM/AB = 1/5;
• La parallèle à (BE) passant par le troisième point D fournit M tel que AN/AB = 3/5.

Configuration croisée et construction des points M de (AB) tels que MA/MB = a/b : »

On en déduira la hauteur SA = DE x OA/OE. Donc, pour votre prochain voyage au pays des pharaons, à vos calculettes...