ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Pentagramme
#2
(ou pentacle, symbole de ralliement de
la secte
Pythagoricienne) niveau 1ère S
» pentagramme #1 (niveau 6ème) | Construction d'un angle de mesure 36° (π/5) |
On considère un pentagone régulier ABCDE. On trace ses diagonales. On obtient le pentagone JFGHI. Il est régulier, c'est bien évident et on l'admet.
On sait, par construction, que dans un pentagone régulier, le rapport de la diagonale au côté est égal au nombre d'or. On pourra admettre ce résultat.
➔ Le pentagone régulier croisé (dit étoilé) ACEBD, « étoile » à 5 branches, est le pentagramme cher à Pythagore.
Ta mission : calculer le rapport exact entre les aires de ces pentagones.
Si tu sèches après avoir bien cherché : ››››
» pentagramme niveau 6ème , pentagone et décagone régulier , pentagone régulier selon Dürer
| Solution : |
Des considérations élémentaires permettent d'établir les résultats codés sur la figure ci-dessous.
Posons c = AF et considérons le triangle isocèle FBG. On a :
D'où : AG/FG = (c + 2c × cos72)/ (2c × cos72).
Soit :
On sait que (» étude du décagone régulier) :
où Φ désigne le célèbre nombre d'or vérifiant Φ - 1 = 1/Φ. Par suite, une belle formule :
AG/FG = 1 + Φ = Φ2
et le rapport des aires est donc finalement :
Prolongement : construction d'un angle de mesure π/5 :
On remarque que (√5 +1)2 = 6 + 2√5 = 2(3 + √5). Un angle de 72° correspond, en radians, à 2π/5. On connait la formule cos2x = 2cos2x - 1, ce qui permet d'établir facilement :
➔ Notons au passage que le sinus de cet angle remarquable est alors (vérifiez-le) :
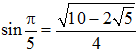
L'algorithme ci-dessous conduit à la construction de cos(π/5) et d'un angle
de mesure π/5
Dans un repère orthonormé (O,x,y) du plan, on trace le cercle trigonométrique (centre O, rayon 1).
Placer A(1,0) et B(0,2) // AB = √5;
Le cercle de centre A passant par B coupe [OA) en C. // OC = OA + AC = 1 + √5;
Construire J milieu de [OC] puis M milieu de de [OJ] // OJ = JC = (1 + √5)/2, OM = cos(π/5);
La perpendiculaire en M à [OA) coupe le cercle trigonométrique en D et E // ^AOE = ^AOD = π/5.
En conclusion ED est la mesure du côté du pentagone régulier inscrit dans le cercle unité. EA est celui du décagone régulier.
Étude du pentagone et du décagone régulier : »