
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
 Située
entre le Tigre et l'Euphrate dans l'ancienne Mésopotamie (du grec meso
= entre et potamos = fleuve),
au sein du pays Sumer où l'écriture vit le jour au 4è siècle avant Jesus-Christ, Babylone est aujourd'hui à l'état de ruine. Son nom originel Bab
Elli signifie la porte de
Dieu, c'est la Babel
de la Bible.
Située
entre le Tigre et l'Euphrate dans l'ancienne Mésopotamie (du grec meso
= entre et potamos = fleuve),
au sein du pays Sumer où l'écriture vit le jour au 4è siècle avant Jesus-Christ, Babylone est aujourd'hui à l'état de ruine. Son nom originel Bab
Elli signifie la porte de
Dieu, c'est la Babel
de la Bible.
Bâtie il y a près de 2500 ans à 160 km de Bagdad, capitale de l'actuel Iraq, la nouvelle cité fut la consécration de la civilisation chaldéenne (la Chaldée, à laquelle fait allusion la Bible, désigne la région sud de la Mésopotamie ou se rejoignent le Tigre et l'Euphrate).
 La ville doit sa puissance aux conquêtes de
Nabuchodonosor Ier (vers -1137) puis son éclat, bien plus tard
après des périodes de troubles et d'asservissement par
les Assyriens, sous le règne de Nabuchodonosor II (vers - 600).
Les jardins suspendus, s'ils existèrent
(selon
Hérodote),
dateraient de cette époque et sont classés parmi les
sept merveilles du Monde avec : mot clé mésopotamiens
La ville doit sa puissance aux conquêtes de
Nabuchodonosor Ier (vers -1137) puis son éclat, bien plus tard
après des périodes de troubles et d'asservissement par
les Assyriens, sous le règne de Nabuchodonosor II (vers - 600).
Les jardins suspendus, s'ils existèrent
(selon
Hérodote),
dateraient de cette époque et sont classés parmi les
sept merveilles du Monde avec : mot clé mésopotamiens
On estime que l'écriture a vu le jour en Mésopotamie il y a 5500 ans. Les savoirs des Chaldéens et des Babyloniens nous sont connus grâce aux nombreuses tablettes d'argile gravées en écriture cunéiforme, en forme de "coins" au moyen d'une tige de roseau taillée en biseau (appelée calame). Elles relatent leur vie sociale, commerciale, religieuse, culturelle et scientifique.
L'écriture cunéiforme des Babyloniens est alphabétique et se lit de gauche à droite. Elle fut déchiffrée relativement facilement au 19è siècle (si on la compare aux hiéroglyphes) par un linguiste allemand de Göttingen.
Avec les Sumériens, les Babyloniens furent, près de 2000 ans av. J.-C., de brillants astronomes et de grands calculateurs. Leurs tablettes montrent de savants calculs entiers, fractionnaires et irrationnels dont les objectifs premiers fut les calculs financiers et d'arpentage (mesure des terres agricoles). La Mésopotamie apparaît ainsi comme le berceau des mathématiques pures et appliquées.
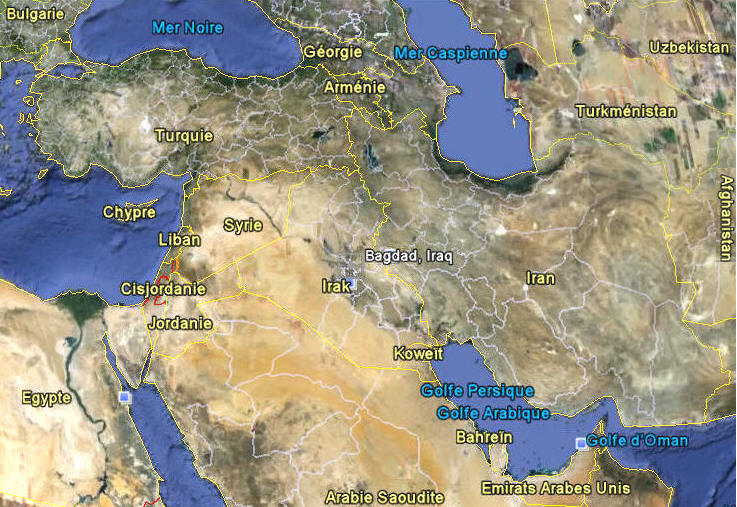
» Source
Google Earth :
http://maps.google.fr/maps?ll=33.315701,44.392197&z=4&t=h&hl=fr
|
Le système de numération sexagésimal, calendrier et mesure du temps : |
Héritée des Sumériens, l'année babylonienne commençait à l'équinoxe de printemps (21 mars) et comptait 360 jours basée sur 12 mois "lunaires" estimés à 30 jours, les lunaisons, intervalles de temps entre pleine Lune et nouvelle Lune (estimées de nos jours à 29 j 12 h 44 min). On croyait alors à la Terre fixe, le Soleil tournant circulairement autour d'elle. Parfaitement conscients que cette révolution solaire était d'environ 365 jours, une correction était apportée périodiquement afin de faire coïncider l'année lunaire et l'année solaire (on parle de calendrier luni-solaire).
Clavius et le calendrier grégorien : » » Méton , Hipparque , Ptolémée , Galilée , Copernic , Kepler
Tout particulièrement à cette époque (exempte de calculatrice...), 360 possède un avantage non négligeable : il favorise les calculs astronomiques car il possède un grand nombre de diviseurs, à savoir 24 :
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
Nombre de diviseurs d'un entier naturel : »
Les Babyloniens décidèrent d'un système de numération positionnel de base 60, système appelé aujourd'hui sexagésimal, du latin sexaginta = soixante et sexagesimus = soixantième). Adeptes de puissants calculs fractionnaires, le choix d'une telle base peut s'expliquer du fait qu'elle permet d'exprimer simplement de nombreuses fractions usuelles (décomposition en fractions unitaires, aussi appelées quantièmes), dont les anciens firent grand usage, grâce à ses 12 diviseurs : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Par exemple, à l'université de Yale (USA), la tablette Plimpton 232 montre un calcul de √2 à 10-7 près exprimé dans cette base. Une autre tablette, Plimpton 322 (université Columbia de New York, USA) exprime le théorème de Pythagore.
La mesure du temps :
 Le partage d'un
jours en 24 heures (en fait 12 "kaspars" , 1 kaspar = 2
heures) est aussi, avec les premiers cadrans solaires, un
héritage chaldéen : les égyptiens, admiratifs de la voûte étoilée
nocturne, partagèrent le ciel en 36 fuseaux (noter que 36 × 10°
= 360°, d'où l'appellation décan de
l'astrologie), chacun dédié à une divinité. L'observation du passage au
zénith
des diverses constellations permettait la mesure le temps.
Le partage d'un
jours en 24 heures (en fait 12 "kaspars" , 1 kaspar = 2
heures) est aussi, avec les premiers cadrans solaires, un
héritage chaldéen : les égyptiens, admiratifs de la voûte étoilée
nocturne, partagèrent le ciel en 36 fuseaux (noter que 36 × 10°
= 360°, d'où l'appellation décan de
l'astrologie), chacun dédié à une divinité. L'observation du passage au
zénith
des diverses constellations permettait la mesure le temps.
Plus tard, la subdivision du ciel est ramené à 24 et les grecs adopteront ce partage du jour (24 heures) dont nous avons hérité de par l'influence des célèbres astronomes Hipparque et Ptolémée avec le partage de la circonférence en 360 degrés, adapté à l'antique système de numération sexagésimale (base 60). A noter que l'année babylonienne comptait 360 jours : multiple de 60.
On l'apprend à l'école, l'heure est ainsi partagée en 60 minutes et la minute en 60 secondes.
Sachant aujourd'hui que la Terre tourne sur elle-même en une journée, chaque point de la Terre, à une latitude donnée, décrit donc un cercle en 24 heures, c'est à dire un arc de cercle de 360/24 = 15° par heure, ce qui détermine nos 24 fuseaux horaires actuels.
Une minute d'arc = 1/60ème de degré, 1 seconde d'arc = 1/60ème de minute (soit 1/3600ème de degré ou encore 1/602).
Le lien étroit entre la mesure du temps et la rotation de la Terre (qui dit rotation, dit angle...) permet de comprendre le pourquoi des mêmes dénominations pour les sous-unités d'heure et de degré.
Le temps GMT, Greenwich Mean Time : » » Clavius et les calendriers julien et grégorien
La multiplication babylonienne :
Les Babyloniens utilisaient des tables de carrés et non pas des tables de multiplication à la manière de Pythagore. Ils utilisaient en effet une formule basée sur les identités remarquables classiques apprises aux collèges :
(a + b)2 = a2 + 2ab + b2 et (a - b)2 = a2 - 2ab + b2, d'où, par différence :
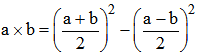
Par exemple : 13 × 17 = (30/2)2 - (4/2)2 = 152 - 4 = 221.
Calcul de la circonférence du cercle :
On a récemment trouvé (1936) à Suse (Mésopotamie), une tablette cunéiforme montrant que les Babyloniens utilisèrent pour le calcul de la circonférence du cercle, outre le triple du diamètre (soit la valeur très approximative π = 3), le nombre 3 + 1/8 = 3,125.
» Ahmes Méthode des périmètres pour le calcul de π : »
» Il semble que ce soit en Mésopotamie, 4000 ans avant Jésus-Christ, que la roue fut "inventée" : c'est en effet vers cette époque, à Uruk, que sont rencontrées, sur des tablettes d'argile, les plus anciennes représentations de chars à deux roues tirés par des chevaux.
Suivant le contexte, le symbole
![]() désignait
l'unité (1) ou la base (60). 10 était
représenté par
désignait
l'unité (1) ou la base (60). 10 était
représenté par
![]() .
Les Babyloniens sont ainsi à l'origine de nos systèmes
décimal et sexagésimal, ce dernier est utilisé
depuis pour mesurer le temps et les angles.
.
Les Babyloniens sont ainsi à l'origine de nos systèmes
décimal et sexagésimal, ce dernier est utilisé
depuis pour mesurer le temps et les angles.
Extraction d'une racine carrée à la manière des Babyloniens : » Numération babylonienne : »
➔ Pour en savoir plus :
Le pays Sumer (Wikipédia) : https://fr.wikipedia.org/wiki/Sumer
Entre le Tigre et l'Euphrate, il y a quelques millénaires (blog Emereka) : http://emereka.over-blog.com/archive/2020-06/
Écriture cunéiforme, sur le site de la Bibliothèque nationale de France : http://classes.bnf.fr/dossiecr/in-cunei.htm
Calendriers de la Mésopotamie, sur Wikipédia : https://fr.wikipedia.org/wiki/Calendrier_mésopotamien