Perspective & Géométrie Projective

Très abstraite en dehors de quelques généralités et principes de base exposés ci-dessous, la géométrie projective est relativement difficile à appréhender et requiert, avant de s'y plonger, une bonne connaissance en géométrie élémentaire et une bonne maîtrise de l'espace tridimensionnel, dans le cycle observation-représentation-interprétation, qu'un adolescent ne peut acquérir ou posséder au lycée. C'est pourquoi, en dehors de quelques de ses outils, comme l'usage des coordonnées barycentriques, de la division harmonique et des notions de polaires restreintes à l'espace affine, elle n'a pas été enseignée dans l'enseignement secondaire.

La déferlante axiomatique de la période des mathématiques modernes a éliminé des programmes de mathématiques ces éléments fondamentaux de la géométrie projective, dont les rudiments dans les programmes étaient complétés par ceux de la géométrie descriptive de Monge.

Le retour à la géométrie pure (1985) s'est limité à la géométrie euclidienne et aux transformations affines répondant mieux à l'objectif "faire des mathématiques pour raisonner" en s'affranchissant des excès de la géométrie du triangle à laquelle était soumis l'enseignement des mathématiques depuis la seconde moitié du 19è siècle. Seconde moitié où les premiers besoins technologiques de l'ingénieur (fabrication, construction mécanique, architecture) se sont appuyés sur les géométries projective et descriptive. Leur usage dans ces applications industrielles est aujourd'hui suranné compte tenu de la complexité des objets et du manque de précision obtenue.

Il est fait ci-dessous une approche élémentaire dépourvue de tout développement ou résultat dans le plan ou l'espace projectif. Le lecteur intéressé trouvera au long de cette page et in fine les références nécessaires à une étude approfondie.

Avec sa théorie des transversales, Pappus d'Alexandrie fut, au 3è siècle, le premier à exprimer une vision projective en géométrie, point de vue (sans jeu de mots...), repris par Desargues puis Pascal, mais principalement développée au 19è siècle par Chasles et son élève Poncelet en France, Möbius, Plücker, von Staudt en Allemagne, Véronèse et Cremona en Italie.

Qualifiée de supérieure jusque dans les années 1930, cette géométrie s'opposait à la géométrie euclidienne dite élémentaire et à la géométrie analytique (celle de Descartes faisant usage des coordonnées). On parlait aussi de géométrie synthétique, de géométrie de position ou de situation.

La géométrie projective repose sur la projection centrale (ou perspective, notion développée ci-après) et étudient les figures au point de vue de leurs positions respectives et des propriétés invariantes qui les lient dans une transformation géométrique, homographique tout particulièrement.

Cette géométrie permet d'établir de façon élégante des résultats de la géométrie élémentaire en évitant les discussions sur les cas particuliers de figures liées à l'existence de points d'intersection.

Désireuse de théoriser et compléter avec rigueur la géométrie euclidienne, mettant à mal le 5ème postulat et usant elle-même d'un principe assez flou (principe de continuité), elle n'a pas complètement convaincu malgré les efforts de Klein et son programme d'Erlangen visant à l'intégration des diverses géométries (euclidiennes et non euclidiennes) dans une même théorie unificatrice basée sur les groupes de transformation. Les travaux de Klein marqueront d'ailleurs un point final à son extension au profit de la géométrie algébrique.

La perspective centrale de la géométrie projective (du latin perspicere = voir à travers qui a aussi donné perspicace, qui comprend vite), également appelée

projection centrale ou projection conique est relative à une droite ou un plan : une telle projection, de centre O (œil de l'observateur), sur un plan (P) est l'application qui à tout point M d'une figure de l'espace associe le point M' de (P) tel que O, M et M' soient alignés.

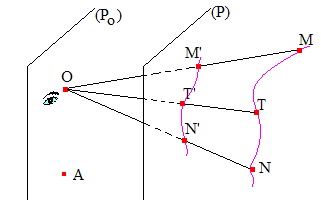
Les points de (P) sont invariants. Cette perspective ne fournit pas d'image pour un point A du plan (P_o)//(P) contenant O. Si (P_o) est "pratiquement" parallèle à (P), le point image A' existe mais est "très loin" sur P : la position limite (P_o)//(P) correspond à une image A' rejetée à l'infini.

exemple plan

On peut concevoir une géométrie projective construite dans un monde surréaliste (S) à courbure constante, comme le fit Klein pour caractériser les géométries non euclidiennes. Auquel cas, la projection centrale ne se ferait pas sur une droite ou un plan mais sur un sous-espace de (S), variété algébrique de (S).

Le point M' est la perspective de M sur le plan (P). Suivant la position de l'observateur et du plan de projection, la perspective d'un objet peut différer : un cercle est généralement vu comme une ellipse mais il peut être vu comme un cercle; un carré peut devenir rectangle ou trapèze !

Bien que conservant l'alignement et l'intersection, la projection centrale ne conserve en général pas les milieux et par suite ne conserve ni le parallélisme ni les rapports de distance. Ne conservant pas les milieux (et le barycentre d'un système fini de points), la projection centrale n'est donc pas une application affine. C'est une transformation homographique non affine.

Une illustration d'une perspective centrale dont le centre est ici l'auréole du Christ.
Les noces de Cana, P. Véronèse, 1563 (Musée du Louvre), Source illustration : Wikipedia

En géométrie élémentaire (affine), on parle parfois de coordonnées homogènes d'un point M : il s'agit en fait des coordonnées barycentriques lorsqu'on ne les assujettit pas à la condition x + y + z = 1 (normalisation) mais seulement à x + y + z

0, sinon, le barycentre (le point M) apparaît comme "rejeté à l'infini".

En effet, dans le plan par exemple, O désignant un point quelconque, la relation barycentrique

et si x + y +z tend vers 0, OM devient infini, d'où cette interprétation d'infinitude. Ces coordonnées barycentriques homogènes sont à distinguer des coordonnées homogènes (dites aussi coordonnées projectives) de la géométrie projective. L'exposé ci-dessous s'inspire du cours de Marcel Condamine, classe de Terminale C-E (1971).

On considère un plan affine (E₂) et son espace vectoriel associé (

₂) de dimension 2. Pour fixer les idées, (E₂) est le plan euclidien usuel (P) et

₂ l'ensemble des vecteurs de ce plan (plan vectoriel).

On note (P*) le plan (P) privé de l'origine O et (

₂*) le plan vectoriel privé du vecteur nul, identifié aux directions de (P). Soit (O,Ox,Ot) un repère (cartésien) de (P), (d) la droite d'équation t = 1.

On suppose ici M(x,t), t

0, un point de (P) dans ce repère. Le vecteur v = OM de

₂ définit une direction du plan et, comme l'arbre qui cache la forêt, tout point de (P*) placé au-delà ou en deçà de m(x,1) sur la droite (OM), comme E, F ou G, se projette en ce même point m(x,1), perspective de ces points sur (D).

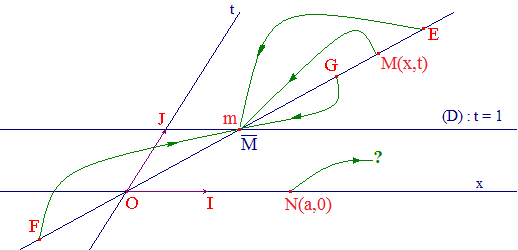
La projection centrale n'est donc pas injective : 2 points distincts peuvent avoir même image. Décidons alors que ces points seront équivalents dans la perspective de centre O relative à (d) en écrivant :

On définit ainsi manifestement une relation d'équivalence dans (P*). La classe d'équivalence, notée ici M de M(x,t) s'identifie alors à m(x,1) et est appelé point projectif. L'ensemble de ces points est la droite projective (D) , notée traditionnellement P(

₂), P pour projectif.

Supposons maintenant que t soit nul, comme pour N(x,0) ci-dessous. ON a alors même direction que OI. Ce cas pose problème car il n'a pas d'image et n'est l'image d'aucun point de (D) puisque (ON) // (D).

C'est ennuyeux mais, intuitivement, en utilisant le principe de perspective énonçant que deux droites parallèles se coupent en un point à l'infini, adjoignons un tel point à (D), notons-le

_D pour exprimer que c'est le point à l'infini de D.

De la sorte, on définit par notre projection une application bijective f :

(D), f(v) = M et on peut identifier (D) à la droite D complétée par son point à l'infini :

Afin de définir un plan projectif, nous devons ici ajouter une dimension et nous placer dans l'espace. Le procédé précédent va nous permettre de construire un plan projectif conforme à la représentation concrète ci-dessous illustrant deux visions d'un pavage du plan : la première est euclidienne (vue d'avion), la seconde est projective (perspective centrale) :

Vision euclidienne

Vision projective d'Alberti

Alberti Leone Battista (1404-1472), savant italien, philosophe, docteur en droit canon (règles régissant la foi catholique basées sur la Bible), peintre, sculpteur et architecte. Il s'intéressa à la perspective en édifiant implicitement les bases de la géométrie projective. La majorité de ses travaux sont malheureusement perdus.

Partant d'une configuration classique de l'espace euclidien 3D, on étudie la perspective de centre 0 relativement au plan (P) parallèle à (xOy) d'équation t = 1. Comme précédemment, toute direction de l'espace (E₃) possède son image dans (P) sauf bien sûr celles définies par tout point N(x,y,0) de (xOy), plan parallèle à (P).

C'est ennuyeux là encore, mais tout aussi intuitivement, en utilisant le principe de perspective énonçant que deux plans parallèles se coupent en une droite à l'infini, adjoignons un telle droite à (P) de la façon suivante :

Considérons le plan (NOK) contenant M(x,y,t), la droite (OM) pivotant vers (ON) dans (NOK) : l'intersection de (OM) avec (NOK) est rejetée à l'infini lorsque M atteint N et ce, dans la direction (ON).

L'ensemble des ces points à l'infini (également dits points impropres) est la classe, notée d

, des points de (xOy). On l'appelle la droite de l'infini. On voit, par construction que cette droite s'interprète comme l'ensemble des directions du plan (P).

On peut maintenant identifier (P) = P(

₃) à au plan (P) complété par la droite de l'infini :

Soit (Q) un plan de l'espace 3D passant par O et (O,u,v) un repère de (Q). En considérant (Q) comme la réunion de toutes les droites passant par O dans le plan (O,u,v), une droite projective (D) s'obtient comme réunion des points projectifs définis par ces droites dans (P).

(D) est aussi la perspective de (Q) dans dans (P). On est en droit d'écrire (D) = (D)

{

_D} où (D) est la droite de l'espace 3D intersection de (Q) et (P). L'équation de (Q) est de la forme ax + by + ct = 0, avec a, b et c non tous nuls. Donc, pour tout t non nul :

On voit ainsi qu'une forme comme ax + by + cz = 0, équation d'un plan dans l'espace affine 3D correspond à l'équation d'une droite dans le plan projectif.

Le point à l'infini de (D) vérifie ax + by = 0, (a,b) distinct de (0,0); c'est la classe des points du plan (xOy) dont un représentant est (b,-a,0). Si (a,b) = (0,0), alors c est non nul : il s'agit du cas (Q) = (xOy).

On se place ici dans l'espace, on considère la perspective de centre O par rapport à un plan (P). Soient A', B' et J' les uniques points d'intersection (ci-dessous) du plan (P) avec les droites respectives (OA), (OB) et (OJ).

Le plan (P) coupe le plan (OAB) suivant une droite (d), c'est donc (A'B'). Mais les plans (OAB) et (OAJ) coïncident. Ainsi (d) est aussi l'intersection de (P) et (OAJ); elle contient donc J' : A', B' et J' sont alignés.

Comme dit plus haut, la projection centrale ne conserve pas le rapport des distances : ce n'est pas une application affine. Mais elle conserve le birapport de quatre points alignés introduit par Desargues et que Chasles appela rapport anharmonique :

Avec les notations de la figure ci-dessus, I et J divisent respectivement le segment [AB] dans le rapport IA/IB et -JA/JB (car JA et JB sont de signes contraires). Le birapport des quatre points A, B, I, J, pris dans cet ordre, est le quotient de ces deux rapports (d'où l'appellation birapport) exprimés en mesure algébrique. On écrira :

La perspective centrale est celle des peintres et des architectes. Elle correspond à ce que voit l'œil : un œil assimilé à un point où convergeraient les rayons lumineux issus du site observé.

Mais la réalité est plus complexe car notre vision binoculaire (deux yeux), aidée par notre cerveau (interpréteur), "voit" le monde en relief. La conservation du birapport s'interprète concrètement comme notre capacité visuelle et cérébrale à évaluer les distances relatives entre les objets et par rapport à nous-mêmes, en tant qu'observateurs.

Preuve de l'invariance du birapport par projection centrale :

Birapport et inversion géométrique :

Attention à l'ordre des points, on ne peut pas écrire n'importe quel birapport ! Dans notre configuration, on remarquera, en passant par la forme produit ci-dessus, que le birapport [A, B, I, J] peut aussi s'écrire IA/JA : IB/JB, soit AI/AJ : BI/BJ, c'est dire que :

Lorsque le birapport vaut -1 (rapport harmonique), donc lorsque IA/IB = -JA/JB, les points sont dits en division harmonique. On dit aussi que I et J divisent harmoniquement le segment [AB] ou encore que I et J sont conjugués harmoniques par rapport à A et B.

Poncelet définira la notion d'homologie et développera celles d'inversion, de polaires d'un point par rapport à un cercle ou à deux droites, de transformation par polaires réciproques et tout particulièrement le principe de dualité (qui fut principalement développé par Gergonne). Ce principe permet d'établir, quasiment sans démonstration, des théorèmes nouveaux en usant les correspondances ci-dessous :

Il en est ainsi par exemple de la droite de Pascal et du théorème de Brianchon, du théorème de Ménélaus et du théorème de Ceva.

L'interprétation projective d'une configuration affine (et vice versa) peut, dans certains cas, permettre d'établir facilement un résultat a priori peu évident. Rappelons la configuration de Pappus :

Démontrons ce résultat en le considérant comme une configuration d'un plan projectif où la droite (ab) est la droite à l'infini (ce qui, en projective, ne restreint pas la généralité) :

La représentation affine équivalente exprime alors le parallélisme des droites (AB') et (A'B) d'une part, (AC') et (A'C) d'autre part.

Il nous faut démontrer que les droites (BC') et (CB') sont parallèles, ce qui impliquera l'appartenance de g à (ab). Deux cas se présentent : les droites (AB) et (A'B') sont concourantes ou parallèles. Le second cas est trivial, considérons le premier. Utilisant la propriété de Thalès, on a les égalités :

En vertu de la réciproque de la propriété de Thalès , Les droites (BC') et (CB') sont parallèles et le théorème de Pappus est ainsi démontré.