ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Symétrie axiale et somme des angles du triangle #1       TD niveau 5ème/4ème      » #2

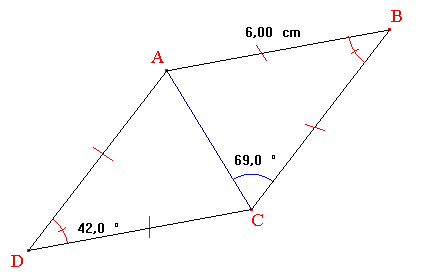
Observe bien cette figure qui ne respecte pas « bien » les codes et valeurs indiqués. C'est fait exprès pour que tu n'affirmes pas des choses sans expliquer car, en fait, le quadrilatère ABCD est un losange !

Pourrais-tu le prouver et construire ensuite, avec soin, une figure plus conforme à la "réalité" en choisissant AB = 6 cm

Solution à compléter :  

1. Calculons tout d'abord les angles ^DAC, ^DCA et ^BAC :

Le codage indique que le triangle DAC est ........... en .....; par conséquent les angles ^DAC et ^DCA ont la .........  ............

Or, dans un triangle, la somme des .............  .....  ............. est égale à .......°. Par conséquent :

 ^DAC = ^DCA = (........ - .....) ÷ 2 = 69°

•  Dans le triangle BAC, on a :

^BAC = 180° - ......° - ......° = 69°

Le triangle ABC est donc aussi ............ de sommet ............. B : c'est dire que BA = ........

2.  Un quadrilatère ayant .......... côtés de ............  .............. est un losange.

Dans notre cas, pour que ABCD soit un losange, il suffit de montrer que ....... = ........

Considérons alors la symétrie d'axe (AC) :

     •  ^BAC = ^DAC : donc [AB) a pour symétrique [......)
     •  ^BCA = ^DCA : donc [CB) a pour symétrique [......)

 Dans la symétrie d'axe (AC), le point B, intersection de [AB) et [CB)  a donc pour symétrique le point ......, qui est l'intersection de [......) et [......). C'est dire en particulier que AB = AD :

ABCD est un losange.

Dans 2., une phrase comme  « les triangles ABC et ACD sont isocèles, ont la même base [AC] et des angles de même mesure, ils sont donc symétriques par rapport à [AC] et  forment par conséquent un losange ABCD » est tout à fait acceptable.