ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Suite & série selon l'Encyclopédie de Diderot et d'Alembert

 ➔   Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension

SERIE ou SUITE, s. f. (substantif féminin) en Algebre, se dit d'un ordre ou d'une progression de quantité qui croissent ou décroissent suivant quelque loi : lorsque la suite ou la serie va toujours en approchant de plus en plus de quelque quantité finie et que par conséquent les termes de cette série, ou les quantités dont elle est composée, vont toujours en diminuant, on l'appelle une suite convergente et si on la continue à l'infini, elle devient enfin égale à cette quantité.

Ainsi 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, etc. forment une suite qui s'approche toujours de la quantité 1 et qui lui devient enfin égale, quand cette suite est continuée à l'infini (série).

→  le texte fait renvoi à différents articles comme CONVERGENCE, APPROXIMATION, ... La distinction entre suite et série sera faite ci-dessous...

La théorie et l'usage des suites infinies a été cultivée de nos jours avec beaucoup de succès; on croit communément que l'invention en est due à Nicolas Mercator de Holstein qui paraît néanmoins en avoir pris la première idée de l'Arithmétique des infinis de Wallis.

On fait usage des suites principalement pour la quadrature des courbes parce que cette quadrature dépend souvent de l'expression de certaines quantités qui ne peuvent être représentées par aucun nombre précis et déterminé; tel est le rapport du diamètre d'un cercle à sa circonférence et c'est un très grand avantage de pouvoir exprimer ces quantités par une suite, laquelle, étant continuée à l'infini, exprime la valeur de la quantité requise.

→  Par quadrature, d'Alembert entend le sens usuel de calcul de l'aire sous une courbe :  » quadrature dans ChronoMath

Nature, origine et usages des suites infinies :     

Quoique l'arithmétique nous donne des expressions très complètes et très intelligibles pour tous les nombres rationnels, elle est néanmoins très défectueuse quant aux nombres irrationnels, qui sont en quantité infiniment plus grande que les rationnels. Il y a par exemple une infinité de termes irrationnels entre 1 et 2 : or que l'on propose de trouver un nombre moyen proportionnel entre 1 et 2, exprimé en termes rationnels, qui sont les seuls que l'on conçoit clairement, la racine de 2 ne présentant certainement qu'une idée très obscure, il est certain qu'on pourra toujours approcher de plus en plus de la juste valeur de la quantité cherchée, mais sans jamais y arriver; ainsi, pour le nombre moyen proportionnel entre 1 et 2 (c'est à dire x vérifiant x/1 = 2/x) , ou (soit) pour la racine carrée de 2 :

• si l'on met d'abord 1, il est évident que l'on n'a pas mis assez;
• que l'on y ajoute 1/2, on a mis trop : car le carré de 1 + 1/2, est plus grand que 2;
• si de 1 + 1/2, l'on ôte 1/8, on trouvera que l'on a retranché trop;
• et si l'on y remet 1/16, le tout sera trop grand.

Ainsi, sans jamais arriver à la juste valeur de la quantité cherchée, on en approchera cependant toujours de plus en plus. Les nombres que l'on vient de trouver ainsi et ceux que l'on peut trouver de la même manière à l'infini, étant disposés dans leur ordre naturel, font ce que l'on appelle une série, ou une suite infinie : ainsi la série :

exprime la valeur de la racine carrée de 2.

→  La convergence de cette série vers la racine carrée de 2 n'est pas évidente car les premiers termes donnés ne permettent pas de conjecturer la suite de la série (attention au jeu de mots involontaire...). Il faut utiliser la formule du binôme de Newton pour les exposants fractionnaires (α = 1/2 et x = 1), qui fournit :

(...)

Mais ce ne sont pas seulement les nombres irrationnels que l'on peut exprimer en termes rationnels par des suites infinies; les nombres rationnels eux-mêmes sont susceptibles d'une semblable expression :

• 1, par exemple, est égal à la suite 1/2 + 1/4 + 1/8 + ...

mais il y a cette différence qu'au lieu que les nombres irrationnels ne peuvent être exprimés en nombre rationnel que par ces suites, les nombres rationnels n'ont pas besoin de cette expression.

Parmi les suites infinies, il y en a quelques unes dont les termes ne font qu'une somme finie; telle est la progression géométrique 1/2, 1/4, 1/8, etc. et en général toutes les progressions géométriques décroissantes : dans d'autres suites, les termes font une somme infinie; telle est la progression harmonique 1/2, 1/3, 1/4, 1/5, etc.

Ce n'est pas qu'il y ait plus de termes dans la progression harmonique que dans la géométrique, quoique cette dernière n'ait point de terme qui ne soit dans la première et qu'il lui en manque plusieurs que cette première contient; une pareille différence rendrait seulement les deux sommes infinies inégales et celle de la progression harmonique serait la plus grande : la raison en est plus profonde; de la divisibilité de l'étendue à l'infini, il suit que toute quantité finie, par exemple un pied, est composée pour ainsi dire, de fini et d'infini :

de fini, en tant que c'est un pied; d'infini, en tant qu'il contient une infinité de parties dans lesquelles il peut être divisé : si ces parties infinies sont conçues comme séparées l'une de l'autre, elles formeront une suite infinie et néanmoins leur somme ne sera qu'un pied : or c'est ce qui arrive dans la suite géométrique 1/2, 1/4, 1/8, etc. décroissante : car il est évident que si vous prenez d'abord 1/2 pied, ensuite 1/2 ou la moitié de ce qui reste, c'est-à-dire 1/4 de pied et puis 1/2, ou la moitié du reste, c'est-à-dire, 1/8 de pied, vous pouvez opérer sans fin, en prenant toujours de nouvelles moitiés décroissantes qui, toutes ensemble ne font qu'un pied.

→ le pied était une unité de mesure valant approximativement 32,4 cm. Le pouce était le douzième du pied. On écrivait à l'époque aussi bien pié que pied. On sait ou, on vérifiera facilement, que 1 + x + x² + ... xⁿ = (1 - xⁿ⁺¹ )/(1 - x); lorsque | x | < 1, xⁿ⁺¹ tend vers 0 et par conséquent 1 + x + x² + ... xⁿ tend vers 1/(1 - x); ici x = 1/2 : 1 + x + x² + ... xⁿ tend vers 2 et 1/2 + (1/2)² + (1/2)³ + ... tend donc vers 1. Voir aussi plus bas.

Quand on dit même que toutes ces parties prises ensemble font un pied, il ne faut pas prendre cette expression à la rigueur, car elles ne feraient un pied que dans la supposition que l'on eût pris tous les termes de la suite et cela ne se peut, puisque la suite est infinie; mais on peut prendre tant de termes de la suite qu'on veut, plus on en prendra, plus on approchera de la valeur d'un pied et quoiqu'on n'ait jamais le pied exactement, on pourra en approcher aussi près qu'on voudra : ainsi cette suite n'a pas proprement un pied pour la somme car une suite infinie n'a point de somme proprement dite puisque sa somme varie selon qu'on en prend plus ou moins de termes et qu'on ne peut jamais les prendre tous.

Mais ce qu'on appelle la somme d'une suite (série), c'est la limite de la somme de ses différents termes, c'est-à-dire une quantité dont on approche aussi près qu'on veut en prenant toujours dans la suite un nombre de termes de plus en plus grand. Nous croyons devoir faire cette remarque en passant, pour fixer l'idée nette du mot de somme d'une suite (série). Revenons à présent à notre suite 1/2, 1/4, 1/8.

Dans cet exemple nous ne prenons pas seulement les parties qui étaient dans le tout, distinguées l'une de l'autre, mais nous prenons tout ce qui y était; c'est pourquoi il arrive que leur somme redonne précisément le tout ou la quantité entière; mais si nous prenons la progression géométrique 1/3, 1/9, 1/27, etc. c'est-à-dire, que nous prenions d'abord 1/3 de pied et que du reste l'on en prenne 1/9 et que de ce dernier reste l'on prenne encore 1/27 de pied, etc.

Il est vrai que nous ne prendrions que les parties qui sont distinctes l'une de l'autre dans le pied mais nous ne prendrions pas toutes les parties qui y sont contenues, puisque nous n'y prenons que tous les tiers, qui sont plus petits que les moitiés; par conséquent, tous ces tiers qui décroissent, quoiqu'en nombre infini, ne pourraient faire le tout et il est même démontré qu'ils ne feraient que la moitié d'un pied.

→ En effet, eu égard au rappel ci-dessus : 1/3 + 1/9 + 1/27 + ... = 1/3(1 + 1/3 + 1/3² + 1/3³ + ...) = 1/3 x 1/(1 - 1/3) = 1/3 x 3/2 = 1/2.

Pareillement tous les quarts, qui décroissent à l'infini (indéfiniment), ne donneraient qu'un tiers pour somme totale et tous les centièmes ne feraient qu'un quatre-vingt dix-neuvième; ainsi, non seulement la somme des termes d'une suite géométrique dont les termes décroissent à l'infini (indéfiniment), n'est pas toujours une quantité finie; elle peut même être plus petite qu'une quantité finie quelconque : car nous venons de voir comment on peut former une suite de quantités qui ne soient égales qu'à 1/2, 1/3, 1/4 et on peut de même en former qui ne soient égales qu'à 1/5, 1/6, etc. 1/10, 1/100, 1/1000, etc. et ainsi à l'infini.

(...)

La géométrie n'est pas sujette, dans l'expression des grandeurs, à autant de difficultés que l'arithmétique : on y exprime exactement en lignes les nombres irrationnels et l'on n'a point besoin d'y recourir aux suites infinies. Ainsi l'on sait que la diagonale d'un carré dont le côté est 1, exprime la racine carrée de 2. Mais en quelques autres cas, la géométrie elle-même n'est pas exempte de ces inconvénients, parce qu'il y a quelques lignes droites que l'on ne peut exprimer autrement que par une suite infinie de lignes plus petites, dont la somme ne peut être déterminée : de cette espèce sont les lignes droites égales à des courbes non rectifiables; en cherchant, par exemple, une ligne droite égale à la circonférence d'un cercle, on trouve que le diamètre étant supposé 1, la ligne cherchée sera 4/1 - 4/3 + 4/5 - 4/7 + 4/9, etc.

→ Car la série 1 - 1/3 + 1/5 - 1/7 + 1/9 - ... converge vers π : » Gregory

Quant à l'invention d'une suite infinie, qui exprime des quantités cherchées, Mercator, le premier inventeur de cette méthode, se sert pour cet effet de la division. Mais M. Newton et M. Leibnitz ont porté cette théorie plus loin; le premier, en trouvant ses suites par l'extraction des racines et le second, par une autre suite présupposée.

Pour trouver, par le moyen de la division, une suite qui soit l'expression d'une quantité cherchée. Supposons qu'on demande une suite qui exprime le quotient de b divisé par a + c, divisez le dividende par le diviseur, comme dans l'algèbre ordinaire, en continuant la division, jusqu'à ce que le quotient fasse voir l'ordre de la progression ou la loi suivant laquelle les termes vont à l'infini; observant toujours les règles de la soustraction, de la multiplication, de la division, par rapport au changement des signes. Quand vous aurez poussé cette opération jusqu'à un certain point, vous trouverez que le quotient est :

→ En effet, en posant la division comme pour une division d'écolier ou celle des polynômes, on obtient :

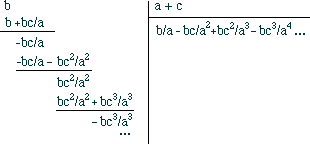
Ces quatre ou cinq termes étant ainsi trouvés, vous reconnaîtrez facilement que le quotient consiste en une suite infinie de fractions. Les numérateurs de ces fractions sont les puissances de c, dont les exposants sont moindres d'une unité que le nombre qui marque la place que ces termes occupent et les dénominateurs sont les puissances de a, dont les exposants sont égaux au nombre qui marque la place de ces termes : par exemple, dans le troisième terme, la puissance de c est du second degré dans le numérateur et la puissance de a est du troisième degré dans le dénominateur.

Par conséquent :

1. Si b = 1 et a = 1, substituant ces valeurs nous aurons le quotient ci-dessus égal à 1 - c + c² - c³ etc. à l'infini : c'est pourquoi 1/(1 + c) = 1 - c + c² - c³, etc. à l'infini.

2. Donc si les termes qui sont au quotient décroissent continuellement, la suite donnera un quotient aussi près du vrai qu'il est possible. Par exemple, si b = 1, c = 1, a = 2, ces valeurs étant substituées dans la suite générale et la division étant faite comme dans l'exemple général ci-dessus, on trouvera :

Supposons maintenant que la série ou la suite s'arrête au quatrième terme, la somme de cette suite sera au-dessous de la véritable; mais il ne s'en faudra pas 1/32. Si elle s'arrête au sixième terme, elle sera encore en dessous, mais moins que de 1/128 : c'est pourquoi plus on poussera la série ou la suite, plus aussi on approchera de la véritable somme, sans pourtant jamais y arriver.

Leibniz et les séries alternées :  »

De la même manière, on trouve que :

• 1/4 = 1/(3 + 1) = 1/3 - 1/9 + 1/27 - 1/81 + 1/243, etc. à l'infini.
• 1/5 = 1/(4 + 1) = 1/4 - 1/16 + 1/64 - 1/256, etc. à l'infini.
• 1/6 = 1/(5 + 1) = 1/5 - 1/25 + 1/125 - 1/625, etc. à l'infini.

Ce qui donne une loi constante, suivant laquelle toutes les fractions, dont le numérateur est l'unité, peuvent être exprimées par des suites infinies; ces suites étant toutes des progressions géométriques qui décroissent en telle manière que le numérateur est toujours l'unité et que le dénominateur du premier terme, qui est aussi l'exposant du rapport, est moindre d'une unité que le dénominateur de la fraction que l'on a proposé de réduire en suite.

Si les termes du quotient croissent continuellement, la série s'éloigne d'autant plus du quotient, qu'elle est poussée plus loin et elle ne peut jamais devenir égale au quotient, à moins qu'on ne limite ce quotient et qu'on ne lui ajoute le dernier reste avec son propre signe.

Par exemple, supposons 1/3 = 1/(1 + 2); on trouvera que le quotient est 1 - 2 + 4 - 8 + 16 - 64 + 128, etc.

• Prenons le premier terme 1 : il excède - 1/3 de 2/3;
• deux termes, c'est-à-dire 1 - 2, seront plus petits de 4/3;
• trois termes seront trop grands de 9/3;
• quatre termes seront trop petits que 1/3 de 15/3, etc.

Si l'on suppose que la série ou la suite se termine au terme - 8, alors on aura :

mais 1 - 2 + 4 - 8 = - 5 = - 15/3; ainsi :

Mais, dira-t-on, qu'exprime donc alors une pareille suite ? car par la nature de l'opération, elle doit être égale à la quantité ou fraction proposée et cependant elle s'en éloigne continuellement. Un auteur nommé Guido Ubaldus (ne serait-ce pas plutôt Guido Grandi) dans son traité De quadratura circuli et hyperbolae, a poussé ce raisonnement plus loin et en a tiré une conséquence fort singulière : ayant pris la suite 1/2 = 1/(1 + 1) et ayant fait la division il a trouvé au quotient 1 - 1 + 1 - 1 + 1 - 1, etc. qui à l'infini ne peut jamais donner que 1 ou 0; à savoir :

• 1, si on prend un nombre impair de termes;
• 0, si on prend un nombre pair.

D'où cet auteur a conclu que la fraction 1/2 pouvait devenir 1 par une certaine opération et que 0 pouvait être aussi égal à 1/2 et que par conséquent la Création était possible, puisqu'avec moins on pouvait faire plus.

L'erreur de cet auteur venait de n'avoir pas remarqué que la suite 1 - 1 + 1 - 1, etc. et en général 1 - c + c² - c³, etc. n'exprimait point exactement la valeur de la fraction 1/(1 + c). Car supposons qu'on ait poussé le quotient de la division jusqu'à cinq termes, comme la division ne se fait jamais exactement, il y a toujours un reste. Soit r ce reste; pour avoir le quotient exact, il faut, comme dans la division ordinaire, ajouter ce reste r divisé par le diviseur 1 + c, à la partie déjà trouvée du quotient.

Ainsi supposons que la série générale soit terminée à -c³, on aura :

1/(1 + c) = 1 - c + c² - c³ + r/(1 + c) = (1 - c² + c² + c³ - c³ - c⁴ + r)/(1 + c)
              = (1 - c⁴ + r)/(1 + c)

1/(1 + c) = 1 - c + c² - c³ + c⁴/(1 + c)

Par conséquent la valeur exacte de 1/2 = 1/(1 + 1) est 1 - 1 + 1 - 1 + 1/(1 + 1) et cette valeur se trouve toujours égale à 1/2 et non pas zéro ou 1. Voyez dans les Mémoires de l'académie de 1715, un écrit de M. Varignon où cette difficulté est éclaircie avec beaucoup de soin.

Pour s'instruire à fond de la matière des suites, on peut consulter le traité de M. Jacques Bernoulli, intitulé Tractatus de seriebus infinitis earumque summa finita, imprimé à Basle (Bâle) en 1714, à la suite de l'Ars conjectandi du même auteur; le septième livre de l'Analyse démontrée du P. Reyneau; l'ouvrage de M. Newton, intitulé Analysis per aequationes numero terminorum infinitas; enfin le traité de M. Stirling, De summatione serierum et celui de M. Moivre, qui a pour titre Miscellanea analytica de seriebus et quadraturis. On joindra à ces ouvrages la lecture d'un grand nombre de mémoires sur cette matière, composés par MM. Euler, Bernoulli etc. etc. imprimés dans les volumes des académies de (Saint-) Petersbourg et de Berlin.

Jean le Rond d'Alembert