ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Une tente bien ventilée    trinôme du second degré TD niveau 2nde /1ère

Dans la fabrication d'une tente canadienne, on veut obtenir une ventilation maximale lorsque l'entrée est ouverte ou la moustiquaire installée. On a schématisé ci-dessous l'entrée de la tente : triangle équilatéral ABC de 2 m de côté.

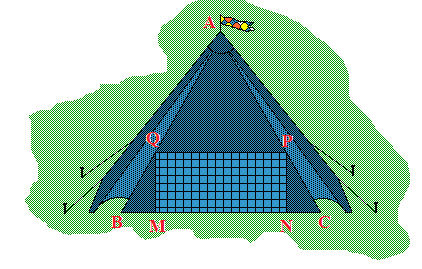
Le rectangle MNPQ inscrit dans ABC correspond à la découpe de la porte. Il s'agit donc de placer M sur [BC] de sorte que l'aire du rectangle MNPQ soit maximale.

Indications pour la solution :    

• On note x = BM. Justifier que le problème revient à rendre maximum le nombre x - x² , lorsque x décrit ]0,1[.

• La recherche de ce maximum pourra se faire très simplement en mettant f(x) = x - x² sous la forme :

f(x) = a - (x - b)²

où a et b sont des constantes positives indépendantes de x que l'on déterminera en développant cette dernière forme et en l'identifiant à x - x². On devra trouver b = 1/2 et a = 1/4.

(x - b)² étant négatif pour toute valeur de x, en déduire la valeur optimale de x.

• En classe de 1ère, on pourra étudier la variation de f sur [0,1] pour constater qu'elle passe par un minimum absolu en x = 1/2, mais la méthode précédente est ici la plus simple.

Réponse : 

La valeur optimale de x est 1/2 et l'aire vaut alors √3/2 , soit une entrée de 1 m de large sur environ 0,87 m de haut (c'est la demi-hauteur de la tente). On note que, contrairement à ce que l'on pourrait intuitivement conjecturer, la forme trouvée n'est pas un carré.