
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» fonction elliptique , courbe elliptique |
Les intégrales elliptiques (qualificatif dû à Legendre en 1793), sont nées de la volonté de calculer la longueur d'un arc d'ellipse (rectification de l'ellipse), dont le précurseur, dans ces travaux, après Jakob Bernoulli et sa lemniscate, fut Fagnano. Étudiées par Gauss et Lagrange, ces intégrales firent l'objet d'une nouvelle approche par Abel avec la définition des fonctions elliptiques (Recherches sur les fonctions elliptiques, 1826). Legendre et Jacobi s'emparèrent également brillamment et indépendamment du sujet à la même époque. Legendre et Jacobi s'emparèrent également et indépendamment du sujet à la même époque. Tannery et Molk ont également brillamment traité le sujet à la fin du 19è siècle (4 volumes, 1893-1902, » réf.10).
Considérons une ellipse
d'équation cartésienne réduite (a > b) : 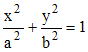 et passons en coordonnées coordonnées paramétriques
et passons en coordonnées coordonnées paramétriques

On pose en général x = a.cost et y = b.sint, mais préférons ici, afin de "coller" plus bas aux formules de Legendre, la paramétrisation équivalente :
x = a.sint et y = b.cost
En t = 0, on sera en B(0,b) et en t = π/2, en A(-a,0).
On différencie : dx = a.cost et dy = -b.sint et on reporte dans la formule calculant la longueur d'un arc infinitésimal ds2 = (dx)2 + (dy)2 en remarquant que cos2t = 1 - sin2t :
ds2 = a2 + (b2 - a 2)sin2t = a2 - (a2 - b2)sin2t = a2(1 - e2sin2t)
où e2 = 1 - b2/a2 désigne le carré de l'excentricité e de l'ellipse. Pour tout t compris entre 0 et π/2 (arc du second quadrant) on aura :

En posant z = sin u, on est conduit au calcul d'une intégrale de la forme
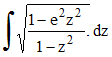
C'est un cas particulier d'intégrale elliptique de deuxième espèce.
| Classification actuelle des intégrales elliptiques : |
Plus généralement, on démontre que toute intégrale elliptique, c'est à dire, selon Lagrange, une intégrale de la forme :
![]()
avec F fonction rationnelle (quotient de deux polynômes) et p un polynôme du 4è degré sans zéro multiple, se ramène à trois types fondamentaux, exhibés par Legendre (0 < e < 1), et dont Liouville prouva qu'aucun ne peut s'exprimer par quadrature au moyen de fonctions élémentaires :
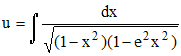 ,
dite de 1ère
espèce (ou du 1er ordre)
,
dite de 1ère
espèce (ou du 1er ordre)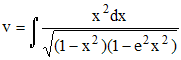 ,
dite de 2ème
espèce (ou
du second ordre)
,
dite de 2ème
espèce (ou
du second ordre)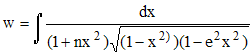 ,
dite de 3ème
espèce (ou du 3ème ordre)
,
dite de 3ème
espèce (ou du 3ème ordre)Le nombre e, souvent noté k dans les tables, est appelé module et n est le paramètre. Noter que si n = -1, w peut s'exprimer en fonction de u et v. De même si n = - k2.
i Lorsque le polynôme p est de degré supérieur à 4, une intégrale dont l'intégrande est de la forme P/√Q avec d°Q >4, on parle d'intégrales hyperelliptiques. Elles furent étudiées en particulier par Goursat dont on pourra lire un mémoire (1885) en cliquant sur le lien ci-dessous :
Sur la réduction des intégrales hyperelliptiques : » Intégrales abéliennes : »
En posant x = sin φ (φ est l'amplitude; pour l'ellipse, φ représente l'anomalie excentrique), on obtient alors les formes équivalentes (0 < k < 1) :
1ère espèce :
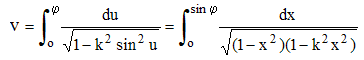
Cette intégrale intervient dans le calcul de la longueur d'un arc d'hyperbole : afin d'obtenir le même radical en u (qu'il nomme
Δ) dans les 3 espèces, Legendre, ramène l'équation à la forme x2/a2 - y2/b2 = 1 et a2 + b2 = 1 , on paramètre en posant y = btan t. On pourra lire les calculs page 16 de cette référence (texte de Legendre, Google livres) dont un extrait est donné ci-dessous.2ème espèce :
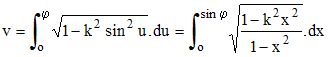
Comme on l'a vu ci-dessus, ce type intégrale est censé fournir la longueur de l'ellipse (ou d'un arc de cette courbe fermée) lorsque k = e < 1 excentricité de l'ellipse. Vu que e2sin2u est alors strictement inférieur à 1, on peut développer en série, ce qui conduit à :
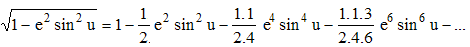
que l'on intègre terme à terme en linéarisant au préalable les puissances de sin u (linéarisation très prisée des élèves de Terminale S...) si on ne pousse pas trop le développement... ou en utilisant l'intégrale de Wallis :
Calcul approché de la circonférence de l'ellipse par développement en série : »
➔ Ce type d'intégrale se retrouve dans le calcul de la longueur d'un arc de sinusoïde, d'équation y = sin x en appliquant la formule relative aux équations cartésiennes, l'intégrande est alors :
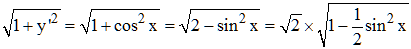
Vous êtes ainsi amené à calculer une intégrale du type v ci-dessus avec un coefficient multiplicateur √2 et k = √2/2.
3. 3ème espèce :
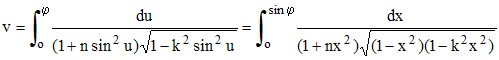
Legendre donna une formulation plus simple de ces intégrales en posant :
![]()
Ultérieurement, Gudermann posa, par analogie avec le cercle :
Les fonctions θ (thêta) de Jacobi : »
| Fonctions circulaires et fonctions elliptiques : |
La difficulté de l'étude des intégrales elliptiques amena Abel à étudier le problème "inverse". Si une intégrale elliptique est de la forme :
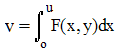
v est une fonction de u. En posant u = ψ(v), on définit (dans des conditions de validité à préciser) par inversion, une fonction elliptique, fonction réciproque v. En élargissant l'étude de ces fonctions au cas d'une variable complexe, Abel constate une propriété surprenante :
l'existence de deux périodes incommensurables T1 et T2 ! On dit qu'une telle fonction f est doublement périodique pour signifier que :le quotient T1/T2 n'es pas un nombre réel et f(z + T1) = f(z) et f(z + T2) = f(z)
∗∗∗
Gauss et Jacobi seront les premiers à poursuivre les travaux d'Abel, mort prématurément à l'âge de 27 ans et Weierstrass semble être le premier à avoir construit un exemple de telles fonctions, appelé fonction P, fonction méromorphe définie par une série
(» réf.11).De nos jours, indépendamment de leur genèse, on peut définir une fonction elliptique en tant que fonction méromorphe doublement périodique.
Fonction holomorphe, fonction méromorphe : »
En quelque sorte (et en bien plus compliqué), les fonctions elliptiques sont à l'ellipse ce que les fonctions trigonométriques usuelles, dites circulaires, sont au cercle : en effet, considérons le cercle unité d'équation x2 + y 2 = 1. Pour x élément de [o,1], on vérifie facilement que l'on a pour la longueur d'un arc du premier quadrant :
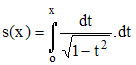
On pourrait qualifier s(x) "d'intégrale circulaire". On remarque que l'intégrande (fonction sous le signe d'intégration) est la fonction dérivée de la fonction Arcsin et s apparaît ainsi comme réciproque de la fonction circulaire sinus.
|
Notion de courbe elliptique : |
Une courbe elliptique est une courbe algébrique sans point multiple que l'on peut paramétrer au moyen de fonctions elliptiques. L'appellation est due à Joseph Serret (1843). Elles jouent encore aujourd'hui un rôle important en théorie des nombres (équations diophantiennes) en se ramenant à rechercher des points à coordonnées entières ou rationnelles sur de telles courbes (» réf. 5). Leur plus bel usage fut sans doute la preuve du fameux grand théorème de Fermat démontré par Andrew Wiles en 1995 et, sur un plan plus pratique, on les retrouve aujourd'hui en cryptographie (» réf. 6), cachées dans les algorithmes de sécurité (bancaire en particulier).
De façon élémentaire, on peut en donner ainsi la définition :
On appelle courbe elliptique une courbe algébrique du troisième degré (cubique) dont l'équation peut se ramener à la forme :
où le second membre, polynôme du 3ème degré en x, n'a pas de solution double.
➔ On ne s'étonnera pas de l'absence des x2 dans le membre de droite : on vérifiera qu'une équation du type y2 = x3 + ax2 + bx + c se ramène à la forme donnée par changement d'origine en posant X = x - a/3 et Y = y.
∗∗∗
Montrer que la condition x3 + ax + b
n'a pas de solution double se résume à 4a3 + 27b2 ≠ 0
La notion générale de courbe algébrique : » Résolution de l'équation du 3ème degré : »

Posons p(x) = x3 + ax + b. Les courbes définies par y2 = p(x) sont symétriques par rapport à l'axe des abscisses : on a y = ±√p(x). Elles s'étudient relativement facilement en étudiant tout d'abord le signe de x → p(x), relevant de l'équation algébrique du 3ème degré, puis le sens de variation de x→√p(x). Voici un cas admettant deux composantes dont l'une est fermée :

Le cas ci-dessus se produit lorsque le polynôme p admet trois racines réelles. Voici en superposition la courbe en question et celle de son polynôme :

Courbes elliptiques et 7è problème du 21è millénaire : » » Plücker , Mordell , Bhargava , Wiles
➔ Pour en savoir plus :
 ABRÉGÉ D'HISTOIRE DES MATHÉMATIQUES, 1700-1900,
Jean Dieudonné
ABRÉGÉ D'HISTOIRE DES MATHÉMATIQUES, 1700-1900,
Jean Dieudonné
Ch 7, Fonctions elliptiques et intégrales abéliennes
par Ch. Houzel,
Ed. Hermann, Paris - 1992
Dictionnaire des mathématiques
: Algèbre, Analyse, Géométrie
Ouvrage extrait de l'Encyclopædia Universalis, Ed. Albin Michel, Paris, 1997
Le rang des courbes elliptiques par François Brunault (ENS Lyon) sur Images des mathématiques avec l'étude du groupe des points à coordonnées rationnelles : http://images.math.cnrs.fr/Le-rang-des-courbes-elliptiques.html
Courbes elliptiques (dont courbes supersingulières), applications à la cryptographie par Stéphane Ballet et Alexis Bonnecaze (École Polytech. Marseille) : https://alexis-bonnecaze.pedaweb.univ-amu.fr/CryptoAvancee.pdf
Algèbre des fonction elliptiques, Géométrie des ovales cartésiennes, par Évelyne Barbin & René Guitard, univ. Paris7), 2001 : http://archive.numdam.org/article/RHM_2001__7_2_161_0.pdf
Traité des fonctions elliptiques et des intégrales
eulériennes, Adrien Legendre sur Google Livres :
http://books.google.fr/books?id=vaAKAAAAYAAJ&printsec=frontcover&dq=legendre+fonctions+elliptiques+...