ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

KUMMER Ernst Eduard, allemand, 1810-1893

Né à Sorau (alors ville prussienne, aujourd'hui Zary, en Pologne), fils de médecin décédé alors qu'il n'avait que trois ans, après un début d'études de théologie voulu par sa mère à l'université de Halle proche de Sorau, Kummer se consacre aux mathématiques et obtient son doctorat en 1831. Il commença sa carrière comme professeur de lycée en sa ville natale, puis à Leignitz (actuelle Legnica, Pologne) dès l'année suivante. Kronecker, Du Bois-Raymond et Cantor furent parmi ses élèves.

Il fut ensuite nommé à l'université de Breslau (1842). A la mort de Gauss (1855), Dirichlet, qui enseignait à l'université de Berlin, lui succède à Göttingen, laissant ainsi sa place à Kummer. Le poste de Breslau ainsi vacant fut repris par Weierstrass. Kummer enseigna parallèlement la balistique à l'École de guerre de Berlin. Il est par ailleurs  à l'origine de la mise en place, avec Weierstrass, du séminaire de mathématiques de Berlin en 1861.

Ses travaux portèrent sur les séries et les équations différentielles mais son nom est resté célèbre par ses recherches en algèbre et en arithmétique. Avec Kummer naît une nouvelle approche de l'arithmétique : la théorie algébrique des nombres. Ses travaux conduiront Kronecker et Dedekind à l'étude des corps de nombres algébriques. Weber et Hilbert apporteront une contribution essentielle sur ce sujet au début du 20è siècle.

Les nombres idéaux et le théorème de Fermat :

Poursuivant des travaux de Gauss, Kummer travailla de nombreuses années sur la célèbre conjecture de Fermat, appelée parfois grand ou dernier théorème, selon laquelle xn + yn = zn  n'a pas de solutions entières (x,y,z) ≠ (0,0,0) pour n > 2. Il crut l'avoir démontrée en 1845. Sa méthode novatrice, poursuivie par Kronecker, bouleversa l'arithmétique traditionnelle et conduira Dedekind aux fécondes notions d'anneau et d'idéal d'anneau (que formalisera Fraenkel en 1914) et au développement de la théorie des corps de nombres algébriques.

Dans le cas élémentaire n = 2, l'équation x2 + y2 = z2 peut s'écrire dans l'anneau Z(i) = {a + bi, (a,b)∈Z2} des entiers de Gauss :

z2 = (x + iy)(x - iy)

et la recherche de z2 sous forme d'une somme de carrés peut être substituée à la décomposition de z2 dans Z(i). Mais des nombres premiers dans Z ne le sont parfois plus dans cet anneau, ce qui peut signifier la remise en question de l'unicité de la décomposition en facteurs "premiers" :

Factorisation et divisibilité dans un anneau : »          Extensions algébriques de R et C : »

On voit là le besoin d'étudier une nouvelle arithmétique dans ce type de nombres. Le français Lamé, mais principalement Kummer, travaillent sur le sujet. Dans le cas général de l'équation de Fermat, il s'agit de rechercher les décompositions éventuelles de xn = zn - yn  (n premier) en un produit :

xn = (z - u1y)(z - u2y)...(z - uny)           (1)

où les ui désignent les racines n-èmes de l'unité et d'étudier le problème d'une factorisation unique en produit de « facteurs premiers ». Si r désigne une racine n-ème primitive de l'unité (qui engendre leur groupe) on peut écrire :

xn = (x - y)(x - ry)(x - r2y)...(x - rn-1y)           (2)

et si l'arithmétique de Z s'applique dans Z(r), la suite du raisonnement consiste à prouver que les facteurs x - rky du produit sont premiers 2 à 2 et que chaque facteur est alors lui-même une puissance n-ème dans Z[r]. Puis par un processus proche de la descente infinie, on aboutit à une contradiction.

En fait, la "preuve" de Kummer fut mise à mal par Cauchy qui s'aperçut que si n = 23, la factorisation dans Z(r) n'est pas unique. Le résultat de Kummer s'avéra valable que pour une certaine classe de nombres premiers n, dits réguliers dont les propriétés se rattachent aux nombres de Bernoulli. Il put alors valider la conjecture pour les exposants premiers inférieurs à 100, autres que 37, 59, 67.

Polynôme et corps cyclotomiques :

Dans l'usage de l'anneau Z(r) Kummer eut recours à un concept nouveau : l'introduction de ses nombres idéaux, un artifice garantissant l'unicité de la décomposition en produit de facteurs encore appelés premiers et conduisant à une théorie nouvelle basée sur le corps de dislocation du polynôme P(x) = (x - u1)(x - u2)...(x - uφ(n)) des racines n-ièmes primitives de l'unité (φ(n) est le totient d'Euler).

Ce polynôme, dit cyclotomique (forgé sur le grec, mot à mot qui découpe le cercle) car les images de ses racines ui, engendrant leur groupe, sont solutions dans C de l'équation Xn = 1 et donc représentées sur le cercle unité. Le polynôme P est unitaire, de degré φ(n) et  irréductible sur Q. Si n est premier, n ≥ 3, on a φ(n) = n - 1.

 ➔   L'extension algébrique simple Q(uk) engendrée par l'une quelconque des racines n-ièmes est qualifié de corps cyclotomique.

L'idée de tels polynômes avait été utilisée par Vandermonde dans son mémoire de 1771 dans le but de prouver que l'on pouvait résoudre l'équation xn = 1 par radicaux, c'est à dire exprimer les racines de l'unité au moyen de radicaux arithmétiques. Il s'était attaché en particulier au cas n = 11 que l'on peut ramener au 5è degré.

Corps de nombres algébriques : »        Structures algébriques : »        Nombres p-adiques : »
Divisibilité dans un anneau commutatif unitaire, idéal d'anneau, idéal premier : »

»  Dedekind , Kronecker , Weber , Hilbert , Bell

En reconnaissance de ses recherches, Kummer reçut (1857) la médaille d'or du grand prix de Mathématiques de l'Académie des Sciences : en 1823, l'Académie avait déclaré offrir une forte récompense en monnaie or à celui qui démontrerait la célèbre conjecture, aujourd'hui définitivement élevée au rang de théorème (1993) grâce à Andrew Wiles.

Critère de Kummer :

Soit une série Σun à termes positifs. S'il existe une suite (an) de réels positifs telle que la suite de terme général :

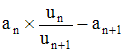
converge vers un réel L, alors si L > 0 la série est convergente, si L < 0 la série est divergente. Le cas L = 0 est litigieux.

Critère de Raabe-Duhamel : »           Critère de d'Alembert  : »            Séries numériques  : »

Équation différentielle de Kummer, fonctions de Kummer, surfaces de Kummer :

♦  Dans le domaine de la physique mathématique, il s'agit de l'équation différentielle linéaire du second ordre où K est une fonction de la variable complexe z :

zK'' + (γ - z)K' - αK = 0

C'est un cas particulier de l'équation de Riemann également étudiée par Gauss. Cette équation possède trois singularités. On parle ici d'équation confluente car deux de ces singularités "confluent" en une seule. Par transformation homographique, on peut se ramener au cas où l'une est en 0 et l'autre à l'infini.

 i  Le mathématicien et astronome anglais Edmund Whittaker (1873-1956), professeur à Edimbourg, et Ernst Lindelöf étudièrent également ce difficile sujet.

Les solutions, dites fonctions de Kummer,  sont des fonctions hypergéométriques Σunzn  :

           »  fonction gamma Γ

∗∗∗
a) Que devient K lorsque α = γ dans N ?
b) Vérifier que K est effectivement hypergéométrique, c'est à dire que un+1/un est une fonction rationnelle de n

Fonctions hypergéométriques de Gauss : »          Équation et fonctions Jn de Bessel : »

♦  Surface de Kummer (1864) : surfaces algébriques de degré 4, de genre 2, possédant 16 points doubles réels (le maximum pour une telle surface). On peut donner une équation cartésienne d'une telle surface dans R3 sous la forme (source : » réf.1&2 ci-dessous) :

(x2 + y2 + z2 - µ2w2)2 - λpqrs = 0, µ2 > 1

p = w - z - x√2 , q = w - z + x√2 , r = w + z + y√2 , p = w + z - y√2 (coordonnées "tétraédriques"), λ = (3µ2 - 1)/(3 - µ2). Le cas µ2 = 1 correspond à une surface de Steiner. Une particularité supplémentaire d'une surface de Kummer est de posséder 16 plans tangents contenant chacun 6 de ses points doubles situés sur une conique.

 

 ➔  Pour en savoir plus sur les surfaces de Kummer :

  1. Kummer surfaces, par Stephan Endrass : http://www2.mathematik.uni-mainz.de/alggeom/docs/Ekummer.shtml

  2. Kummer surfaces, par Max Kutler (Yale university) : https://www.math.hmc.edu/~ursula/teaching/math189/finalpapers/max.pdf

  3. Sur le site Mathcurve de Robert Ferréol : https://www.mathcurve.com/surfaces/kummer/kummer.shtml

  4. https://archive.org/details/184605691/page/n9, par Ronald Turnbull (univ. Cambridge, 1905)

Peirce Benjamin  Galois
© Serge Mehl - www.chronomath.com