ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Notion
de
géométrie
non euclidienne et géométrie de l'univers |
Considérons un segment [AB]. Élevons les segments isométriques [BC] et [AD] perpendiculaires à [AB]. Joignons C et D. On obtient un quadrilatère de Saccheri, du nom d'un philosophe et mathématicien italien du qui s'intéressa au bien fondé de l'axiomatique euclidienne :
S'il vous semble évident que ABCD est un rectangle (ce qui est aussi mon avis), il vous faudra, pour le prouver, utiliser le 5è postulat d'Euclide (axiome des parallèles) :
Par un point situé hors d'une droite, on ne peut faire passer qu'une seule parallèle à cette droite
Les quatre premiers postulats d'Euclide permettent de prouver l'égalité des angles ^C et ^D. Le cinquième permet de prouver que ces angles sont droits. Inversement si nous admettons que ces angles sont droits, alors ils sont égaux (4è postulat) et le 5è postulat en découle. En géométrie euclidienne plane, le plus court chemin d'un point à un autre est un segment de droite. Encore faut-il savoir ce qu'est une droite... Plus généralement, on parle de géodésique : courbe tracée sur une surface minimisant la distance entre deux de ses points.
Il y a ainsi 3 hypothèses :
♦1 - Celle de l'angle droit :
^C et ^D sont droits et nous obtenons la géométrie
euclidienne
élémentaire (géométrie plane et
géométrie de l'espace) où la somme des angles d'un triangle est
égale à deux droits.
♦2 - Celle de l'angle obtus : ^C et ^D sont obtus et nous obtenons la géométrie de Riemann, dite sphérique (et plus généralement elliptique) où les droites sont ses grands cercles (cercles équatoriaux de même centre que la sphère, également appelés méridiens).
Deux droites quelconques se rencontrent donc en deux points (deux pôles de la sphère) et deux points A et B de la sphère de centre O définissent une unique droite, à savoir le méridien intersection de la sphère avec le paln (AOB). Les "triangles" tracés sur la sphère ont pour côtés des segments de droites, c'est à dire ici des arcs de grands cercles. On parle de triangle sphérique.
Dans
cette géométrie, la somme des angles d'un triangle est supérieure à 180° : sur
le dessin de droite, le triangle dont les côtés
sont des quarts de méridiens possède déjà deux angles droits ! Deux méridiens se
coupant en S à angle droit définissent un triangle dont les 3 angles sont droits
!
Albert Girard et la notion de triangle sphérique : »
Pour aller d'un point à un autre de la sphère par le chemin le plus court (chemin orthodromique), il faut suivre le grand cercle passant par ces points : ligne géodésique de la sphère et non pas aller à cap constant (chemin loxodromique). C'est le principe utilisé en navigation maritime et aérienne.
Depuis les années 1990, époque où l'ex URSS autorisa le survol de son immense territoire, de nombreux vols intercontinentaux se sont avérés beaucoup plus courts, donc beaucoup plus économiques, en suivant un méridien passant par le pôle nord (ou à proximité) : S désignant ce dernier, il en est ainsi lorsque le point de départ D et le point d'arrivée A définissent "sensiblement" un méridien : le plan (DSA) contient le centre de la Terre assimilée à une sphère. On pourra consulter le lien ci-dessous ainsi que le joli petit logiciel de Geneviève Tulloue en réf. 10 in fine : pour un vol New York / Shang Hai, on gagne plus de 5000 km par voie orthodromique !
Géodésique, loxodromie et orthodromie : »
♦3 - Celle de l'angle aigu : ^C et ^D sont aigus et nous obtenons la géométrie de Lobatchevski, dite aussi de Bolyai, entrevue par Gauss et étudiée également par Beltrami, dont une représentation peut être donnée sur la pseudosphère, (schématisée ci-dessous), surface de révolution engendrée par une tractrice et de courbure totale négative constante dont une équation est :
x = cos(u)/ch(v) , y = sin(u)/ch(v) , z = v - th(v)
En rouge, ce sont des droites de cette géométrie : géodésiques de la surface (plus court chemin d'un point à un autre), à savoir les tractrices qui engendrent la surface et qui sont à la pseudosphère ce que sont les grands cercles de la sphère (méridiens). Sur cette surface, la somme des angles d'un triangle est inférieure à 180° (» réf.2 & 3).
La mise en place de telles géométries non euclidiennes (appellation due à Gauss), cohérentes (s'avérant sans contradictions logiques), montra l'indépendance du célèbre 5è postulat d'Euclide vis à vis des quatre autres. C'est Félix Klein qui assurera leur classification dans son programme d'Erlangen en 1872. Il montra que les géométries non euclidiennes peuvent être interprétées comme des géométries projectives sur une surface conique, d'où la terminologie qu'il utilisa :
Interprétation plane (plan hyperbolique), Disque de Beltrami et de Poincaré, métrique de Cayley : »
La géométrie différentielle, initiée par Gauss et développée par Riemann, avec la notion de courbure des surfaces, permettra de concrétiser ces nouvelles géométries.
La courbure d'un plan (en
géométrie euclidienne) est nulle et les chemins minimisant les
distances sur cette
surface (géodésiques) sont ses droites. Pour tout triangle ^A + ^B + ^C =
180°.
La sphère possède une courbure totale positive constante; ses
"droites" (géodésiques") sont les grands cercles (méridiens).
Pour tout triangle ^A + ^B + ^C > 180°.
La pseudosphère
est une surface à courbure totale négative constante.
Pour tout triangle ^A + ^B + ^C < 180°.
Il en est de même du paraboloïde hyperbolique en forme de "selle de cheval" :
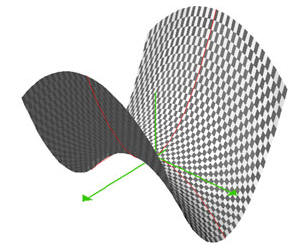
Courbure totale (ou gaussienne) : »
| Géométrie non euclidienne et nature géométrique de l'Univers : |
Ces
nouvelles géométries s'avèrent adaptées
à l'étude de notre univers où l'on a pu
constater que la matière "courbe" l'espace dans lequel elle
évolue (trous noirs, rayons lumineux au voisinage du
Soleil), corroborant la théorie de la relativité
générale (1916) d'Albert
Einstein (1879-1955) dans une conception non
euclidienne de l'espace.
i Albert Einstein sur WikipédiA
Il fut prouvé qu'admettre l'homogénéité de l'univers (propriétés identiques en tout point au même instant) et son isotropie (propriétés en tout point indépendantes de la direction), ce qui est apparait conforme aux observations actuelles, équivalait à une courbure constante de ce dernier, mais on ne sait toujours pas si cette courbure est positive ou négative.
D'autant qu'en 2013, à l'étonnement général, les observations du satellite Planck (mission franco-européenne), semblent montrer que cette courbure est nulle ou tout au plus "extrêmement" faible : en trois mots l'univers est euclidien !
Résumons :
♦ Si la courbure est positive, notre univers relève de la géométrie elliptique et il est fini, topologiquement équivalent, comme le pensait Einstein, à une sphère de dimension 3 (hypersphère). Il relève alors de la géométrie envisagée par Riemann.
Hypersphère de dimension n : »
♦ Si la courbure est négative, note univers relève de la géométrie hyperbolique de Lobatchevski et il est infini.
♦ Si la courbure est nulle, note univers relève de la géométrie euclidienne de l'illustre Euclide d'Alexandrie et il est peut-être infini...
En savoir un peu plus sur le Big-bang, Albert Einstein, Max Planck et notre Univers : »
➔ Pour en savoir plus (liens externes) :
par Albert Einstein, Éd. Petites bibliothèque Payot, Paris - 1956
,
best-seller de Stephen Hawking (1988), rééd. 2008, Éd. Champs sciences.
,
par Stephen Hawking, Éd. Odile Jacob, poches Sciences, Paris, 2000.
par divers contributeurs, Éd. du
Seuil.