ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Exemples classiques de surfaces et leurs équations
    » Notion de surface | les différents types d'équation d'une surface | cas du ruban de Möbius

♦ Le tore de révolution :    


Une vieille chambre à air...

Cette surface de révolution est engendrée par la rotation d'un cercle autour d'un axe situé dans son plan et ne le coupant pas. Comme l'explique la figure ci-dessous, en se plaçant dans un repère orthonormé (O,x,y,z) de l'espace euclidien et en posant OA = a et AM = r avec 0 < r < a,  A décrit le cercle de centre O, de rayon a dans le plan (xOy) tandis que M(x,y,z) décrit le cercle de centre A, de rayon r dans le plan (AOz). L'équation paramétrique du tore s'écrit alors :

x = (a + r.cos u)cos v , y = (a + r.cos u)sin v , z = r.sin u

  

où u et v varient de 0 à 2π. Le rayon du cercle générateur est r, le rayon de giration étant a : distance de l'axe au centre du cercle générateur.

   

 ➔  Un tore n'est pas toujours de révolution; on peut envisager des surfaces toriques lui ressemblant à un homéomorphisme près. Il en est ainsi de la représentation à facettes, à droite ci-dessus, obtenue au moyen d'un logiciel 3D ou de cette vieille chambre à air étirée... :

Sections d'un tore et d'un plan, équation cartésienne du tore : »         

♦ L'hélicoïde :      

Également appelée vis d'Archimède. C'est une surface réglée qui fut étudiée par Euler. Son équation paramétrique est du type :

x = αu.cos v , y = αu.sin v , z = β.v

où α et β sont des constantes. Le paramètre u varie de 0 à R, R désignant le rayon de l'hélicoïde qui s'inscrit dans un cylindre droit de rayon R; v désigne le nombre de tours, multiple de 2π. Mis à part le plan, c'est la seule surface minimale réglée.

♦ L'ellipsoïde et la sphère :    

Il s'agit d'une quadrique dont l'équation cartésienne peut se mettre sous la forme :

x2/a2 + y2/b2 + z2/c2 = 1

Lorsque deux des paramètres a, b et c sont égaux, on parle de sphéroïde comme ci-dessous (c'est sensiblement le cas de notre planète, sphère aplatie) : la section par un plan parallèle à (xOy) est un cercle. Dans le cas général, on obtient une ellipse.

 ➔  Si a = b = c, on obtient une sphère (du grec sphaira = balle, ballon) de rayon a, dont l'équation se résume à  x2 + y2 + z2 = a2 :

 !  On ne la confondra pas avec la boule de rayon a qui n'est pas une surface mais un volume, d'équation x2 + y2 + z2 ≤ a2, réunion de la sphère et de son intérieur.

En utilisant les coordonnées curvilignes, une équation paramétrée de l'ellipsoïde (sphère si a = b = c) peut s'écrire :

x = a.cos u.cos v , y = b.sin u.cos v , z = c.sin v

et par suite, celle de la sphère de rayon R = a = b = c :

x = Rcos u.cos v , y = Rsin u.cos v , z = Rsin v , u ∈ [0,2π], v ∈ [-π/2,+π/2]

Une telle surface peut être engendrée par une ellipse (dite génératrice) centrée sur Oz, située dans un plan parallèle à (xOy) et soumise à toucher, en se déplaçant, deux ellipses (dites directrices) centrées en O, dont les axes sont dirigés par Ox et Oz d'une part, Oy et Oz d'autre part d'équations, dans leurs plans respectifs, x2/a2 + z2/c2 = 1 , y2/b2 + z2/c2 = 1.

 ➔  On peut aussi obtenir un ellipsoïde de façon simple : par révolution d'une ellipse autour d'un de ses axes (cas a = b). Il s'apparente à la surface d'un ballon de rugby.


Fontaines ellipsoïdales, centre commercial Carré Sénart (Seine & Marne)

Ombilics de l'ellipsoïde : »           Conque sonore : »  

♦ L'hyperboloïde à une nappe :       

Il s'agit là encore d'une quadrique dont l'équation cartésienne peut se mettre sous la forme

x2/a2 + y2/b2 - z2/c2 = 1

 ➔  On appelle nappe d'une surface, toute partie connexe de cette surface. Rappelons qu'un espace E est connexe s'il est, intuitivement d'un seul tenant : topologiquement, il ne peut exister exister une partition de E en deux ouverts (ou deux fermés) non vides.    

   
Centrale nucléaire de Tricastin (Drôme) & châteaux d'eau aux environs de l'aéroport de Roissy (France)

On engendre une telle surface en soumettant l'ellipse génératrice du cas précédent à "toucher" cette fois deux hyperboles encore centrées en O dont les équations dans leurs plans respectifs, (xOz) et yOz), sont :

x2/a2 - z2/c2 = 1 , y2/b2 - z2/c2 = 1

 ➔  L'hyperboloïde peut être de révolution : obtenu par rotation d'une branche d'hyperbole autour d'un de ses axes; son équation est alors de la forme :

x2/a2 + y2/a2 - z2/c2 = 1    (b = a)

A partir de cette équation, on peut obtenir une paramétrisation au moyen des coordonnées curvilignes, l'équation de l'hyperboloïde de révolution peut s'écrire :

Preuve : posons z = cu, u décrivant R. Compte tenu de l'égalité x2/a2 + y2/a2 - z2/c2 = 1, dans le plan (xOy) la projection d'un point M(x,y,z) de la surface est le point m(x,y) décrivant le cercle de centre O de rayon a√(1 + u2). on peut donc poser x = a√(1 + u2)cos v et y = a√(1 + u2)sin v avec v décrivant [0,2π].

Hyperboloïde en tant que surface réglée : »

♦ L'hyperboloïde de révolution à deux nappes :      (» nappe)

Quadrique, surface algébrique du second degré, dont l'équation cartésienne peut se mettre sous la forme :

x2/a2 + y2/a2 - z2/c2 = -1

La génération est identique au cas précédent (hyperboloïde à une nappe) mais cette fois les hyperboles directrices ont pour équation :

x2a2 - z2/c2 = -1 , y2/a2 - z2/c2 = -1

En paramétrant, l'équation peut s'écrire au moyen des coordonnées curvilignes :

x = a.sh(u).cos v, y = a.sh(u).sin v , z = ± c.ch u

Preuve : la cote z décrit R. Posons z = ± c.ch u, u décrivant R; compte tenu de l'égalité x2/a2 + y2/a2 - z2/c2 = -1, dans le plan (xOy) la projection d'un point M(x,y,z) de l'hyperboloïde est le point m(x,y) décrivant le cercle de centre O d'équation x2 + y2 = ch2u - 1 = sh2u, de rayon a.sh u. On peut donc poser x = a.sh u.cos v et y = a.sh u.sin v avec v décrivant [0,2π].

On peut aussi obtenir l'hyperboloïde à deux nappes par rotation des deux branches d'une hyperbole autour de l'un de ses axes :

∗∗∗
On suppose (ci-dessous), que l'on fait tourner autour de (Oy) l'hyperbole d'équation y2/4 - z2 = 1 tracée dans le plan (yOz)


Soit M(x,y,z) un point de la surface obtenue. Montrer qu'une équation de l'hyperboloïde est : x2 + z2 - y2/4 = - 1

♦ Le cylindre :     

Un grand classique connu depuis les années collège... On peut le considérer comme la réunion des droites parallèles (génératrices) s'appuyant sur une courbe (c). On imagine aisément les formes très variables d'un cylindre : il peut être prismatique si la courbe (c) est un polygone. » prisme.

Toutes les représentations du cylindre sont évidement limitées en "hauteur". Mais, en principe, elle ne l'est pas car il est engendré par une droite. C'est dire que toute représentation "finie" revient à le considérer comme engendré par un segment de droite.


 ce cylindre s'appuie sur une lemniscate de Bernoulli

Le plus connu est le cylindre de révolution (ci-dessous) correspondant au cas où (c) est un cercle de centre O, (OS), appelé axe du cylindre, étant perpendiculaire au plan du cercle. En principe, sa "hauteur" n'est pas limité. On a représenté, ci-dessous, un cylindre de révolution d'axe Oz, de rayon 2, de hauteur 2 (cote z comprise en 0 et 2). Si son axe se confond avec l'axe (Oz), l'équation paramétrée du cylindre s'écrit très simplement : tout point du cylindre se projette sur (xOy) en un point du cercle de centre O de rayon 2; donc x = 2cos u , y = 2sin u. Quant à la cote z, elle varie de 0 à 2. On peut donc écrire :

x = 2cosu , y = 2sinu , z = v  u variant de 0 à 2π et v de 0 à 2

Son équation cartésienne peut s'écrire x2 + y2 = 2,  0 ≤ z ≤ 2.

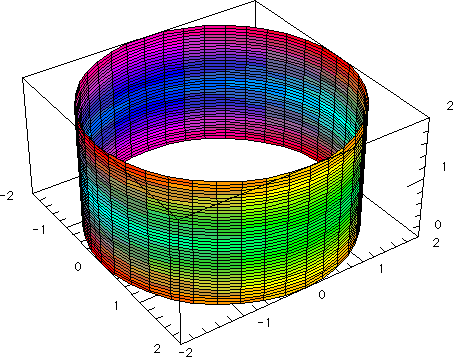
 ➔  Coordonnées cylindriques :    

Remarquer que tout point M de l'espace tridimensionnel peut être repéré par sa projection en coordonnées polaires sur le plan xOy et sa cote z : M(rcosu, rsinu ,z) : on parle de coordonnées cylindriques.

Hélice circulaire, géodésique du cylindre : »      Coordonnées cylindriques et sphériques (cartographie) : »

∗∗∗
Justifier que l'on peut considérer un plan comme un cylindre !

  Paraboloïde cylindrique : »              Cas du ruban de Möbius : »

♦ Le cône de révolution :      

Un cône est la réunion des droites (génératrices), passant par un point donné S (sommet) et une courbe (c) appelée directrice.

Le cas du cône de révolution ou cône circulaire droit correspond à celui où (c) est un cercle de centre O, (OS) appelé axe du cône, étant perpendiculaire au plan du cercle. (c) n'est pas unique : tout cercle centré sur (OS) dont un rayon aboutit sur une génératrice engendrera le même cône.  C'est dire que ce dernier peut être caractérisé par l'angle α (demi-angle au sommet) entre son axe et une de ses génératrices.

 ➔  Si M(x,y,z) est un point du cône, alors m(kx,ky,kz), k non nul, est aussi un point du cône. Une équation cartésienne d'un cône du type f(x,y,z) = 0 est donc homogène de degré 2.

L'exemple ci-dessous correspond (sensiblement) à α = 40°. Tout point situé à la même cote z décrit un cercle (c). Un petit calcul de trigonométrie élémentaire fournit z2 = (x2 + y2) × cotan2α, soit :

 x2 + y2 - z2tan2α = 0

∗∗∗
Montrer que x2 = yz est l'équation d'un cône de sommet O dont la courbe directrice est la parabole y = x2 dans le plan z = 1.

∗∗∗
Ci-dessous est représenté un cône de révolution limité par sa "base", cercle de rayon 1, et sa "hauteur" égale à 3.
Vérifier qu'une équation paramétrique en est :
x = (1 - v/3)cos u , y = (1 - v/3)sin u , z = v, u variant de 0 à 2π et v de 0 à 3
 » utiliser que pour chaque cote z = v, le rayon r de révolution vérifie ici r/1 = (3 - z)/3.

♦ Le paraboloïde hyperbolique :      

Également appelé selle de cheval, son équation peut s'écrire, à la cote z (ligne de niveau) :

z = x2/a2 - y2/b2

Cette surface est souvent donnée comme exemple de surface à courbure constante négative.

       

La voûte hyperbolique en selle de cheval est souvent utilisée en architecture contemporain. Exemple : Guillaume Gillet (1912-1987), architecte de la cathédrale de Royan et, ci-dessus, de l'église Saint-Joseph-Travailleur près d'Avignon.

Paraboloïde elliptique, indicatrice de Dupin : »

 ➔   Pour en savoir plus :

  1. Cours de mathématiques, tome 1, Ch. 21 par Jean Bass - Ed. Masson et Cie - Paris, 1964.

  2. ABRÉGÉ D'HISTOIRE DES MATHÉMATIQUES, sous la direction de Jean Dieudonné
    Ch IX, Géométrie différentielle par Paulette Libermann - Ed. Hermann

  3. ATLAS DES MATHÉMATIQUES, Fritz Reinhardt, Heinrich Soeder, Ch. géométrie différentielle
    La Pochothèque - Le Livre de Poche (collection Encyclopédies d'aujourd'hui), 1997

  4. APPLICATION DE L'ANALYSE A LA GÉOMÉTRIE, Gaspard Monge
    Les cours historiques de l'Ecole Polytechnique (1807) - Ed. MARKETING (ellipses) - 1994

  5. Courbes et Surfaces, Que sais-je ?, n° 564 par Jean Taillé, P.U.F.

  6. Très beau site site (et très complet) de Robert Ferreol : des surfaces et leurs équations, mais aussi des courbes
    2D, 3D, des polyèdres :  http://www.mathcurve.com/surfaces/surfaces.shtml

  7. Le site de Xah Lee : http://xahlee.org/PageTwo_dir/more.html

  8. Le site de Xiao Gang pour tracer vos propres courbes ou surfaces :
     http://wims.unice.fr/~wims/wims.cgi?session=XGD2CBA318.3〈=fr&module=tool%2Fgeometry%2Fanimtrace.fr (...)

  9. Parmi les logiciels de Denis Monasse, un programme remarquable gratuit, utilisé pour cette page : Surface2.

© Serge Mehl - www.chronomath.com