ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Notions sur les
courbes gauches
» Tangente | Plan osculateur et normale principale | Courbure (courbes planes & gauches) Torsion | Trièdre de Frenet | » Cas des surfaces (orientation, trièdre de Ribaucour, courbure) |
Une
parabole,
une sinusoïde
sont des courbes planes. Une ellipse,
un cercle sont des courbes
planes fermées. Pour ces exemples, tous les points des courbes
considérées sont situés dans un
même plan : une courbe est dite
gauche
(gauchir = dévier, tordre) s'il n'en est pas ainsi. C'est une
courbe dans l'espace euclidien usuel à trois
dimensions dont un des premiers grands spécialistes français fut
Alexis Clairaut.
Un exemple simple de courbe gauche est donné par un ressort, la vrille d'un tire-bouchon, la forme de l'escalier en colimaçon d'une tour (en hélice). L'intersection de deux surfaces (par exemple une sphère et un cylindre) est généralement une courbe gauche.
➔ Dans toute la suite, pour faciliter l'écriture, les vecteurs sont écrits en gras.
Dans un repère orthonormé (0,i,j,k) de l'espace, un arc de courbe gauche (c) s'étudie paramétriquement par :
où M(u) est un point de (c) dépendant du paramètre u. Les fonctions f, g et h, abscisse, ordonnée et cote de M, sont des fonctions de u au moins une fois continûment dérivables (classe C1).
| Abscisse curviligne (plan & espace) : |
On se place dans le cas dit régulier où les dérivées f ', g' et h' de f, g et h (définissant OM ci-dessus) ne s'annulent pas simultanément : la courbe (c) n'admet ni point multiple (elle ne se traverse pas) ni point de rebroussement et, lorsque u varie, M se déplace toujours dans le "même" sens d'une extrémité à l'autre de l'arc.
Rebroussement & inflexion : »
Dans ces conditions le calcul différentiel et intégral permet de calculer la longueur de l'arc AM et on peut orienter la courbe de sorte que cette longueur soit une fonction strictement croissante de u : sens positif de parcours. Si on note A le point origine de l'arc, la mesure de l'arc AM(u) est l'abscisse curviligne, notée s(u) du point M(u).
En choisissant s comme paramètre, l'étude d'un arc régulier peut alors se ramener à celle du vecteur :
AM(s) = x(s).i + y(s).j + z(s).k
noté souvent simplement M(s) une fois l'origine des arcs choisie. L'introduction de s facilite l'étude des tangentes et de la courbure :
|
Tangente en un point, vecteur tangent : |
De façon analogue à la notion élémentaire de tangente à une courbe plane, la tangente en un point M(u) s'obtient comme position limite d'une sécante en M(u) et M(u + h) lorsque h tend vers 0. Lorsque cette limite existe, un vecteur directeur de la tangente en M est alors colinéaire à T (dx/du, dy/du, dz/du), c'est à dire aussi T (f '(u), g'(u), h'(u)).
» Noter que ce vecteur ne dépend pas de l'origine A des arcs : si B est un autre point origine : BM = AM - AB et dAM/du = 0.
En remarquant que :
on constate que le vecteur tangent T est aussi colinéaire au vecteur de coordonnées (dx/ds, dy/ds, dz/ds) et ce dernier ne dépend pas de l'origine A des arcs.
Dans toute la suite, on notera τ le vecteur unitaire tangent en M(s); il est colinéaire à :
♦ Si la courbe gauche est définie paramétriquement sous la forme x = f(u), y = g(u), z= h(u) la tangente en M(a,b,c) correspondant à u = uo est dirigée par T(f '(uo),g'(uo),h'(uo)); son équation paramétrique est alors x - a = λ.f '(uo), y - b = λ.g'(uo), z - c= λ.h'(uo) et en éliminant λ, la tangente aura pour équation :
(x - a)/f '(uo) = (y - b)/g'(uo) = (z - c)h'(uo)
! si les trois dérivées sont nulles, il s'agira d'un point singulier. Sinon, il conviendra d'annuler le numérateur d'un membre dont la dérivée est nulle.
♦ Si la courbe gauche est définie comme intersection de deux surfaces f(x,y,z) = 0 et g(x,y,z) = 0, la tangente en M(a,b,c) est la droite d'intersection des plans tangents en M, c'est donc la droite définie par :
les dérivées partielles étant prises au point M(a,b,c).
| Plan osculateur et normale principale : |
La difficulté de l'étude des courbes gauches résulte du fait que le point M qui la parcourt change de plan : contrairement aux courbes planes, parler de normale à la courbe est ambigu : tout vecteur orthogonal en M à la tangente τ est candidat.
Il existe cependant un plan remarquable (P) contenant τ que l'on peut obtenir comme position limite (si elle existe) du plan défini par trois points de (c) infiniment proches M(s), M(s + h) et M(s + k) lorsque h et k tendent vers 0 : c'est le plan osculateur (du latin osculor, osculatus = caresser) à (c) au point M(s).
➔ Un plan tangent touche une courbe en un point (deux points confondus). Le plan osculateur (P) fait mieux : en général, il touche en deux points.
Le vecteur n = dτ/ds = d2M/ds2 est un vecteur de base unitaire de ce plan orthogonal à τ, appelé normale principale en M(s). On peut ainsi définir (P) en tant que plan (M,τ, n).
|
Trièdre (ou repère) de Frenet : |
Afin de faciliter l'étude locale d'une courbe de l'espace, Frenet eut l'idée d'étudier la courbe dans un repère mobile d'origine M(s). Dans l'espace euclidien orienté c'est le triplet (τ , n, b) où :
τ désigne le vecteur tangent (normé) orienté dans le sens des abscisses curvilignes croissantes;
n est la normale principale (normée);
b = τ ^ n est la binormale (produit vectoriel de τ par n).
Le plan (M, n,b ) est le plan normal en M. Le plan (M, τ, b ) est le plan rectifiant.
Étude du trièdre de Frenet, formules de Frenet : »
|
Courbure d'une courbe (plane ou gauche), rayon de courbure, cercle osculateur : |
On conçoit qu'un cercle de rayon R possède une certaine courbure ne dépendant que de son rayon : son rayon de courbure... Il s'agit ici de définir la courbure pour une courbe quelconque. Le schéma ci-dessous permet de comprendre que la courbure entre deux points "proches" M(s) et M(s + Δs) peut se mesurer au moyen de l'angle Δâ formé par les tangentes en ces points qui correspond à l'angle des plans normaux en ces deux points. On se ramène alors à une unité d'arc :
Définitions :
La courbure K en un point M(s) est définie comme la limite, lorsque Δs tend vers 0, du rapport Δâ/Δs :
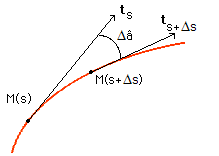
La courbure d'un cercle de rayon R est constante et égale 1/R. En effet, l'angle Δâ de deux tangentes proches se retrouve en ^AOB. La longueur du cercle est 2πR. On a donc Δs = 2πR × Δâ/2π. soit : K(s) = dâ/ds = 1/R et si R devient infini, la courbure tend vers 0. On retrouve ce résultat souvent énoncé : une droite peut être considérée comme un cercle de rayon infiniment grand.
Rayon de courbure :
D'une façon générale, le rayon de courbure ρ en un point d'une courbe est l'inverse de la courbure.
Centre et cercle de courbure, cercle osculateur :
Le centre de courbure est la position limite de l'intersection des deux normales en M(s) et M(s+Δs) et on parle alors de cercle de courbure ou cercle osculateur (du latin osculor, osculatus = caresser).
Comme dans le cas du cercle, le centre de
Le cercle osculateur est tangent à la courbe au point considéré. Il est clair qu'une infinité de cercles possèdent alors cette propriété. Ce qui distingue le cercle osculateur, c'est d'avoir le même rayon de courbure que la courbe. En d'autres termes :
Dans le cas d'une courbe plane, Δâ s'interprète comme différence entre les angles formés par ces tangentes avec l'axe des abscisses. On a donc tan â = dy/dx (= y' dans le cas cartésien) et le rayon de courbure ρ en un point de la courbe s'évalue relativement facilement selon le type d'équation :
1- cartésienne M[x,f(x)] :
ρ = (1 + y'2)3/2/y"
car â = Atn y', donc dâ/dx = y"/(1+y'2). Or ds = (dx2 + dy2)½ = dx(1 + y'2)½
ρ = (x'2 + y'2)3/2/(x'y" - y'x")
3 - implicite f(x,y) = 0 :
par dérivation implicite : y' = - f ' x/f 'y
et y" = - (f ''xx + 2y'f ''xy + y'2f ''yy)/f ''y. Puis utiliser 1.
ρ = (r2 + r'2)3/2/(r2 + 2r'2 - rr")
➔ si (α',β',γ') sont les coordonnées de n (normale principale unitaire), les coordonnées du centre de courbure en M(x,y,z) sont alors :
|
Torsion ou seconde courbure : |
Cette notion est propre aux courbes gauches et mesure comment la courbe se "tord" en changeant de plan. Dans le trièdre de Frenet, elle correspond à l'angle des plans osculateurs P(s) et P(s + Δs) en deux points infiniment proches M(s) et M(s + Δs), donc à l'angle Δû entre les binormales mesurant comment la courbe se tord en passant de P(s) à P(s + Δs). Ainsi, de façon analogue à la courbure, la torsion T en un point sera, par unité d'arc, la limite lorsque Δs tend vers 0 du rapport Δû/Δs :
Le calcul d'une torsion est donc, a priori, le calcul de la mesure d'un angle de l'espace. A l'instar de la courbure et du rayon de courbure, on parle du rayon de torsion, ρ = 1/T, inverse de la torsion.
Au 19è siècle, l'analogie avec la courbure conduisit les mathématiciens à appeler seconde courbure cette torsion qui, grâce à Frenet, se réduit à un calcul différentiel. Voir, en exemple, la courbure et la torsion de hélice circulaire.
➔ Pour en savoir plus :