ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Convexité      » fonctions convexes | ensembles & espaces convexes , parties étoilées | espaces localement convexes | simplexes

Une partie P d'un espace affine E est dite convexe si, pour toute paire de points A et B de P, le segment [AB] est inclus dans P.

• Un disque du plan (resp. une boule de l'espace euclidien 3D) est convexe mais le cercle (resp. la sphère), sa surface, ne l'est pas.

• Tout polygone convexe est convexe... :-)

• Une lunule ou un tore ne sont pas convexes.

• Une surface ou un volume de l'espace usuel contenant des parties "concaves" ou des trous ne sont pas convexes.

 ➔  Par segment, on entend l'ensemble des points M de P tels que AM = λAB, 0 ≤ λ ≤ 1, soit, dans le plan ou l'espace euclidien usuel, les points de la droite (AB) situés entre A et B (extrémités A et B comprises).

Mathématiques au jardin.... :
panneau dit "convexe" (B), panneau dit "concave" (C) extrait du catalogue Gedimat, Aménagements extérieurs 2007.       

On peut obtenir une définition symétrique en A et B en remarquant que la relation précédente peut s'écrire :

(1 - λ)MA + λMB = 0, 0 ≤ λ ≤ 1       (2)

équivalente à :

αMA + βMB = 0, α et β positifs       (3)

C'est dire que le segment [AB] est l'ensemble des barycentres de A et B à pondération positive.

Si l'espace E est muni d'une origine O La relation (2) peut aussi s'écrire au moyen de la formule de Chasles sous la forme :

OM = (1 - λ)OA + λOB, 0 ≤ λ ≤ 1

Il résulte de cette écriture que si A et B sont deux points d'une droite d'origine O contenant un point M, en notant a, b et x les abscisses respectives de A, B et M, on a l'équivalence :

M∈[AB]   ⇔  x = (1 - λ)a + λb, λ∈[0,1]

 ➔  Vu que [AB] = [BA], on peut évidemment échanger les rôles de A et B : M∈[AB]   ⇔  x = λa + (1 - λ)b, λ∈[0,1]

• Si E et F sont des espaces affines et f une application affine de E vers F, alors toute image directe ou réciproque d'une partie convexe est convexe.

• Toute intersection de parties convexes est convexe.

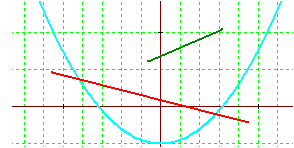
• La réunion de parties convexes n'est généralement pas convexe : l'hexagone et l'ellipse ci-dessous sont convexes, leur intersection l'est aussi mais non pas leur réunion.

♦  Théorème de Helly :    

Soit C₁, C₂ ..., C_p une famille finie de convexes de Rⁿ avec p ≥ n + 1. Si toute intersection de n + 1 d'entre eux est non vide, alors l'intersection des p éléments de la famille est non vide.

• Dans le plan, considérons une famille de p disques (p ≥ 3). Si 3 quelconques d'entre eux se rencontrent, alors l'intersection de tous les disques contient au moins un point.

» Hörmander

On dit qu'une fonction numérique f est convexe sur un intervalle réel J = [a,b] de son ensemble de définition pour exprimer que :

f [(1 - λ)a + λb] ≤ (1 - λ)f(a) + λf(b),  λ∈[0,1]      (cvx)

On peut dire que f est sous-additive relativement à tout point de [a,b].

En particulier :   

 Si f est convexe sur J = [a,b], alors pour tout α et β de J, on a :

♦  Épigraphe, Hypographe :   

Dans un repère du plan contenant une courbe (c) représentative d'une fonction numérique f, on qualifie d'épigraphe l'ensemble des points M(x,y) du plan tels que y ≥ f(x) et d'hypographe l'ensemble des points M(x,y) vérifiant y ≤ f(x). La courbe (c) apparaît comme intersection de son épigraphe et de son hypographe.

Avec cette définition, on peut énoncer :

f est convexe si et seulement si son épigraphe est convexe

Concrètement (ci-dessous) la courbe représentative de f sur [a,b] est "en-dessous" du segment [AB] joignant les images de a et de b (y = f(x) ≤ z) : la courbe présente un creux : on parle parfois de concavité tournée vers le bas. Concavité ? Mais qu'est-ce à dire ?

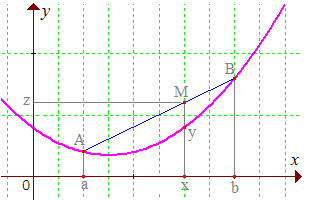
♦  Fonction concave :   

Une fonction numérique est dite concave lorsque son opposé -f est convexe. Et on remarquera que :

f est concave si et seulement si son hypographe est convexe

 ➔  Le graphique ci-dessus est un arc de parabole. Une telle courbe partage le plan en deux régions : pour toute paire de points A et B de la parabole, le segment ]AB[ est intérieur à la parabole. Tout point non intérieur est à l'extérieur de la parabole. On remarquera la relativité des sens que l'on peut donner à concave et convexe dans le langage courant :  une petite bête extérieur à la parabole dira "qu'elle est convexe" (bombée), une petite bête à l'intérieur dira "qu'elle est concave"...   

»  Chemin optique & miroir convexe | Chemin optique & miroir concave

Eu égard à la définition mathématique d'une partie convexe, l'intérieur de la parabole est convexe mais non pas son extérieur comme l'indique en exemple le segment rouge :

  i   Une additivité, égalité au lieu de ≤ dans la définition de la convexité (cvx), signifierait que la fonction f est affine sur [a,b] : f(x) serait de la forme mx + p. On a dans ce cas, en notant que p = (1 - λ)p + λp :

f [(1 - λ)a + λb] = m[(1 - λ)a + λb] + (1 - λ)p + λp =  (1 - λ)(ma + p) + λ(mb + p) = (1 - λ)f(a) + λf(b)

∗∗∗
Montrer inversement que si f [(1 - λ)a + λb] = (1 - λ)f(a) + λf(b),  λ∈[0,1], alors les images de l'intervalle [a,b] sont "alignées" au sens que si M(x,f(x), alors les vecteurs AM et BM sont colinéaires. En déduire que la restriction de f à l'intervalle [a,b] est affine.

Inflexion en un point d'une courbe plane : »

♦  Fonctions convexes sur espace vectoriel abstrait :   

On généralise la définition d'une fonction convexe sur un espace vectoriel réel E en tant que fonction numérique telle que :

∀ (u,v) ∈ E² : f [(1 - λ)u + λv] ≤ (1 - λ)f(u) + λf(v),  λ∈[0,1]         (cvx2)

∗∗∗
Montrer qu'une semi-norme sur un espace vectoriel E est une fonction convexe sur E

Résultats fondamentaux :   

Soit f une fonction numérique définie sur un intervalle ouvert J fini ou non de R .

1. Si f est continue sur J,  f convexe ⇔ f [½(a + b)] ≤ ½[f(a) + f(b)] pour tous a et b de J

2. Théorème de Stolz : 
     
   a) Si f est convexe sur J alors f est continue sur J et dérivable à gauche et à droite en tout point de J.
   b) De plus, l'ensemble des points de non dérivabilité de f est fini ou dénombrable.

 i  Otto Stolz (1842-1905) : mathématicien autrichien qui étudia les mathématiques à Innsbruck et à Berlin. Weierstrass y fut un de ses professeurs. Professeur à Innsbruck, Ses travaux portent sur l'analyse, la théorie des fonctions de plusieurs variables. On lui doit notamment Grundzüge der differential und integral Rechnung (Éléments de calcul différentiel et intégral) en 3 volumes édités entre 1893 et 1899 à Leipzig. » théorème de Stolz pour les intégrales doubles, Fréchet.

3. f est convexe si et seulement si son taux d'accroissement en tout point a de J est croissant sur J :



4. Si f est dérivable, f convexe ⇔ f ' croissante

5. Si f  est deux fois dérivable : f convexe ⇔ f ''≥ 0.

6. Toute combinaison linéaire finie de fonctions convexes est convexe.

7. Toute limite f d'une suite de fonctions convexes est convexe.

∗∗∗
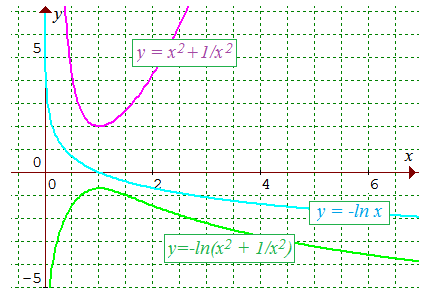
1°. Justifier que les fonctions x → - ln(x)  et u : x → x²+1/x² sont convexes sur R₊* (ln désigne le logarithme népérien).
En est-il de même de x → - ln(u(x)) ?  Ind. : non, - ln(u) change de concavité en x = (4+√17)^1/4 ≈ 1,69.


2°. Soit f strictement positive sur J, deux fois dérivable en tout point de J. Montrer que ln f(x) est convexe si et seulement :
pour tout x de J :  [f '(x)]² ≤  f(x)f ''(x).  Ind. : calculer  [ln f(x)]'' et utiliser 5.

De façon analogue au cas concret des espaces affines, on peut parler de segment dans un espace vectoriel (E,+,.) sur le corps K = R ou C : u et v désignant deux vecteurs de E, le segment [u,v] d'extrémités u et v sera défini ainsi :

w∈[u,v]   ⇔  w = (1 - λ)u + λv, λ∈[0,1]

i/ Une partie A de E est dite convexe si pour toute paire {u,v} d'éléments de A, le segment [u,v] est inclus dans A.

• E lui-même est convexe;

• Si E est normé, toute boule (ouverte ou fermée) est convexe;
• Toute intersection (finie ou non) de parties convexes est convexe.

ii/ Une partie A de E est dite étoilée lorsque E contient au moins un élément u tel que pour tout v de E le segment [u,v] soit inclus dans A. On dira aussi que A est étoilée par rapport à v.

A est convexe si et seulement si elle est étoilée par rapport à chacun de ses éléments

Théorème de Poincaré sur les formes différentielles : »

Lorsque E peut être muni d'une topologie (au moyen d'une norme ou d'une semi-norme par exemple), il est important de pouvoir travailler en termes de voisinages convexes. On dira que E est localement convexe lorsque chaque élément de E possède un système fondamental de voisinages convexes.

• Un espace de Fréchet, par exemple, peut se définir comme un espace topologique localement convexe, métrisable et complet.  

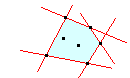
Lorsque E est un espace affine et P une partie de E, l'ensemble des parties de E contenant P n'est pas vide : il contient E. L'intersection de toutes les parties de E contenant P est appelé enveloppe convexe de P. C'est le plus petit convexe contenant P.

• L'enveloppe convexe d'une paire de points {A,B} est l'intervalle [AB];

• Dans le plan euclidien, l'enveloppe convexe d'un nombre fini P de points de E est le domaine polygonal convexe fermé d'aire minimale que l'on peut obtenir en joignant des points de P (par des droites formant les côtés).

Dans l'espace, on obtiendrait de façon semblable un polyèdre convexe au moyen de plans formant les faces et en dimension supérieure à 3 au moyen d'hyperplans. On parle alors de polytope, concept relativement récent dû à Alicia Stott.

 i  Alicia Stott : mathématicienne amateur (1860-1940), fille de George Boole. Sans recevoir une formation mathématique supérieure, elle s'intéressa aux mathématiques, et tout particulièrement, en géométrie, aux polyèdres archimédiens et à une interprétation de la géométrie en dimension 4, dans un article, On certain series of sections of the regular four-dimensional hypersolids, publié à Amsterdam en 1900. Ses travaux ne furent que partiellement reconnus jusqu'à sa rencontre (1930, elle a alors 70 ans), avec un jeune mathématicien anglais de l'époque Harold S. M. Coxeter (1907-2003) passionné par le sujet. » source.

Rappelons qu'on appelle hyperplan d'un espace affine de dimension n, toute variété (sous-espace) affine de dimension n - 1.

• Dans le plan, les droites sont les hyperplans de dimension 1;

• Dans l'espace 3D (dimension 3), les hyperplans sont les sous-espaces affines de dimension 2 : ce sont donc les plans.

• L'hypercube est est un polytope de l'espace à 4 dimensions. Il est au cube de l'espace usuel 3D ce que ce que ce dernier est au carré de l'espace 2D. Sa perspective dans l'espace 3D fut présentée par Gardner en 1977. La voici (en 2D...) :

Perspective dans le plan de l'hypercube selon Coxeter : »

♦  Notion de simplexe :     

On considère dans Rⁿ l'ensemble fini P constitué de n + 1 points, trois quelconques d'entre eux n'étant pas alignés. On appelle simplexe l'enveloppe convexe de P. Les points de P sont les sommets.

Si n = 1, on a un segment, si n = 2, il s'agira d'un triangle, si n = 3 d'un tétraèdre, si n > 3, on parlera là encore de polytope. L'étude des simplexes est un très important chapitre de la topologie combinatoire dont le théorème d'Euler-Descartes est un exemple. On les retrouve en particulier dans les problèmes de programmation linéaire avec la méthode du simplexe du mathématicien et informaticien américain Georges B Dantzig qu'il développa dès 1947.

Simplexe des parties d'un ensemble : »

Un exercice élémentaire de programmation linéaire : »            »  Dantzig

 ➔  Pour en savoir plus :

1. N. Bourbaki, Livre IV, Espaces vectoriel topologiques, Ch. 1, fonctions convexes et espaces localement convexes.
   On en trouvera une version historique sur Mathdoc à l'adresse :
   http://portail.mathdoc.fr/archives-bourbaki/PDF/000_iecnr_002.pdf

2. ENCYCLOPÆDIA UNIVERSALIS, tome2, Éd. Albin Michel, Paris, 1997/98

3. Convexité par Michel Berger : Convexité dans le plan, dans l'espace et au delà (2 fascicules)

4. Simplexes et polytopes : http://www.dma.ens.fr/~debarre/Aussois.pdf. Voir aussi :
   http://www.dma.ens.fr/~debarre/Colloquium.pdf

5. Simplexes et complexes simpliciaux par H. Cartan sur le site Numdam :
   http://www.numdam.org/item?id=SHC_1948-1949__1__A1_0

6. Sur les premiers travaux d'Alicia Boole (American Mathematical Society) :
    http://www.ams.org/featurecolumn/archive/boole.html

7. Alicia Boole et les polytopes de dimension 4 :
    http://dissertations.ub.rug.nl/FILES/faculties/science/2007/i.polo.blanco/c5.pdf

8. Description de l'hypercube sur YouTube :
   #1 : Stéréogramme 3D de l'hypercube : http://www.youtube.com/watch?v=LPLj7t1IVLk
   » observer l'image brouillée en louchant progressivement et en vous rapprochant lentement de votre écran.
   #2 : http://www.youtube.com/watch?v=ccws454YiVM
   #3 : http://www.youtube.com/watch?v=2pRZCoWY6TU