ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Suites et fonctions hypergéométriques |
Les séries hypergéométriques furent initiées par Gauss. Ce sont des séries entières, à termes réels ou complexes, de la forme Sunzn où le rapport un+1/un des coefficients de deux termes consécutifs est une fonction rationnelle de n.
L'appellation hypergéométrique provient du fait qu'on généralise ainsi celle de série géométrique Sazn où le rapport un+1/un est une constante a.
Exemple : si un+1/un = 1/(n + 1) et uo = 1, on a alors un = 1/n! et la série hypergéométrique converge donc vers ez.
La fonction exponentielle et son
développement en série :
En 1812, Gauss obtient dans ses recherches en physique mathématique l'équation différentielle linéaire (qui apparaîtra ultérieurement comme un cas particulier d'équation de Riemann) :
z(z - 1)F" + z(a + b + 1)F' - gF' + aby = 0
dont la recherche d'une solution F sous forme de série entière Sunzn, au voisinage de z = 0, le conduit à la relation de récurrence :
(n + 1)(n + g)un+1 = (n + a)(n + b)un
Pour z réel ou complexe, on obtient alors, à un facteur multiplicatif près, lorsque g est non nul et distinct de tout entier négatif :
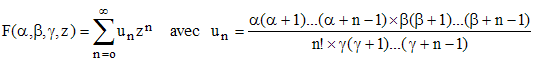
soit, pour les 4 premiers termes :
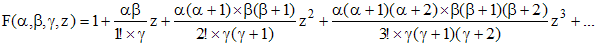
Pour p entier et
quelconque, on écrit parfois
x(x + 1)(x + 2)...(x + p - 1) = (x)p
notation pratique due au mathématicien allemand Leo August Pochhammer (1841-1920), élève de Kummer, qui étudia les séries hypergéométriques dans un cadre plus général.
Si x et p sont des entiers naturels, on a (x)p = (x + p - 1)!/(x - 1)! Avec cette notation, on a alors :
un = (a)n(b)n / n!(g)n.
Séries hypergéométriques généralisées :
http://mathworld.wolfram.com/GeneralizedHypergeometricFunction.html
Un cas élémentaire :
Lorsque b = g , on a :
F(1,b,b,z) = 1 + z + z2 + ... zn + ...
Il s'agit de la série géométrique de raison z convergeant vers 1/(1 - z) si | z | < 1.
Montrer que : xF(1,1,2,-x)
= ln(1 + x) , Asin x = xF(½,½,3/2,x2)
,
cosx = F(½,-½,½,sin2x)
, ex = lim b
F(1,b,1,x/b)
En utilisant cette propriété de la fonction G d'Euler, on peut vérifier que F(a,b,g,z) peut s'écrire :
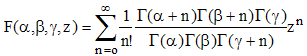
Ces fonctions connurent un important développement jusqu'à nos jours car utilisées dans de nombreuses applications mathématiques ou physiques et dans des cas particuliers d'inversion d'intégrales elliptiques :
Par exemple, la fonction elliptique de 1ère espèce :
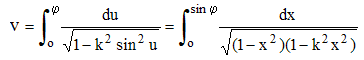
Lorsque j =½p, on peut montrer que : u = ½pF(½,½,1,k2). De même, la fonction elliptique de 2ème espèce :
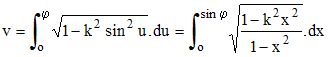
s'écrit de façon simple au moyen de la fonction hypergéométrique : v = ½pF(-½,½,1,k2).
Les fonctions hypergéométriques permettent également d'exprimer les polynômes orthogonaux comme ceux de Legendre ou de Hermite par exemple. Elles sont à rapprocher des fonctions Jn de Bessel rencontrées en mécanique céleste (perturbations des orbites) et dans des phénomènes oscillatoires de la physique
Équation et fonctions Jn de Bessel :
Équation de Kummer :
