
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Variété topologique, atlas et carte locale | Variété riemannienne | Variété lisse | Surfaces de Riemann |
Suite aux travaux novateurs de Gauss dans l'étude des surfaces, Riemann développa ce qui devint une branche maîtresse des mathématiques : la géométrie différentielle. L'objectif fut de généraliser les propriétés métriques et différentielles des surfaces "usuelles" de l'espace euclidien à des espaces "courbés" considérés comme espaces de référence et non plus comme plongés dans un espace plus vaste de dimension supérieure : on parle de variétés. L'apport de la topologie introduite en ce domaine au tout début du 20è siècle, notamment avec Poincaré, permettra de développer, tout particulièrement avec l'américain Marston Morse, une théorie novatrice des variétés différentielles topologiques dont les applications touchent à la structure de l'univers (physique des particules, théorie des cordes).
i Marston Harold Calvin Morse : mathématicien américain (1892-1977) qui étudia à Harvard et obtint son doctorat (1917) portant sur les courbes géodésiques des surfaces à courbure négative, dirigé par George D. Birkhoff. Dans les années 1930, Morse développe la théorie portant aujourd'hui son nom relative à la nature de la topologie d'une variété différentielle par l'étude des géodésiques et lignes de niveau de fonctions définies sur cette dernière. On pourra consulter les références 7 & 8 in fine.
Une courbe plane ou gauche est une variété de dimension 1.
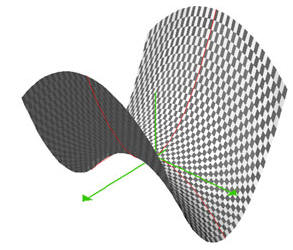
La sphère ou le paraboloïde hyperbolique (en forme de selle de cheval, ci-dessous) sont des variétés de dimension 2.
La notion de variété est très... variée. De façon élémentaire, dans le plan, une conique, un cercle sont des variétés de dimension 1. Dans l'espace euclidien de dimension 3 la sphère est une variété de dimension 2 (surface). Ces variétés admettent une équation polynomiale du type f(x,y,z,...) = 0. Ce sont des cas simples et concrets de variétés algébriques.
On pourra consulter la page consacrée à Claude Chevalley, et les références 5 & 6 in fine, pour une définition précise dans le cadre plus général la géométrie algébrique. On y rencontre les variétés algébriques affines, synonymes chez certains mathématiciens d'ensembles algébriques : K désignant un corps et n un entier naturel non nul, ce sont les points de Kn définis par un système d'équations polynomiales à coefficients dans K.
Élémentairement, en dimension 2 et 3, ces entités correspondent à des sous-espaces d'un espace affine (droites, plans) définis par un système d'équations de degré 1 en x, y, z, ... Par exemple, dans l'espace usuel de dimension 3, identifié à R3, une droite est définie par l'intersection de deux plans (affines), donc par un système de deux équations du type ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0. Le qualificatif d'affine, rappelant les espaces affines associés à un espace vectoriel, prend là tout son sens dans ce cas car si d = d' = 0, on retrouve les plans vectoriels qui les dirigent. Rappelons ici qu'un hyperplan est, dans Kn, une variété affine de dimension n-1.
Courbes gauches : » Surfaces algébriques : » Concept général de dimension : »
Les variétés topologiques :
On définit aujourd'hui abstraitement une variété topologique V de dimension n comme un espace topologique connexe séparé localement homéomorphe (homéomorphisme = bijection continue ainsi que sa réciproque) à un ouvert de Rn : chaque point de V admet un voisinage ouvert homéomorphe à un ouvert de Rn. On parle de variété topologique de dimension n. Lorsque n = 3, le très important et vaste sujet des variétés de dimension 2 est l'étude des surfaces, comme la sphère.
➔ Par exemple, à vue de nez, sur Terre, en chaque point de sa surface S, votre voisinage est homéomorphe localement à une "boule" de R2, en l'occurrence un disque (dimension 2), c'est à dire quelque chose de plat. Ce disque est pour vous une carte (locale) en x. Si l'ensemble de vos cartes recouvre S, elles constituent un atlas dont l'étude permet de rendre compte des propriétés de la variété.
! Si une variété est étudiée en tant que sous-espace ("plongée" dans un espace qui la contient), elle peut être limitée et posséder des points frontières qui vont en constituer le bord et la définition donnée au départ selon laquelle chaque point de V admet un voisinage ouvert homéomorphe à un ouvert de Rn ne convient alors plus car tout voisinage d'un point frontière déborde dans l'espace environnant. On convient alors de distinguer trois types de variétés topologiques :
les variétés closes : compactes, au sens topologique de fermées et bornées, et connexes.
La sphère, le tore, la bouteille de Klein sont des variétés closes de dimension 2 (surfaces). Elles n'ont pas de bord ou "d'extrémité". La définition donnée convient.
les variétés ouvertes : entrent dans cette catégorie les variétés non compactes, comme certains ouverts de Rn.
Par exemple, dans R : l'intervalle ]-1,1[ de dimension 1, dans R2 : le disque x²+y² < 1 de dimension 2, dans R3 : la boule unité ouverte x² + y² +z² <1, de dimension 3. Une telle variété n'a pas de bord au sens mathématique. La définition donnée convient là encore.
les variétés à bord : le bord (ou frontière) d'une variété fermée (au sens topologique) est l'ensemble de ses points frontières également dits points bordants. Comme dit ci-dessus, on les caractérise par le fait que tout voisinage d'un point frontière déborde dans l'espace environnant contrairement aux variétés closes où tout voisinage de tout point y est entièrement inclus.
Dans l'espace R3, le ruban de Möbius est une variété à bord. La boule unité x²+y²+z² ≤ 1 est une variété à bord : c'est la sphère unité d'équation x²+y²+z² = 1, surface close de dimension 2.

Dans le plan R2, le bord du disque fermé x²+y² ≤ 1 est le cercle unité, noté S1, de dimension 1. Dans R, le bord de l'intervalle fermé [-1,1] est la paire {-1,1} de dimension 0. » Théorème de Brouwer.
On peut définir formellement une variété à bord :
Une variété à bord est un sous-espace topologique de Rn dont les points admettent au moins un voisinage homéomorphe à Rn (point intérieur) ou bien un voisinage homéomorphe à un ouvert de Rn × R+, ensemble des points de Rn dont la n-ème coordonnée est positive (point bordant). L'ensemble des points n'admettant que ce dernier type de voisinage constitue le bord de la variété.
Dans le cas des surfaces (dimension 2) de l'espace euclidien 3D, tout point d'une surface à bord admet un voisinage homéomorphe à un ouvert de R × R+, c'est à dire à un demi-plan.
! Dans l'espace tous les points d'un disque sont des points frontières : il ne possède aucun point intérieur ! On voit là que le référentiel est fondamental pour extraire correctement des propriétés.
➔ D'une façon générale le bord (s'il existe) d'une variété de dimension n est une variété de dimension n-1.
La sphère Sn et la boule Bn:
Dans l'espace euclidien Rn, il est usuel de noter Sn-1(r) l'ensemble des points x de Rn+1 tels que || x || = r, sphère de centre O de rayon r. La sphère Sn-1(r) est le bord de la boule Bn(r) des points x de Rn tels que || x || ≤ r, r > 0, variété de dimension 3.
En dimension 3, la sphère usuelle est une variété de dimension 2.
Théorème d'homéomorphisme de Brouwer : » » Bonnet , Nash
Revenons à nos cartes locales : en formalisant, une carte locale apparaît comme étant, pour chaque x de V, le couple (Vx,hx) où hx désigne l'homéomorphisme associant au voisinage Vx (ouvert) de x, dit domaine de la carte, l'ouvert Ux de Rn de notre définition. La famille de cartes (Vx,hx) est un atlas de V.
Variétés différentielles :
Les "bonnes" variétés sont les variétés différentielles (ou différentiables) également dites lisses (smooth manifold en anglais, » ci-après), munies de difféomorphismes (homéomorphismes différentiables) et sur lesquelles on peut définir des coordonnées :
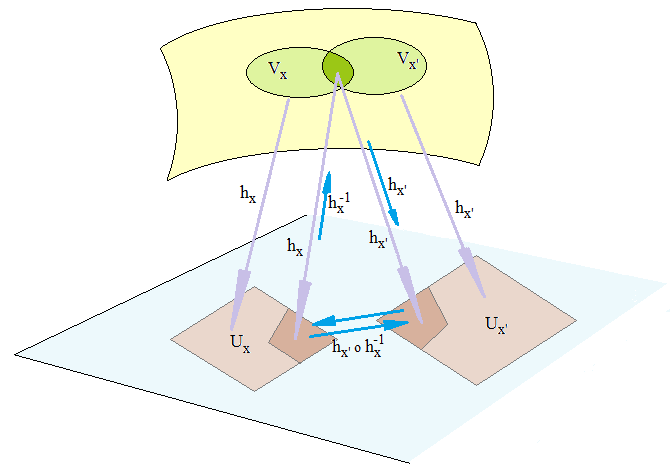
Supposons pour simplifier que n = 2 et considérons le schéma ci-dessus : via hx-1, réciproque de hx, on peut attribuer à tout point M de Vx un couple de coordonnées issu des points de Ux de R2. Mais un problème se pose pour les points de Vx∩Vx' lorsque cette intersection est non vide : le couple de coordonnées ne sera pas unique (voir le schéma ci-dessus) : un autre couple de coordonnées sera issu de Uy : on parle de coordonnées locales, c'est à dire dépendantes de la carte utilisée.
Passage d'une carte à l'autre :
L'application hx' o hx-1 envoie hx(Vx∩Vx')⊂Ux sur hx'(Vx∩Vx')⊂Ux' (colorés en brun ci-dessus) et permet de passer d'une carte à l'autre. En identifiant un point de Ux à son couple de coordonnées (u1,u2), on obtient son image (u'1,u'2) = hx' o hx-1(u1,u2) dans Ux' fournissant les coordonnées de M relativement à la carte (Vx,hx').
Ce changement de variable, en quelque sorte, au moyen de l'homéomorphisme composé hx' o hx-1, doit pouvoir se faire de façon optimale. On dit que deux cartes (Vx,hx) et (Vx',hx') sont compatibles si les deux homéomorphismes de changement de cartes hx' o hx-1 et hx o hx'-1 sont différentiables. Un atlas sera alors dit différentiable si les changements de carte le sont pour tous les Vx∩Vx' non vides.
Variété différentiable
de classe C![]() p:
p:
Une variété est dite
différentiable de classe C![]() p
pour exprimer qu'on peut lui associer un atlas différentiable dont les
changements de cartes sont de classe C
p
pour exprimer qu'on peut lui associer un atlas différentiable dont les
changements de cartes sont de classe C![]() p (p fois
continûment différentiables). Une variété analytique
est une variété de classe C∞, également qualifiée de
variété lisse (quoique certains auteurs
assimilent variété différentiable et variété lisse).
p (p fois
continûment différentiables). Une variété analytique
est une variété de classe C∞, également qualifiée de
variété lisse (quoique certains auteurs
assimilent variété différentiable et variété lisse).
Variété riemannienne :
Sur une variété, la distance euclidienne n'est généralement pas valable. Les géodésiques, minimisant les distances, ne sont généralement pas les segments de droite de la géométrie euclidienne. Il s'agit alors d'en définir une autre, intrinsèque (propre à la variété) ce qui peut être fort difficile si la variété est trop "tordue", les problèmes de rectification dans le plan étant déjà souvent ardus. Lorsque cela est possible, on parle d'espaces de Riemann, de variété riemannienne ou de géométrie riemannienne.
Plongement de Nash : »
Variété complexe :
➔ Si C remplace R, on parle de variété complexe. Les surfaces de Riemann, dont il est fait introduction ci-dessous, sont des variétés complexes de dimension 1. Elles s'identifient à des variétés différentiables de dimension 2 si l'on identifie C à R2. La généralisation de ces concepts à des dimensions supérieures conduit à la topologie différentielle et à la géométrie algébrique, branches très actives des mathématiques actuelles.
Sphère de Riemann : » Topologie, homéomorphisme : » » Veblen , Kodaira
| Fonctions multiformes, surfaces de Riemann : |
Afin de donner un sens aux fonctions multiformes à valeurs complexes (un point peut posséder plusieurs images), Riemann conçoit la notion appelée de nos jours surface de Riemann. Sur une telle "surface", constituée de "feuillets" raccordés continûment, une fonction multiforme devient uniforme (un point n'a qu'une seule image). Le calcul différentiel et intégral complexe, initié auparavant et principalement par Cauchy, peut s'y définir :
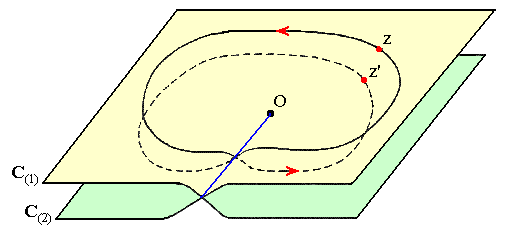
En savoir un peu plus sur les fonctions multiformes et les surfaces de Riemann : »
Ces travaux en géométrie différentielle conduisent ainsi Riemann à s'intéresser (1867) au célèbre 5ème et controversé postulat d'Euclide (postulat des parallèles) et à développer une géométrie non euclidienne en remplaçant ledit postulat par l'impossibilité de mener par un point une parallèle à une droite donnée !

On n'aboutit ainsi à aucune contradiction et une concrétisation de cette géométrie est celle de la sphère, surface à courbure constante positive, où les "droites" (géodésiques : trajectoires de cheminement minimum entre deux points) sont les grands cercles de la sphère : ceux dont le centre est celui de la sphère.
Ci-contre les "droites" rouge et bleu sont perpendiculaires à la "droite" équatoriale noire. Elles ne sont pas parallèles : elles se coupent en S et S'...
Notions sur les géométries non euclidiennes : »
➔ Pour en savoir plus :
Gesammelte Mathematische Werke (extraits en allemand des Oeuvres complètes) : http://www.emis.de/classics/Riemann/
Gesammelte Mathematische Werke (fonctions Abéliennes,
Riemann expose son idée de
feuillets) :
http://www.emis.de/classics/Riemann/AbelFn.pdf, page 56.
Introduction à la géométrie algébrique, (ensembles algébriques, variétés algébriques, topologie
de Zariski) par Rafael Guglielmetti,
École polytechnique de Lausanne :
http://rgug.ch/medias/math/geometrie_algebrique.pdf.