
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
 Les
célèbres coniques (ellipse, parabole, hyperbole)
étudiées par les mathématiciens grecs de
l'antiquité (Apollonis
de Perge,
Menechme,
Pappus)
peuvent être définies au moyen d'un point appelé
foyer
(Kepler)
et d'une droite (d) dite
directrice
(Pappus).
Les
célèbres coniques (ellipse, parabole, hyperbole)
étudiées par les mathématiciens grecs de
l'antiquité (Apollonis
de Perge,
Menechme,
Pappus)
peuvent être définies au moyen d'un point appelé
foyer
(Kepler)
et d'une droite (d) dite
directrice
(Pappus).
Ainsi, une conique est l'ensemble des points M tels que MF/MH = e où H désigne la projection orthogonale de M sur (d) et e un nombre strictement positif donné. Ce nombre e est appelé excentricité de la conique.
La perpendiculaire à (d) passant par F est l'axe focal : il s'agit là de la droite (KF), K désignant la projection orthogonale de F sur (d).
Cette définition permet d'affirmer que (FK) est un axe de symétrie de la conique. Le point S de (FK) vérifiant SF/SK = e est le sommet de la conique. Lorsque e est distinct de 1, il existe deux points S et S' divisant [KF] dans le rapport e : c'est dire que la conique admet un second sommet S'.
Ci-dessus : le cas relativement simple de la parabole, obtenu lorsque e = 1. La tangente en M à la parabole est la médiatrice de [FH].

Équation cartésienne, équation réduite :
 Dans un repère
orthonormé d'origine F, l'axe des abscisses étant dirigé par le vecteur
KF, en élevant au carré, la relation MF/MH = e se traduit par
:
Dans un repère
orthonormé d'origine F, l'axe des abscisses étant dirigé par le vecteur
KF, en élevant au carré, la relation MF/MH = e se traduit par
:
x2 + y2 = e2(k - x)2 (1)
où k désigne l'abscisse (négative) de K relativement à F.
Si nous faisons y = 0, il vient x = ± e(k - x) : il s'agit des deux sommets S et S' auxquels il était fait ci-dessus allusion, à condition que e soit distinct de 1 :
xS = ek/(e + 1) , xS' = ek/(e - 1)
♦ Si e = 1, cas de la parabole, l'unique sommet S vérifiant xS = k/2 est le milieu de [KF].
♦ Si e ≠ 1, choisissons maintenant le milieu Ω de [SS'], donc d'abscisse ω = ke2/(e2 - 1) relativement à F, comme nouvelle origine. L'équation (1) ci-dessus, comme on le constate par le calcul en posant X = x - ω, Y = y, ne possède pas de coefficient en X. En posant ε = e2 - 1, donc ω = ke2/ε, on obtient :
(X + ω)2 + Y2 = e2(k - X - ω)2 = e2(X + k/ε)2
En développant et simplifiant :
X2
+
ω2
+ 2ωX
+ Y2
= e2X2
+ e2k2/ε2
+ 2kXe2/ε
Finalement :
X2ε - Y2 = e2k2/ε (2)
➔ Dans ce cas e ≠ 1, la conique admet donc Ω comme centre de symétrie (X → -X et Y → -Y laissent l'équation invariante). Cette symétrie prouve l'existence d'un second foyer F' symétrique de F par rapport à Ω.
Une conique à centre (ellipse, hyperbole) est donc une courbe algébrique de degré 2 admettant non seulement l'axe focal (l'axe des X potant F et F') comme axe de symétrie mais aussi la perpendiculaire à cet axe passant par son centre Ω, appelé axe transverse (l'axe des Y), ce dernier étant le second axe de symétrie la courbe.
∗∗∗
On se donne une unité, un
droite (d), un foyer F avec FK = 3, l'excentricité e = 1/2.
Dans le repère (ΩX,ΩY),
Vérifier que l'on obtient dans ces conditions
: X2/4 + Y2/3 = 1, ellipse représentée ci-dessous.
Cas de l'ellipse et de l'hyperbole :
i/ En divisant par e2k2/ε, l'équation (2) ci-dessus prend les formes suivantes, dites réduites :
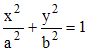 (ellipse,
e < 1) ou bien
:
(ellipse,
e < 1) ou bien
:  (hyperbole,
e > 1)
(hyperbole,
e > 1)ii/ En notant F'(-c,0) et F(c,0) les foyers, on montre alors aisément que :
si a > b, a2 - b2 = c2, cas de l'ellipse;
si a < b, a2 + b2 = c2, cas de l'hyperbole;
l'excentricité est e = c/a (appliquer la relation initiale MF/MH = e au cas particulier d'un sommet).

iii/ Droites remarquables :
La droite (FF') est baptisé axe focal.
La droite perpendiculaire à l'axe focal passant par le centre de la conique est l'axe transverse.
Les directrices ont pour équations x = ± a2/c.
L'hyperbole possède deux asymptotes passant par son centre d'équations respectives ay = ± bx. Elle est dite équilatère si a = b. Le centre est alors centre de symétrie de la courbe.
➔ Dans le cas de l'ellipse, le cas a = b s'interprète comme un cercle de centre Ω, de rayon a. Lorsque a > b, a est dit demi grand axe, b est le demi petit axe. Si a < b, on échange le rôle de x et de y, ce qui revient à faire une symétrie orthogonale par rapport à la 1ère bissectrice du repère. Les foyers sont alors portés par l'axe des ordonnées du repère (Ω,X,Y).

Dans le cas de l'hyperbole l'échange des rôles de x et de y conduit à une hyperbole dont les foyers seront également portés par l'axe des ordonnées :
➔ La définition par foyer et directrice permet de retrouver les relations fondamentales de la définition bifocale :
MF + MF' = 2a (» ellipse) | MF' - MF | = 2a (» hyperbole)
En effet, dans le cas de l'ellipse, on a :
MF = eMH et MF' = eMH', donc MF + MF' = e(MH + MH') = e × 2a2/c
Or e = c/a, d'où le résultat. Le cas de l'hyperbole s'obtient de la même manière en remarquant que les directrices coupent l'axe focal entre S et S' (puisque e = c/a > 1).
L'ellipse du jardinier :
La définition bifocale de l'ellipse) est utilisée par les jardiniers pour fabriquer de beaux massifs elliptiques : il suffit d'une corde tendue entre deux piquets (les foyers) au moyen d'un troisième qui décrira l'ellipse. L'ensemble de tels points fut étudié géométriquement (indépendamment de l'aspect analytique décrit ci-dessus) par La Hire au 17è siècle.
Résumé des principales caractéristiques de l'ellipse et de l'hyperbole (équations réduites) :
|
Ellipse x2/a2 + y2/b2 = 1
Abscisses foyer : Excentricité : e = c/a Directrices : x = ± a2/c (a > b) , x = ± b2/c (a < b) Tangentes en M(xo,yo) : xxo/a2 + yyo/b2 = 1 |
Hyperbole x2/a2 - y2/b2 = ε (±1) Abscisses foyer : c2 = a2 + b2 Excentricité : e = c/a (ε =1) , e = c/b (ε = -1) Directrices : x = ± a2/c (ε =1) , y = ± b2/c (ε= -1) Asymptotes : ay = ± bx Tangentes en M(xo,yo) : xxo/a2 - yyo/b2 = ±1 |
Étude des tangentes (ellipse, hyperbole, tangente) : »
∗∗∗
Dans le cas de l'ellipse ci-dessus, d'équation X2/4 + Y2/3 = 1,
on a : a = 2, b =
3, c2 = b2 - a2, donc c =
√5.
Les
directrices ont pour équation y = ± b2/c
= ± 9/√5.
∗∗∗
On a tracé ci-dessous une hyperbole de
foyers F et F', de directrices (d) et (d').
a) Calculer son équation réduite. Rép
: x2/4
- y2/12 = 1. Préciser la valeur de a.
b) Vérifier sur cet exemple que MF' - MF = 2a pour tout M de la branche passant
par S.

Ovales de Descartes : »
∗∗∗

Cas de la parabole :

y2 = 2px
Soit K la projection orthogonale du foyer F sur la directrice (d). Pour tout point M de la parabole, on a MF = MH. Traçons [KF) : c'est (manifestement) l'axe de symétrie de la parabole.
Notons S le milieu de [KF], sommet de la parabole, SF = SK et posons p = KF > 0. On a M(x,y), F(p/2,0) et (d) : x = -p/2. L'égalité MF2 = MH2 conduit immédiatement à y2 = 2px. Inversement, dans un repère orthonormé d'origine O, toute équation de la forme y2 = 2px ou x2 = 2py (p > 0) est une parabole de sommet O.
» Si les rôles de x et de y doivent être échangés (cas d'un axe "vertical") l'équation ci-dessus se ramène à x2 = 2py
Le nombre positif p est le paramètre de la parabole. Vu que MF/MH = 1 pour tout point de la parabole, on remarquera que l'on retrouve p dans le cas particulier d'un point M se projetant orthogonalement en F.
| Équation en coordonnées polaires : |


On obtiendra facilement ce résultat en posant KF = p/e, ^(Fx,FM) = t, r = FM et en remarquant que :
KF = Km + mF = HM - r × cost
p > 0 est le paramètre de la conique;
e est son excentricité : parabole (e = 1), ellipse (e < 1), hyperbole (e > 1).
Dans le cas particulier où M se projette orthogonalement en F, vu que MF/MH = e, on aura alors MF/MH = MF/KF = e, donc MF = eKF = p : comme pour la parabole, le paramètre p est la longueur de la demi-corde passant par un foyer et perpendiculaire à l'axe focal (la corde mesure donc 2p).
➔ Prendre le foyer comme pôle semble logique eu égard à l'aspect cosmologique : le Soleil, centre de notre système local. Mais on peut préférer le centre de l'ellipse, compte tenu de la symétrie : dans ce cas, en posant x = r.cos t , y = r.sin t, t∈[0,2π], on élève au carré et on reporte dans l'équation réduite x2/a2 + y2/b2 = 1. Vu que c2 = a2 - b2 (b < a, sinon on échange a et b), on obtient très facilement :
r2 = a2b2/(a2 - c2cos2t)
ou bien en faisant intervenir l'excentricité e = c/a < 1 :
r2 = b2/(1 - e2cos2t)
Pour un tracé, on pourra se contenter de prendre la détermination positive de la racine carrée. En effet, compte tenu de la symétrie par rapport à O, un point M(r,t) se retrouve en M(-r,t) = M(r,t + π). On obtiendra facilement un résultat analogue pour l'hyperbole en partant de l'équation x2/a2 - y2/b2 = 1 conduisant à : r2 = b2/(e2cos 2t - 1)
Dans la recherche de l'équation polaire, partir de l'équation paramétrée x = f(t), y = g(t) et élever au carré pour obtenir x2 + y2 égalisé à r2
∗∗∗
Où l'on retrouve l'équation polaire de l'ellipse :
i/
Avec les notations usuelles MF + MF' = 2a de la définition bifocale, on
pose MF = r.
Prouver que : MF'2 = r2
+ 4c2 - 4rc.cos t.
ii/
Déduire de MF + MF' = 2a que r = b2/(a - c.cos
t).
iii/ On pose p = b2/a. Retrouver l'équation
polaire r = p/(1 - e.cost) (b < a) et
p = e × KF.
☼

∗∗∗
On se donne une unité, un droite (d), un foyer F avec FK = 3, l'excentricité e =
1/2.
Vérifier dans ces conditions que p = 3/2 puis que r = 3/(2 - cost). Les sommets
de l'ellipse sont obtenus pour t = 0 et t =
π, d'où
S(3,0) et S'(1,π).
En déduire le grand axe. Lorsque t = ±π/2,
on obtient r = 3/2 : logique, la distance entre ces points est 2p = 3.
Placer les points correspondant à t = π/6
et t = π/3 et
justifier qu'on obtient pour cette valeur un des sommets B de l'ellipse.
En déduire l'expression de l'équation réduite.

➔ Le changement de r en - r conduit au symétrique de la conique par rapport à F. Le changement de t en π + t conduit au symétrique de la conique par rapport à l'axe polaire π/2 (» coordonnées polaires). C'est dire que les équations :
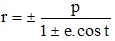
correspondent à des coniques isométriques. » complément dans le cas de l'ellipse » Kepler
Comparativement aux équations réduites de l'ellipse et de l'hyperbole, on a : p = b2/a et e = c/a. Ces formes polaires fournissent une interprétation du cercle comme conique particulière dite dégénérée : e = 0, cercle de centre F, de rayon p.

➔ Dans le cas de l'ellipse et de l'hyperbole, on peut aussi prendre le centre comme pôle : pour le calcul, on pourra se reporter au cas de l'ellipse, le cas de l'hyperbole étant semblable au signe près.
L'hyperbole admet deux droites asymptotes (du grec sumptôsis = rencontre) : pour x et y infinis, l'hyperbole se confond avec ces droites. Eu égard à l'équation réduite, leurs équations sont :
y = (-b/a)x et y = (b/a)x
Rapportée à ses asymptotes, c'est à dire prises comme axes du repère, l'équation de l'hyperbole prend la forme simple, dite homographique :
| Équations d'une conique (autre que le cercle) rapportée à un sommet : |
On a vu ci-dessus, qu'en prenant comme origine le sommet de la parabole et pour axe des abscisses l'axe focal, l'équation de la courbe est de la forme y2 = 2px. On peut obtenir un résultat analogue pour l'ellipse et l'hyperbole à partir de l'équation cartésienne réduite, à savoir, p désignant le paramètre :
y2 = 2px + (e2 - 1)x2
Le cas de la parabole se retrouve puisqu'alors e = 1.
Pour l'ellipse,
e = c/a < 1, vu que p = b2/a, e = c/a
et a2 = b2 + c2, on
peut aussi écrire :
y2 = 2px
- b2x2/a2
= 2px - px2/a = 2px - (1 - e2)x2
Pour l'hyperbole,
e = c/a > 1, vu que p = b2/a, e = c/a
et a2 + b2 = c2
:
y2 = 2px
+ b2x2/a2
= 2px + px2/a, 2px + (1 - e2)x2
Afin d'établir ces équations, il suffit de faire le changement de variable menant le centre Ω en S(-a,0), donc de poser X = x + a et Y = y dans l'équation réduite x2/a2 ± y2/b2 = 1.
i
On
comprend ainsi pourquoi
Desargues,
qui est à l'origine de la géométrie projective et étudia
donc les coniques avec précision, appela
défaillement l'ellipse, directement tiré du mot greco-latin d'Apollonius
: ellipsis = déficient car on retire px2/a.
La
parabole
était baptisée égalation (on ne retire rien !) et l'hyperbole
était dite outrepassement
: car on ajoute px2/a.
| Équations paramétriques des coniques à centre (ellipse, hyperbole) : |
Les coniques à centre ont aussi une représentation paramétrique pratique que l'on peut obtenir au vu de l'équation réduite x2/a2 + y2/b2 = 1 (cas de l'ellipse) et x2/a2 + y2/b2 = 1 (cas de l'hyperbole) :
Ellipse :
x = a.cos t , y = b.sin t, t décrivant [0,2π]
Le paramètre t est l'anomalie excentrique (le terme est de Kepler). En posant u = tan(t/2), on obtient une paramétrisation rationnelle :
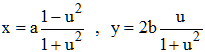

Ellipse : x = 4cos t , y = 3sin t
Hyperbole :
x = a/cos t , y = b.tan t , t décrivant [0,π].
En posant u = tan(t/2), on obtient une paramétrisation rationnelle :
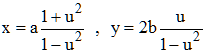

hyperbole équilatère x2 - y2 = 1
ou encore : x = 1/cos
t , y = tan
t, les asymptotes sont en
bleu : y
= ± x
∗∗∗
Soit x2/a2 - y2/b2
= 1, l'équation d'une hyperbole (son axe focal est donc x'x).
i/ Justifier que l'on peut poser y = b.tan t, t décrivant
]o,+π[
ii/ En déduire x = ± a/cos t, t
décrivant ]o,+π[.
iii/ Déduire des variations de cos t, celle de 1/cos
t (on fera un simple tableau de variation) et conclure que l'on peut
se contenter de la détermination
x = + a.cos t. d'où
l'équation paramétrique de l'hyperbole : x = a/cos t , y = b.tan
t, t décrivant ]o,+π[.
| Équation de la tangente à une conique en un point : |
L'équation de la tangente en un point Mo(xo,yo) d'une courbe f(x,y) = 0 est donnée par :
y - yo = y'o(x - xo)
• Cas de l'ellipse x2/a2 + y2/b2 = 1 : on a, en dérivant par rapport à x , la relation 2x/a2 + 2yy'/b2 = 0, c'est dire que y'o = -b2/a2 × xo/yo. en reportant dans l'équation de la tangente, on est conduit immédiatement à cette formule facilement mémorisable, dite du dédoublement des variables, principe également valable pour l'hyperbole et la parabole :

Lorsque l'ellipse est définie paramétriquement, on obtient les équations u = tan(t/2) :

Propriétés géométriques de la tangente à l'ellipse : »
• Cas de l'hyperbole x2/a2 - y2/b2 = 1 : un calcul rigoureusement analogue fournit :

Lorsque l'hyperbole est définie paramétriquement, on obtient les équations :

Propriétés géométriques de la tangente à l'hyperbole : »
• Cas de la parabole y2 = 2px : on vérifiera aisément que la tangente en Mo(xo,yo) a pour équation

Théorèmes de Poncelet :
»
∗∗∗
Tangentes perpendiculaires &
cercle orthoptique de Monge
➔ Une intéressante concrétisation des sections coniques est le travail d'un artisan espagnol, tourneur sur bois et du réalisateur espagnol Alejandro Amenábar pour le film Agora : » Hypatie d'Alexandrie.