ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 MOIVRE Abraham
de-,
anglais, 1667-1754 |
Français
d'origine, né à Vitry-le-François, fils d'un médecin protestant (huguenot), Abraham de Moivre,
s'intéresse dès l'enfance à l'algèbre et à l'arithmétique. Il étudie à
l'académie protestante de Sedan jusqu'à sa fermeture en 1681. Étudiant les
mathématiques et la physique à Paris auprès d'Ozanam,
de Moivre subit les persécutions à l'encontre des protestants lors de la
révocation de l'Édit de Nantes (1685). Emprisonné, il est libéré en 1688 et
quitte la France pour l'Angleterre.
A Londres, il donne des cours privés sans obtenir de poste universitaire. Cependant introduit par Newton et l'astronome Edmond Halley devenu son ami, il fit son entrée à la Royal society en 1697. Ce n'est que quelques mois avant sa mort, à l'âge de 87 ans, longévité rare pour l'époque, que l'Académie des sciences de Paris lui ouvrit ses portes en tant que membre étranger (n'oublions pas qu'il était français d'origine...).
Suite aux travaux entamés par Jakob Bernoulli dans son Ars Conjectandi, de Moivre apporta une très importante contribution au calcul des probabilités, à cette époque branche nouvelle des mathématiques, avec la publication de De mensura sortis (De la mesure du hasard, 1711) puis de The Doctrine of Chances (La théorie des chances, 1718) qu'il dédia à Newton. De Moivre fut un ami de James Stirling.
➔ Ce terme de chance (= hasard, possibilité en anglais), utilisé en France, avec, entre autres, Pascal et Fermat, rappelle que le calcul des probabilités trouve son origine dans les jeux de hasard ce dernier mot provenant de l'arabe ez zahr = dé à jouer signifiant également chance. On remarque que l'intitulé entier est complété par A method of calculating the probabilities of events in play (soit Une méthode de calcul des probabilités des événements au jeu). Déjà utilisé en latin (probabilitas) dans son De mensura sortis (1711), il semble qu'Abraham de Moivre fut le premier à utilisé le terme probabilité en mathématiques.
| La formule des probabilités composées (1718) : |
Dans
son traité de 1718, Abraham de Moivre définit l'indépendance en probabilités et
énonce la règle selon laquelle deux événements sont indépendants lorsque
la probabilité de leur réalisation conjointe est égale au produit des
probabilités de réalisation de chacun. En termes actuels :
Prob (A∩B) = Prob(A) × Prob(B)
Ce qui se généralise à n événements :
Prob (A1∩A2∩...∩An) = Prob(A1) × Prob(A2)... × Prob(An)
» Depuis Kolmogorov, avec l'introduction du langage des ensembles dans le calcul des probabilités, la probabilité Prob(A et B) de la conjonction de A et B peut se noter Prob(A ∩ B).
Et on lui doit la célèbre formule dites des probabilités composées bien connue aujourd'hui des lycéens :
Prob(A∩B) = Prob(A) × Prob(B/A) = Prob(B) × Prob(A/B)
où Prob(A/B) désigne la probabilité de réalisation A sachant que B est réalisé : probabilité conditionnelle de A par rapport à B. Formule qui sera complétée par Thomas Bayes une quarantaine d'années plus tard avec celle des probabilités des causes.
Lorsque P(A/B) = P(A), alors P(B/A) = P(B) et ont dit que les événements A et B sont indépendants en probabilité et Prob(A∩B) = Prob(A) × Prob(B).
| Formule de Moivre-Stirling : |
On doit aussi à Abraham de Moivre la formule dite aujourd'hui de Stirling avec lequel il correspondit dans les années 1730, donnant pour n grand, une approximation de la factorielle de n, nombre noté n! (notation due à Christiant Kramp) égal au produit n premiers entiers naturels :
n! = 1 × 2 × 3 × ... × n
Étude de la formule, usage du tableur : »
| Loi binomiale et tendance vers une loi normale, théorème de Moivre-Laplace : |
Rappelons qu'une distribution binomiale est engendrée par la somme de n variables aléatoires indépendantes de Bernoulli B = X1+ X2 + ... + Xn , les Xi ne pouvant donc prendre que deux valeurs : 1 avec la probabilité p et 0 avec la probabilité q = 1 - p. On a, pour tout k ≤ n :
Cnk désignant le nombre de combinaisons de k objets parmi n. L'espérance mathématique de B est np, son écart-type est σ = √(npq).
En 1730, de Moivre publie Miscellanea Ananlytica de seriebus et quadraturi, un traité mêlant l'étude des séries, du calcul intégral et des probabilités et, faisant usage de la formule de Stirling, sera le premier à découvrir la possibilité d'approcher une loi binomiale B(n,p) par la loi normale en constatant que lorsque n tend vers l'infini, la variable centrée réduite de B, à savoir :
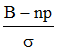
tend vers une loi continue (convergence en loi) dont la densité est :
IL s'agit de la loi centrée réduite de Laplace-Gauss, également dite loi normale. Ce résultat est un cas particulier d'un très important théorème : le théorème central limite, parfois aussi appelé de Moivre-Laplace.
Théorème central limite, convergence en loi : » Loi binomiale et approximation par la loi normale : »
➔ Lorsque n est grand et p non voisin de 0 et 1, B peut être loi normale N(np,σ) où σ est l'écart-type de la loi B, racine carrée de la variance, à savoir σ = √(npq). On constate au moyen de tables que l'approximation est acceptable lorsque sont réunies les trois conditions :
| La formule de Moivre (ou de de Moivre) : |
Algébriquement, l'ensemble C des nombres complexes est un corps commutatif. Tout nombre complexe z peut donc, a priori, être élevé à une puissance entière, réelle, voire complexe.
Concernant les puissances entières, la paternité de cette célèbre formule (1722), dont les mathématiciens suisses Lambert et Euler feront grand usage, revient sans doute à Cotes (mort prématurément à 34 ans en 1716). Pour tout t réel et n entier :
La notation i remplace √-1 utilisée par de Moivre.
➔ La formule de Moivre s'obtient aisément par récurrence sur n dans l'ensemble des entiers naturels. Mais la formule reste vraie pour un entier négatif : soit n un entier relatif négatif; posons m = - n > 0 :
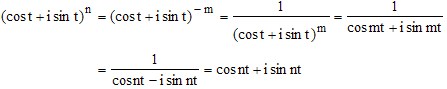
La dernière égalité est due au fait que si z est un nombre complexe de module 1, on a zz = 1, donc 1/z = z.
! La formule ne s'applique pas à des valeurs rationnelles non entières de n !
Un tel nombre n = m/p conduirait formellement à :
(cos t - i.sin t)n = (cos t - i.sin t)m/p = [(cos t - i.sin t)m]1/p = (cos mt - i.sin mt)1/p
et cette dernière écriture est illicite car elle tend à exprimer la racine p-ème du nombre complexe cos mt - i.sin mt et on sait qu'un tel nombre n'est pas unique : d'une façon générale, dans l'ensemble C des nombres complexes, écrire z = am/p n'a généralement pas de sens.
Dans le cas simple de n = 1/3 et a complexe donné l'écriture z = a1/3 conduirait à rechercher z complexe tel que z3 = a. Le cas de a = 1 est édifiant et conduit facilement à trois solutions : les racines cubiques de l'unité, à savoir 1, j = (-1 + i√3)/2 et (-1 - i√3)/2 = j2. On a 1 + j + j2 = 0.
Racines n-èmes dans C, racines n-èmes de l'unité : » Puissance d'un nombre dans R ou C : »
| Linéarisation de polynômes trigonométriques : |
La célèbre formule permet des calculs aisés sur les nombres complexes écrit sous forme trigonométrique z = r(cos t + i.sin t) et, en particulier, de linéariser des polynômes trigonométriques, technique chère aux élèves des Terminales scientifiques des lycées, ayant généralement pour objectif un calcul de primitive.
En changeant t en -t, on a (cos t - i.sin t)n = cos nt - i.sin nt; par suite, en utilisant la notation d'Euler, cos t + i.sin t = eit, on a :
Exemples : linéarisons sin3t. On a :
Et on établirait facilement de même : cos3 t = ¼(cos3t + 3cost). On a également :
sin4 t = (cos4t - 4cos2t + 3)/8 et cos4 t = (cos4t + 4cos2t + 3)/8
∗∗∗
a) Exprimer cos3t en fonction de
sin t et cos t puis en fonction de
cos t seul. En déduire la forme linéarisée de cos3t
b) linéariser sin3tcos4t.
☼
Autres exercices niveau Ter/Sup : »
| Autres contributions : |
On doit aussi à Abraham de Moivre :
Les premiers résultats sur la décomposition des fonctions rationnelles (quotient de deux polynômes) en éléments simples afin de calculer leurs primitives
Une théorie des fonctions hyperboliques dont il est, avec Lambert, le promoteur.
Les premières études sur le difficile problème de la résolution par radicaux des équations polynomiales de degré impair en les ramenant au degré n par un subtil calcul basé sur le changement d'inconnu X = x + 1/x. Sur ce sujet, on pourra consulter le lien 4 proposé in fine.
» Vandermonde , Abel , Galois Polynômes réciproques, équations réciproques de degré pair : »
➔ Pour en savoir plus :
Le De mensura sortis (1711) d'Abraham de Moivre
(en latin) :
https://ia801904.us.archive.org/10/items/jstor-103118/103118.pdf
The Doctrine of Chances (3ème édition de 1756,
Londres) d'Abraham de Moivre (en anglais) :
https://ia801408.us.archive.org/6/items/doctrineofchance00moiv/doctrineofchance00moiv.pdf
Miscellanea Ananlytica de seriebus et quadraturi (édition 1730,
Londres) d'Abraham de Moivre (en latin) :
https://archive.org/stream/bub_gb_TFX1165yEc4C#page/n3/mode/2up/search/Bernoulli
De la résolution algébrique de l'équation xp
- 1 = 0 lorsque p est premier, par M. Realis (Nouvelles Annales
mathématiques, 1843) :
https://books.google.fr/books?id=aQ0FAAAAQAAJ&pg=PA5&lpg=PA5&dq=xp -
1#v=onepage&q=xp - 1&f=false
Saccheri
»