ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 JACOBI
Karl Gustav Jacob,
allemand, 1804-1851 |
Fils
d'un banquier juif, après ses études à l'université de Berlin, il y obtint un
premier poste d'enseignement (1825) ayant dû, pour postuler, se convertir au
christianisme ! Jacobi sera nommé l'année suivante à l'université de
Königsberg
(1826),
où il sera l'ami de Bessel.
A Paris, il se liera avec les grands mathématiciens de l'époque comme Legendre et Poisson. Il reprit une chaire de mathématiques à Berlin en 1843 où il sera membre de la très réputée Académie des sciences.
Ses travaux portent essentiellement, indépendamment d'Abel à la même époque, sur l'étude des fonctions elliptiques (dès 1826 mais publié avec le soutien de Legendre en 1829 : Fundamenta nova theoriae functionem ellipticarum), les équations différentielles et aux dérivées partielles (pour lesquelles il préconisa la notation ∂ proposée par Legendre les systèmes d'équations linéaires, la théorie des déterminants, que développèrent Cauchy et Cayley.
Jacobi fut aussi un des principaux artisans du journal de Crelle. Un très grand nombre de résultats d'algèbre et d'analyse portent ou utilisent son nom.
Fourier avait reproché à Jacobi (et à Abel) de perdre leur temps dans leurs travaux sur les fonctions elliptiques alors que la physique attendait des outils mathématiques (thermodynamique en particulier). Jacobi répondit « qu'un philosophe comme lui devrait savoir que la seule fin de la science est l'honneur de l'esprit humain et, qu'à cet égard, une question concernant les nombres a autant de prix qu'une question sur le système du monde ».
| Jacobien d'une application de plusieurs variables (1829) et application au calcul intégral : |
Soit u une application différentiable sur un ouvert de Rn et à valeurs dans Rp. Notons X = (x1, x2, ..., xn) le n-uplet de ses variables (n ≥ 2) et notons u : X → (u1(X), u2(X), ...up(X)). Chaque ui est dérivable par rapport à chacune des variables x1, x2, ..., xn.
i La notation actuelle des dérivées partielles au moyen du "d rond" ∂, comme utilisée ci-dessous, n'apparaît avec Jacobi qu'en 1841 dans un article publié dans le Journal de Crelle. Mais son usage reste alors confidentiel. » Legendre.
Les ∂ui/∂xj désignant les dérivées partielles des ui par rapport à xj au point X = (x1, x2, ..., xn), la matrice jacobienne de u au point X est la matrice p × n définie par :
Restreignons-nous au cas de R2 dans R2. La matrice jacobienne de u au point X = (x1,x2) est la matrice 2 × 2 :
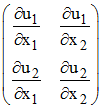(mj)et le jacobien de u en est le déterminant fonctionnel que l'on note J(u) ou, souvent, symboliquement :
Le jacobien trouve en particulier son emploi dans le calcul des intégrales multiples (généralisation du changement de variable dans les intégrales simples), en géométrie différentielle et dans la résolution des équations différentielles.
Exemple classique de changement de variables:
Dans le plan, on désire passer des coordonnées cartésiennes (x,y) aux coordonnées polaires (r,t) en posant x = r.cos
t et y = r.sin
Le jacobien J(u) est son déterminant, soit r.cos2t + r.sin2t = r.
➔ Supposons maintenant que f soit une fonction intégrable sur un domaine K de R2, le domaine d'intégration équivalent en r et t est u-1(K), image réciproque de K par f qui doit pouvoir être déterminé sans ambiguïté, ce qui exige u invective. Par conséquent la matrice jacobienne doit être inversible, ce qui revient à dire que son déterminant, le jacobien de u, est non nul. Dans le cas présent, cela signifie r non nul et on démontre que :
Dans le cas général d'un intégrale dans Rn, la formule de changement de variables s'écrit :
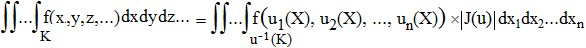
En application, on peut calculer l'intégrale dite de Gauss :
Calcul :
»Cas des coordonnées sphériques (dimension 3) :
Dans l'espace euclidien de dimension 3, on peut poser x = r × cos
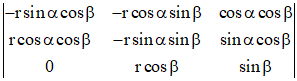
En développant suivant la 1ère colonne, J(u) =
r2cosβ.
!!
Suivant l'expression choisie des coordonnées
sphériques, le jacobien sera différent ! Il est par exemple tout à fait licite
de préférer x = r × cosα.sinβ, y = r × sinα.sinβ, z =
r × cosβ,
avec ici β ∈ [0,π], auquel cas J(u) = -r2sinβ.
Application au calcul du volume de la sphère : »
| Méthode itérative de Jacobi : |
Il s'agit d'une méthode de résolution des systèmes d'équations linéaires n × n. L'algorithme se prête bien au traitement sur ordinateur :
Étude de l'algorithme : » » Seidel
| Identité de Jacobi pour le produit vectoriel : |
Si u, v et w sont trois vecteurs de l'espace, alors :
u ∧ (v ∧ w) + v ∧ (w ∧ u) + w ∧ (u ∧ v) = 0
Preuve : utiliser la formule de Gibbs u ∧ (v ∧ w) = (u.w).v - (u.v).w ici présente sous forme d'exercice.
Gibbs et le produit vectoriel : » Lien avec les algèbres de Lie : »
| Identité (algébrique) de Jacobi : |
Utilisée par Jacobi en théorie additive des nombres, cette identité s'écrit :
3(x2 + y2 + z2) = (x + y + z)2 + 2(x/2 + y/2 - z)2 + 6(x/2 - y/2)2
On pourra la vérifier facilement en développant et réduisant le second membre.
Programmation du théorème des 3 carrés : »
| Fonctions théta (θ) de Jacobi (1828) : |
Les fonctions elliptiques, d'une variable complexe sont des fonctions méromorphes. Dans l'étude de ces fonctions et poursuivant des travaux initiés par Abel et Gauss, Jacobi définit les fonctions θ, séries entières d'exponentielles complexes permettant d'exprimer les fonctions elliptiques sn, cn et dn en tant que quotient de telles fonctions.
Les fonctions θ verront leur application dans le domaine arithmétique, où on ne les attendait pas vraiment... La théorie des fonctions elliptiques d'une variable complexe mène en effet à la recherche de l'existence de points à coordonnées rationnelles sur une courbe elliptique, aux fonctions modulaires, et à la preuve du grand théorème de Fermat.
Un théorème de Jacobi (Journal de Crelle, 1835) :
Une fonction méromorphe d'une variable complexe possède au
plus 2 périodes
et leur rapport est imaginaire (complexe, non réel).
La notion de fonction doublement périodique : »
➔ Pour en savoir plus :
Dirichlet
