Séries trigonométriques, séries de Fourier   » Analyse de Fourier (analyse harmonique) | Séries de Fourier d'une fonction de carré intégrable

Une série trigonométrique est une série de fonctions Σu_n(x) (à termes réels ou complexes) dont le terme général u_n(x) est de la forme :

u_n(x) = a_ncos(nx) + b_nsin(nx)

Les coefficients de Fourier d'une fonction f supposée 2π-périodique sont, pour tout n de N :

On peut bien entendu remplacer l'intervalle d'intégration [0,2π] par [-π,+π] où tout autre intervalle d'amplitude 2π. Les a_n (resp. b_n) sont nuls pour tout n si f est impaire (resp. paire). La série trigonométrique, dite de Fourier, associée à f est alors :

Cette série n'est hélas pas nécessairement convergente et si elle converge, elle ne converge pas nécessairement vers f(x) !

Comment justifier les coefficients parachutés ci-dessus et la présence bizarre de ce ao/2 ?

Si l'on désire développer en série trigonométrique une fonction 2π-périodique, son développement sera de la forme :

          (sf)

Multiplions les deux membres par cos nx et intégrons sur un intervalle J quelconque d'amplitude 2π. En Supposant la convergence uniforme, vœu du physicien, on peut intervertir les signes d'intégration et de sommation; or l'intégrale de cos nx.cos px est nulle et l'intégrale de cos²nx est égale à π. Finalement :

 ➔  D'où la formule fournissant a_n et la présence du a_o/2 dans le développement de Fourier : afin de préserver la formule générale des a_n, on traite à part le cas n = 0. Un calcul similaire, en multipliant par sin nx, permet de retrouver la formule des b_n (remarquer que b_o n'intervient pas). La sommation commence donc à n = 1.

Les sommes partielles S_n de la série  (sf) peuvent s'écrire au moyen de f :

 

Cas plus général d'une fonction T-périodique :

Si f est de période T, on peut procéder comme ci-dessus en posant, selon la tradition, T = 2π/ω. On obtiendra un développement de f de la forme :

Les coefficients a_n et b_n sont obtenus par :

L'intégration porte sur n'importe quel intervalle de longueur T. On peut préférer remplacer 2/T par π/ω qui lui est égal.

 ➔  le terme constant a_o/2 correspond à la valeur moyenne de la fonction f sur une période :

∗∗∗
On considère la fonction f, π-périodique, définie par f(t) = 3t/4 si t∈[0,2π/3] et f(t) = 3(π - t)/2 si t∈]2π/3,π]. Vérifier que f est continue.
Calculer sa valeur moyenne sur [0,π] et donner son développement en série de Fourier. ☼
(Extrait sujet BTS Electronique 1977)

∗∗∗ 
Fonctions ζ de Riemann :  Calcul de ζ(2) , calcul de ζ(4) 

Pour obtenir cette forme, on met la racine carrée de a_n² + b_n² en facteur; notons-là c_n et posons cosΦ_n = a_n/c_n et sinΦ_n = b_n/c_n. On obtient ainsi :

a_ncos nωt + b_nsin nωt = c_n(cos nωt.cosΦ_n + sin nωt.sinΦ_n) = c_n × cos(nωt - Φ_n).

Transformée  de Fourier discrète et théorie du signal :  »      

Dans l'écriture c_n × cos(nωt - Φ_n), le cas n = 1 correspond à l'oscillation fondamentale et au-delà, on parle d'harmoniques de rang n de f, en référence au phénomène sonore des cordes vibrantes et de leur étude par Daniel Bernoulli).

 i  harmonique est dérivé du grec harmonia qui signifiait, en menuiserie et architecture, cheville, assemblage et, par là, ce qui est bien ajusté, c'est à dire harmonieux... La superposition par addition des harmoniques des signaux sonores constituent le timbre caractéristique d'un son. En leur absence (seule présence de l'oscillation fondamentale), on obtiendrait un son plat. Le timbre du piano pour une même note (corde vibrante) est distinct de celui de la clarinette (tuyau sonore). Ce phénomène de timbre fut étudié par Helmholtz et Lissajous.

Notes de musique, gamme, harmoniques :  »

 ➔  Pour chaque harmonique de rang n, de la forme  c_n × sin(ω_nt - Φ_n) :

• le nombre c_n est son amplitude              •  Φ_n est sa phase

• ω_n est sa pulsation (ici nω)                   •  ω_n/2π (= pulsation/2π) est sa fréquence

• ω/2π est la fréquence fondamentale      

• T_n = 2π/ω_n est sa période, inverse de la fréquence. On a en effet : sin[ω_n(t + T_n) - Φ_n] = sin[ω_nt + 2π - f_n] = sin(ω_nt - Φ_n)

∗∗∗
Soit f la fonction impaire 2π-périodique valant 1 sur ]0,π[, nulle en 0 et π.

Montrer que la série de Fourier associée à f est : 4/π × [sin(t) + sin(3t)/3 + sin(5t)/5 + ... + sin(nt)/n + ...]
En faisant abstraction du coefficient multiplicateur 4/π, on a représenté ci-dessous :
sin(t) en noir, sin(t) + sin(3t) en rouge , sin(t) + sin(3t) + sin(5t) en bleu
sin(t) + sin(3t) + sin(5t) + sin(7t) en vert , sin(t) + sin(3t) + sin(5t) + sin(7t) + sin(9t) en magenta

» On constate ci-dessous la superposition par addition des différentes harmoniques.

Zoom de la situation :

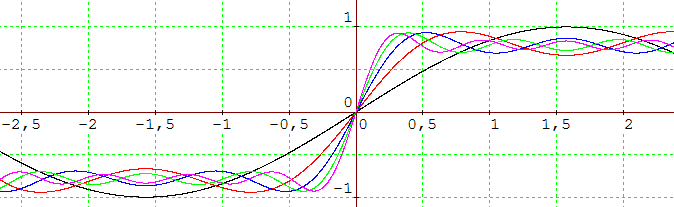
En "poussant" jusqu'à n = 17, on obtient déjà une courbe fort proche de la fonction f donnée. Le passage de -1 à 1 pour les valeurs kπ "se fait de plus en plus" instantanément et la valeur moyenne du signal en ces points tend vers 0.