ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

NASH John Forbes Jr, américain, 1928-2015

Né à Bluefield (Virginie occidentale), fils de John Forbes Nash, électricien texan et de Margaret Virginia Martin, institutrice, John Forbes Nash Jr débute, sans conviction, des études supérieures de chimie au Carnegie Institute of Technology de Pittsburgh (aujourd'hui Carnegie Mellon University). Eu égard à ses aptitudes, ses professeurs lui suggèrent des études de mathématiques.

Nash suit le conseil tout en suivant des cours d'économétrie et s'intéressant aux travaux de John Von Neumann (professeur à Princeton) en théorie des jeux. Suite à un premier article dans la revue économique Econometrica, le brillant étudiant se fait remarquer par Albert W. Tucker qui le fait venir à Princeton où sont en particulier présents, outre von Neumann, le logicien Kurt Gödel et le déjà illustre Albert Einstein, auteur de la théorie de la relativité. Tucker dirigera son doctorat en théorie des jeux (Non-cooperative games, 1950, » réf.12a-12b). On lui doit cette même année, à 22 ans, son célèbre Equilibrium points in n-person games.

»  Berge , Von Neumann , Kakutani

Professeur l'année suivante au Massachusetts Institute of Technology, Nash épouse (1956) Alicia Lardé, physicienne au MIT. De retour à Princeton (1959), il s'adonne aux mathématiques en travaillant sur la très difficile résolution des équations aux dérivées partielles au delà de deux dimensions (plus de 2 variables). On lui doit également des résultats novateurs en géométrie différentielle et algébrique.

Victime d'un accident de la route, John Nash est décédé, ainsi que son épouse Alicia, le 23 mai 2015. Avec Louis Nirenberg, américain d'origine canadienne, professeur à l'université de New-York, il venait de recevoir le prix Abel, considéré comme l'équivalent d'un prix Nobel pour les mathématiques, "pour des contributions frappantes et séminales à la théorie des équations aux dérivées partielles non linéaires et ses applications à l'analyse géométrique".

Plongements de Nash (1954/56) :

En géométrie différentielle, le problème fut de savoir, dans le cas général, si une variété riemannienne (variété différentielle munie d'une métrique intrinsèque) peut être plongée isométriquement (conservation des distances) dans un espace euclidien. Un sujet difficile qui remonte à 1873, étudié par le mathématicien géomètre suisse Ludwig Schläfli (Sur les espaces à courbure constante). Hilbert s'intéressa aussi au problème et, plus récemment, Maurice Janet (1926, » réf.6) et Élie Cartan (1927).

Nash résolut le cas général selon lequel toute variété riemannienne de dimension n sans singularités peut effectivement être plongée dans un espace euclidien à condition que la dimension de ce dernier soit suffisamment grande par rapport à n. Son premier résultat (1954) concerna les variétés de classe C1 (» C1 isometric imbeddings, réf.8a). Le second (1956) s'applique aux variétés de classe Cp (The imbedding problem for Riemannian manifolds, » réf.8b). On pourra consulter la page Wikipedia consacrée au sujet (» réf.7).

 i   Ludwig Schläfli (1814-1885), mathématicien géomètre suisse, élève de Steiner à Berne où il obtient son doctorat en 1860. Son nom est attaché à ses symboles qu'il mit en place pour la nomenclature des polygones et polyèdres réguliers. On pourra consulter la page Wikipedia, bien documentée, consacrée à ces notations (» réf.9).

Polygones réguliers : »            Polyèdres réguliers : »             » Coxeter , Johnson

 i   Maurice Janet (1888-1983), mathématicien français, normalien, agrégé de mathématiques. Après son doctorat, il fut professeur à Nancy et à Caen avant de terminer sa carrière à Paris (Sorbonne) sur une chaire de mécanique céleste (1953-1960). Travaux sur les équations aux dérivées partielles et en géométrie différentielle.

Extrait du mémoire de 1954 :      

(...)

Extrait du mémoire de 1956 :      

Paradoxe de Nash-Kuiper (1954-1955)

 i  Nicolaas Kuiper : mathématicien hollandais (1920-1994), spécialiste en géométrie différentielle. Il étudia à l'université de Leyde où il obtint son doctorat en 1946. Après un séjour aux États-Unis, il obtint (1962) une chaire à l'université d'Amsterdam. Il dirigea l'Institut français des Hautes Études Scientifiques (IHES) de 1971 à 1985.

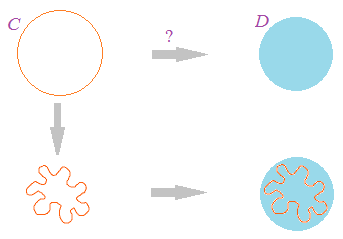
Il s'agit d'un résultat selon lequel une sphère peut être plongée (par difféomorphisme de classe C1 : bijection continûment différentiable ainsi que sa réciproque) dans une boule de rayon inférieur, aussi petit soit-il, sans pour autant contracter les distances. Pour le moins surprenant !

Le résultat étant valide en toute dimension finie, on peut l'illustrer assez simplement en dimension 2 : on considère un élastique de bureau assimilé à un cercle C de rayon 1 (sphère S1, de dimension 1) et un disque D de rayon r < 1 (boule B2 de dimension 2). On peut déformer l'élastique de façon suffisamment lisse (difféomorphisme de classe C1) sans l'étirer ou le contracter afin de pouvoir le placer sur le disque D. Et plus petit sera le rayon du disque, plus "fractale" apparaitra sa "déformation lisse" :

Laissons la parole à Cédric Villani (» réf.11a et 11b) :

 ➔  Pour en savoir plus :

  1. Biographie et travaux de John F. Nash sur le site du prix Nobel

  2. Article du journal Le Monde. fr du 24 mai 2015

  3. The Abel prize 2015 : http://www.abelprize.no/c67203/seksjon/vis.html?tid=67205

  4. Vidéo de la toute dernière conférence de John Nash le 20 mai 2015, trois jours avant son accident mortel au retour d'Oslo, sur site du prix Abel intitulée An interesting equation à l'occasion de l'octroi du prix Abel 2015 avec une intervention préliminaire de Cédric Villani :
    http://www.abelprize.no/artikkel/vis.html?tid=63719.
    » On trouvera sur cette même page l'intervention du colauréat Louis Nirenberg "Some remarks on mathematics"

  5. Les prodigieux théorèmes de Monsieur Nash, conférence de Cédric Villani, une vidéo de l'université de Lorraine :
    http://numerique.univ-lorraine.fr/node/186

  6. Sur la possibilité de plonger un espace riemannien dans un espace euclidien par Maurice Janet (1926), Ann. Soc. polonaise de Mathématique :
    http://rcin.org.pl/Content/15034/WA35_31746_cz159-r1926-T5_Annales-art-4.pdf

  7. Théorème de plongement de Nash sur Wikipedia : https://fr.wikipedia.org/wiki/Théorème_de_plongement_de_Nash

  8. a/ C1 isometric imbeddings sur Jstor (Annals of mathematics, Princeton, 1954) :
    http://www.jstor.org/stable/1969840?seq=1#page_scan_tab_contents (lecture free sur inscription)
    b/ The imbedding problem for Riemannian manifolds sur Jstor (Annals of mathematics, Princeton, 1956) :
    http://www.jstor.org/stable/1969989?seq=1#page_scan_tab_contents (lecture free sur inscription)

  9. Symboles de Schläfli sur Wikipedia : https://fr.wikipedia.org/wiki/Symbole_de_Schläfli

  10. Sur le 17è problème de Hilbert pour les fonctions de Nash :
    http://www.ams.org/proc/1978-071-02/S0002-9939-1978-0486597-2/S0002-9939-1978-0486597-2.pdf

  11. a/ ••• Trois paradoxes relatés par Cédric Villani : (» second paradoxe) : http://histoires-courtes.fr/#page=Villani
    b/ Une page de Cédric Villani où il est question du paradoxe de Nash-Kuiper : http://cedricvillani.org/wp-content/uploads/2012/10/pieuvre.pdf
    c/ Gnash, le tore plat, par Vincent Borelli sur le site Images des mathématiques du CNRS :
        http://images.math.cnrs.fr/Gnash-un-tore-plat.html

  12. Équilibre de Nash :
    a/ Sur le site Le nouvel économiste :
        https://www.lenouveleconomiste.fr/la-theorie-des-jeux-et-lequilibre-de-nash-31766/
    b/ Sur le site du ministère de l'Économie :
        https://www.economie.gouv.fr/facileco/john-nash

Lions Jacques-Louis  Malgrange
© Serge Mehl - www.chronomath.com