Fonction sinus

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Fonctions sinus (d'un angle ou de sa mesure), sinusoïde         ∗∗∗ Exercices
       » Fonctions : cosinus , tangente , cotangente | Arc sinus & arc cosinus , Arc tangente & Arc cotangente
          sinus & cosinus hyperboliques , tangente & cotangente hyperboliques , sécante & cosécante

Nom de la fonction : sinus, abrégé en sin » Girard. C'est une fonction transcendante.
Étymologie : du latin sinus = pli, cavité mais cette racine sémantique est erronée : » Regiomontanus.
Origine : issue des demi-cordes de l'indien Aryabahta.
Ensemble de définition : R.
Périodique : oui, période : 2π » la notion de période

Fonction impaire = sin(-x) = -sin(x).
Fonction dérivée : cos(x), fonction cosinus » calcul de la fonction dérivée
Primitive : - cos(x), opposée de la fonction cosinus » primitive de 1/sin(x)
Nom de la courbe associée : sinusoïde, mot à mot : en forme de sinus (du grec eïdos = forme).

i Étudiée par Leibniz et Newton, la courbe doit sonappellation sinusoïde plus tardivement à Bernard Forest de Belidor (1693-1761), savant français, professeur à l'Ecole d'artillerie de la Fère (Aisne, France), spécialiste en fortifications et en hydraulique, dans son Cours de mathématiques de 1725.

Développement en série : » Leibniz , développements limités usuels

Définitions possibles :

Si l'on considère un angle ^xAy et les perpendiculaires [BC), [B'C'), [B"C"), ... au côté [Ax), la propriété de Thalès permet d'affirmer que les rapports BC/AC, B'C'/AC', B"C"/AC", ... ne dépendent que de l'angle ^xAy. Ces rapports sont le sinus de cet angle.

Le lecteur attentif doit se demander si l'on obtient les mêmes valeurs lorsqu'on préfère tracer des perpendiculaires au côté [Ay) à partir de [Ax)... La question est alors a-t-on BC/AC = DE/AE ?

On se convaincra d'une réponse positive en considérant le triangle où AF = AB et AG = AC, symétriques par rapport à la bissectrice de l'angle ^xAy. On a donc FG/AG = BC/AC = sin^xAy.

En conclusion :

Dans un triangle ABC rectangle en A, le sinus d'un angle aigu (^B ou ^C) est égal au quotient (des mesures) du côté opposé par l'hypoténuse.

Par exemple :

sin^B = AC/BC

Dans un repère orthonormé (O,I,J) orienté par le sens trigonométrique usuel, sin^x = sin^HOM est l'ordonnée OK = HM d'un point M en rotation sur un cercle centré en O, de rayon 1 (cercle trigonométrique), d'où le nom de fonction circulaire, au nombre de trois avec cosinus et tangente (quatre si on admet la cotangente, inverse de la tangente). OH, abscisse de M est le cosinus (cos) de l'angle ^x.

∗∗∗
Montrer géométriquement que sin(90° - x) = cos x en remarquant que si ^HON = 90° - x, alors M et N sont symétriques
par rapport à la bissectrice principale du repère (bissectrice de l'angle ^IJO).

Jean le Rond d'Alembert donnait cette définition (valable si le cercle est de rayon 1...) : ligne droite tirée d'une extrémité d'un arc perpendiculairement sur le rayon qui passe par l'autre extrémité.

Représentation graphique :

La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
OP = arc OM : en déplaçant P, la courbe sinus x → sin(x) apparaît en rouge

Applications :

Elles sont innombrables ! Les fonctions sinus et cosinus sont sans doute les fonctions les plus rencontrées dans les applications scientifiques. En usage dès l'Antiquité en Astronomie, on les rencontre en Électricité (par exemple, le courant EDF est sinusoïdal de fréquence 50Hz, soit de période 1/50), en Mécanique (élasticité, fluidité, marées, ...), en Acoustique (propagation du son), en Électromagnétisme (ondes radios ou hertziennes), en Optique (réfraction), en Topographie (trigonométrie), etc.

» Ptolémée , Aryabhata , Al Battani , Regiomontanus , Roberval

Formules et limites élémentaires, valeurs remarquables : » fonction cosinus

La fonction cosinus (étymologiquement co = associé à) n'est autre que le sinus de l'angle complémentaire;
en mode radians : cos x = sin(π/2 - x), en mode degrés : cos x = sin(90° - x)

Les deux premières formules peuvent être prouvées au moyen du théorème de Ptolémée :

• sin(a + b) = sin a.cos b + sin b.cos a • sin(a - b) = sin a.cos b - sin b.cos a

• sin(a + b + c) = sin a.cos b.cos c + cos a.sin b.cos c + cos a.cos b.sin c - sin a.sin b.sin c

• sin a ± sin b : » formules de transformation de sommes en produits

• sin 2a = 2sin a.cos a | sin²a + cos²a = 1 | sin²a - sin²b = sin(a + b).sin(a - b) | sin²x - cos²x = sin⁴x - cos⁴x

•

• sin(a + b + c) = sin a.cos b.cos c + cos a.sin b.cos c + cos a.cos b.sin c - sin a.sin b.sin c

• sin 3a = 3sin a - 4sin³a | sin 4a = cos a(4sin a - 8sin³a) | sin 5a = 5sin a - 20sin³a + 16sin⁵a

• sin³a = ¼(3sin a - sin 3a) | sin⁴a = (cos 4a - 4cos 2a +3)/8 | sin⁵a = (sin 5a - 5sin 3a + 10sin a)/16

• sin a = sin b ⇔ a = b + 2kπ, k∈Z ou a = π - b + 2kπ, k∈Z

• sin(- a) = - sin a (la fonction sinus est impaire) | sin(π/2 - a) = sin(π/2 + a) = cos a

• sin(π - a) = sin a | sin(π + a) = - sin a | sin(2π ± a) = ± sin a

• sin 0 = 0 | sin(π/6) = sin 30° = 1/2 | sin(π/4) = sin 45° = 1/√2 = √2/2 | sin(π/3) = sin 60°= √3/2

• sin(π/2) = sin 90° = 1 | sin(2π/3) = sin 120° = √3/2 | sin(3π/4) = sin 135° = 1/√2 = √2/2

• » preuve •

➔ Pour d'autres valeurs remarquables, utiliser les propriétés de sinus, par exemple :

• sin(4π/3) = sin(π + π/3) = - sin(π/3) = - √3/2
• sin(7π/4) = sin(2π - π/4) = sin(- π/4) = - sin(π/4) = -1/√2

• Concernant les sinus et cosinus des angles π/5 (36°) , 2π/5, π/10 (18°), 3π/10 : » pentagone et décagone réguliers

• Concernant les sinus, cosinus et tangente de π/12 (15°) et π/8 (22,5°) : » exercice 1 sur la page cosinus

• Formules de transformations de produits en somme ou différence : » Werner Johannes

Conseils aux collégiens :

Apprenez à rédiger sans confondre un angle (ou sa mesure) avec son sinus ou son cosinus... Par exemple :

Dans le triangle ABC ci-dessous, rectangle en A, on suppose AB = 4 cm et BC = 6 cm.

La consigne est Calculer l'angle ^C à 0,1 près. Une rédaction pourra être la suivante :

! La calculatrice affiche 41.8103... : 41,8 est une réponse à 0,1 près par défaut. Il ne faut pas lui fournir à la machine une approximation de la valeur d'un sinus ou d'un cosinus car vous risquez de perdre la (ou les) décimale(s) demandée(s).

Ici, en fournissant 0.66 au lieu de taper la séquence 2 ÷ 3 = sur la calculatrice (pour 2/3), vous trouverez 41.299..., soit 41°, 3 à 0,1 près (par excès) : on est loin de 41,8... Avec 0.666, la 1ère décimale sera juste : 41.759..., soit 41°,8 à 0,1 près (par excès).

Ajoutons que la consigne ne demande pas un arrondi à 0,1 près mais seulement une valeur approchée à 0,1 près qui peut donc être par défaut ou par excès. La réponse ne doit pas excéder 0,1 en plus ou en moins par rapport à la valeur exacte :

On voit sur ce dessin que répondre 41,9 est également une réponse acceptable à 0,1 près mais pas 41,7 ! L'arrondi à 0,1 près est la valeur approchée la plus proche parmi les deux valeurs par défaut et par excès : ici ce sera 41,8.

➔ Si la consigne était à 0,01 près, alors la bonne réponse est 41°,81 (ou 41,82 mais ce ne serait pas très pertinent) et 0.666 comme approximation de 2/3 donnera 41°,76, ce qui serait donc tout à fait faux ! Il faudra fournir 0.6666 pour obtenir 41.805... et le même arrondi 41°,81 (valeur approchée par excès). Enfin, si la consigne était, au degré près, il s'agirait de donner l'entier le plus proche, soit ici : 42°.

Arrondis et troncature : »

Autre cas :

On suppose cette fois AB = 5 cm et ^C = 72°. La consigne est Calculer BC au dixième de millimètre près. Une rédaction pourra être la suivante :

! Mêmes mises en garde que précédemment. L'unité choisie étant le cm, le millimètre correspond au 1/10è de l'unité et le dixième de millimètre correspond au 1/100è de l'unité, d'où le calcul à 0,01 près.

∗∗∗
Exercices niveau collège/lycée

Une courbe sinusoïdale (c'est à dire qui ressemble à une sinusoïde) :

Son équation est y = sin(3x + π/4). Dans la forme y = a.sin(bx + c), a est l'amplitude, b est la pulsation, c est la phase. En sciences physiques (électricité, optique), on écrit traditionnellement ce type d'équation sous la forme y = a.sin(ωt + φ), où t désigne le temps.

Le nombre est alors la fréquence, inverse de la période T = 2π/ω.

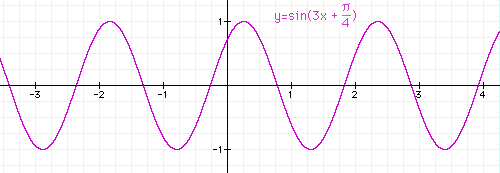
Une courbe plus complexe, superposition de deux signaux sinusoïdaux :

On a choisi ici une équation de la forme y = a.sin(bx) - b.sin(ax) avec b voisin de a. On rencontre ce type de courbe lorsqu'un phénomène oscillant se trouve perturbé par un signal sinusoïdal proche de sa fréquence. Ci-dessous, on a effectué deux "zooms" au voisinage de l'origine :

zoom x 4

zoom x 25

Séries trigonométriques, séries de Fourier : »