ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 CEVA
(Céva) Giovanni,
italien, 1647-1734 |
Né
à Milan, Giovanni Ceva étudia les mathématiques et la physique à Pise, ville de
naissance de Galilée (mort en 1642). Il est le
frère de Tommaso Ceva.
Géomètre et ingénieur accrédité auprès du duc de Mantoue, il enseignera la
géométrie et la mécanique rationnelle en cette ville, prenant plaisir à
apporter, à la manière de Torricelli, des
preuves mécaniques à des sujet a priori purement géométriques.
On lui doit un traité portant sur le concept de centre de gravité d'un système de points (De lineis rectis, 1678), un second (Geometria motus, 1692) étudie les lois régissant le pendule et la composition des mouvements dans le prolongement des travaux de Galilée. Il s'intéressa aussi aux prémisses du calcul différentiel.
Voici un joli théorème de Ceva autrefois étudié dans les classes terminales scientifiques et rencontré aujourd'hui en tant qu'exercice sur les homothéties :
| Théorème de Ceva : |
Trois points P, Q et R étant situés respectivement sur les supports des côtés BC, CA et AB d'un triangle ABC, les droites (AP), (BQ) et (CR) sont concourantes si et seulement si :
» mesures algébriquesOn peut établir ce théorème en tant que théorème dual, au sens projectif, du théorème de Ménélaüs.
Preuve élémentaire :
Selon un résultat relatif au quadrilatère complet, la droite (QR) est la polaire de P par rapport à (QB) et (QC); donc si P' désigne l'intersection de (QR) et (BC), on a :
PB / PC = - P'B / P'C
Or, selon le théorème de Ménélaüs, (QC / QA) × (RA / RB) × (P'B / P'C) = +1 puisque Q, R et P' sont alignés sur les côtés du triangle. On obtient le résultat escompté en remplaçant P'B / P'C par -PB / PC.
Notion de géométrie projective : »
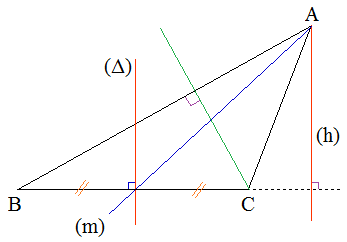
| Cévienne : |
Droite passant par un des sommets d'un triangle et sécante au côté opposé (en tant que segment). Ci-dessous, la hauteur (h) issue de A pour ce triangle ABC n'est pas une cévienne, ni la médiatrice (Δ) de [BC]. Mais la médiane issue de A en est une, ainsi que la hauteur issue de C :
Thomas
Ceva