ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Notion de barycentre (du grec et du latin, mot à mot : centre lourd, pondéré)

Dans son traité « Sur le centre de gravité des surfaces planes », Archimède expose magistralement le concept de centre de gravité, point abstrait où l'on peut considérer que la masse de l'objet s'y concentre et peut être ainsi remplacé, dans les calculs, par ce point pondéré. C'est en quelque sorte le premier traité sur le calcul barycentrique.

Considérons un ensemble fini de points (A_i)_{i = 1,2,...n} du plan ou de l'espace, auxquels on affecte des coefficients (poids) α_i : on parle, historiquement, de système pondéré et on le note souvent : {(A₁,α₁), (A₂,α₂), ... ,(A_n,α_n)}.

♦  Si la somme des α_i est non nulle, alors il existe un unique point G tel que

α₁.GA₁ + α₂GA₂+ ... α_n.GA_n = 0

On dit que G est le barycentre du système pondéré (A_i,α_i).

 ➔  Pour la barre homogène AB ci-dessous, G vérifierait α₁.GA + α₂GB = 0 : les poids seraient α₁ = p et α₂ = p', les vecteurs GA et GB sont de sens contraire. G, centre de gravité de la barre AB, est aussi son point d'équilibre.

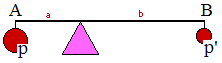
☼ Si A est de poids 2 et B de poids 1, G sera de poids 3 et situé au tiers de [AB] à partir de A car 2GA + GB = 0 signifie que G est entre A et B et GB (longueur) est double de GA. Remarquer que l'on peut utiliser la formule de Chasles pour exprimer : 3GA + AB = 0, soit AG = ¹/₃ AB.

♦  Si O est un point quelconque, la relation barycentrique α₁.GA₁ + α₂GA₂+ ... α_n.GA_n = 0  peut s'écrire, au moyen de la formule de Chasles en décomposant chaque GA_i en OA_i - OG :

On extrait de cette formule les coordonnées de G dans un repère quelconque d'origine O. Notons, pour simplifier m = α₁ + α₂ + ... α_n = Σα_i ("masse" totale du système) on aura :

 Calcul de la position d'une plaque ou d'un volume (centre d'inertie) :  »               »  Leibniz

Si α₁+ α₂+...+ α_k est non nul, alors le barycentre de {(A₁,α₁), (A₂,α₂), ... ,(A_k+1,α_k+1)} est le barycentre de
{(G,α₁+ α₂+...+ α_k),(A_k+1,α_k+1)} où G désigne le barycentre du système {(A₁,α₁), (A₂,α₂), ... ,(A_k,α_k)}.

Le centre de gravité d'un système de points géométriques est le barycentre de ces points tous affectés d'un même poids (coefficient) p non nul. Par définition du barycentre, on peut alors prendre p  = 1. On parle d'isobarycentre (iso = égal).

 !  Le centre de gravité d'un système fini de points matériels peut ne pas être l'isobarycentre si ces points n'ont pas la même masse !

Voici en illustration de cette propriété fondamentale d'associativité deux façons de construire le centre de gravité d'un tétraèdre (les chiffres en rouge sont les poids) :

• Méthode 1 : on construit le barycentre M des 3 sommets de la base; on lui associe le poids 3; G est obtenu en tant que barycentre de {M,3), (S,1)} : G = Bary{(S,1), (A,1), (B,1), (C,1)} = Bary{(M,3),(S,1)}.

• Méthode 2 : on associe deux paires de sommets consécutifs en procédant donc par isobarycentres successifs :
  G = Bary{(S,1), (A,1), (B,1), (C,1)} = Bary{Bary{(A,1),(S,1)}, Bary{(B,1),(C,1)}.

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Pour revenir à la configuration de départ, recharger la page

Étude du centre de gravité du triangle : »              Orthocentre : »             Tétraèdre orthocentrique : »

Lorsqu'une figure n'admet pas de centre de symétrie, la recherche du centre de gravité n'est pas évidente. Voici un résultat du génial Archimède, obtenu aujourd'hui au moyen du calcul intégral : le centre de gravité (centre d'inertie) d'un demi disque homogène est situé en G tel que :

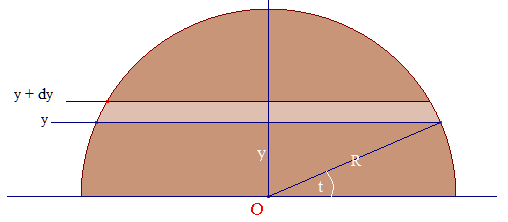
Prouvons ce résultat en remarquant que la plaque admet (quand même...) un axe de symétrie. On choisit comme origine le point O, centre du disque définissant la demi-plaque. La formule précédente pour un nombre fini de points s'écrirait ici :

Dans ce cas continu, découpons la plaque en tranches infinitésimales parallèlement à Ox. à l'ordonnée y, une tranche d'épaisseur dy a une masse dm_y fonction de y et proportionnelle à dy. La somme finie devient une intégrale (principe de l'intégrale de Riemann) :

Notre tranche est assimilable à un rectangle de largeur dy, de longueur L_y vérifiant (théorème de Pythagore) L_y = 2√(R² - y²).

Si ρ est la densité surfacique de la plaque homogène, la masse totale est ρπR². Celle de la demi-plaque est donc m = ½ πR². La masse de la tranche est 2ρ√(R² - y²)dy. Finalement, nous aurons (noter que ρ s'élimine) :

soit :

 ➔  On aurait pu procéder par voie trigonométrique. Avec les notations de la figure, on a y = Rsint, dy = Rcostdt et L_y = 2Rcost. La masse de la tranche est 2ρydy, donc :

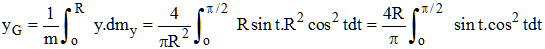
soit :

              C.Q.F.D.

 i  Noter que les théorèmes de Guldin facilitent la recherche d'un centre de gravité tout particulièrement s'il s'agit d'aires ou de volumes de révolution. 

Cas plus général du segment circulaire :     

Un résultat plus général concerne un segment circulaire. On connaît son aire étudiée à cette page, à savoir A  = ½R²(â - sin â), avec ici â = π - 2α. Ce qui fournit La masse totale est alors m = A (par homogénéité, on peut choisir ρ = 1). Exceptée la masse totale m, on a les mêmes formules que précédemment mais ici t varie de α à π/2. On obtient alors :

Si α = 0, on retrouve la formule 4R/3π relative au demi-disque.

 ➔  Lorsqu'il s'agit d'aires ou de volumes de révolution, Les théorèmes de Guldin facilitent la recherche d'un centre de gravité.