ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
» Aire de la surface de révolution engendrée par rotation d'une arche de cycloïde : autour de Ox | autour de Oy |
Le paradoxe des deux roues d'Aristote, étudié tout particulièrement par le philosophe et mathématicien français Blaise Pascal, conduit à l'étude de la cycloïde. Cette appellation est due à Galilée qui connaissait déjà cette courbe. Roberval parla de trochoïde et Pascal de roulette.
Le paradoxe :
Une petite roue (p) de rayon r < R est fixée concentriquement à une grande roue (g) de rayon R. Lorsque la grande roue fait un tour complet, il en est de même de la plus petite. En conséquence, tous les cercles ont même circonférence...

Revenons à notre sujet d'étude :
Considérons un point M d'un cercle (dit cercle directeur) roulant sans glisser sur une droite (d). Imaginez une tête de clou plantée dans le pneu de votre vélo. Lorsque vous roulez sur la route, elle ne tourne pas "en rond"; elle fait des sauts de puce..., plus précisément, elle décrit une cycloïde. Voyons cela :
Pour étudier cette trajectoire, il faut d'abord créer un repère du plan vertical dans lequel se meut le cercle de rayon r (la roue). à un instant to= 0, on repère le point O de (d), la route, en contact avec le cercle et on note M' le point du cercle coïncidant avec O (la tête du clou. On s'intéresse désormais, à chaque instant, au point M diamétralement opposé à M'.
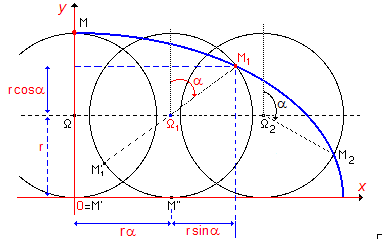
Avec les notations de la figure ci-dessus, lorsque la roue a avancé d'une distance OM", M est en M1 et la distance OM" sur (d) est égale à la longueur de l'arc M'1M". Considérons alors M1(x;y) comme le point générique de la courbe, repéré l'angle α = (Oy,ΩM).
Eu égard à la circonférence du cercle L = 2πr, un arc de cercle correspondant à un angle au centre α exprimé en radians, aura pour longueur L x α/(2π) = αr. Par suite x = αr + r.sinα et y = r + r.cosα.
L'équation paramétrique de la trajectoire du point M est donc fournie par les relations :
x(α) = r(α + sinα) et y(α) = r(1 + cosα)
➔ Dans la littérature mathématique, on trouve souvent l'équation :
x(α) = r(α - sinα) et y(α) = r(1 - cosα)
Cette équation correspond à la "même" cycloïde : Si M(α) désigne le point courant de la 1ère équation, alors celui de la seconde n'est autre que M(α + π).

Tangente et normale :
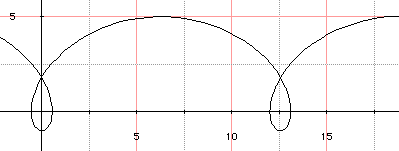
La courbe a l'allure ci-dessous (obtenue par Graphmatica avec r = 1). Le vecteur directeur v de la tangente (t) à la courbe a pour coordonnées (x'(t),y'(t)); on a donc v(r + rcosα , -r.sinα).
A chaque instant, notons maintenant T le point de contact de la cycloïde avec
(d). On a T(rα;0) et TM(r.sinα, r
+ rcosα) : on constate que le produit scalaire v![]() •
•![]() TM
est nul : (TM) est la normale (n) à la courbe au point M :
TM
est nul : (TM) est la normale (n) à la courbe au point M :

|
Génération de la cycloïde : |
La courbe est facilement obtenue grâce à la fonction Report de mesure du logiciel CabriJava pour Internet : si le point de départ est en O, à droite de la figure, le parcours OT de T sur la droite est reporté sur le cercle roulant, ce qui définit un point simulant un roulement sans glissement : longueur arc TM = OT.

Ci-dessous la même figure que ci-dessus générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déplacer T; pour effacer / relancer le
lieu
double-cliquer /
cliquer dans la figure
Wren & rectification de la cycloïde : »
∗∗∗
Aire de la surface de révolution engendrée par rotation d'une arche de
cycloïde :
|
Cycloïde allongée et cycloïde raccourcie : |
Revenons à notre paradoxe. et, pour mieux convaincre, nous supposons que la petite roue (p) roule sur un rail horizontal d : un point m de la circonférence de (p) ne tourne ni, ne roule : il décrit une cycloïde. Quant au point M correspondant de la grande roue (g), il décrit une cycloïde dite allongée.

La trajectoire de M s'obtient facilement à partir de celle de m : avec les notations ci-dessus, on a :
x = r(α + sinα) + (R - r)sinα = rα + Rsinα
y = r(1 + cosα) + (R - r)cosα = r + Rcosα
Dans ce paradoxe, la seule certitude, c'est qu'à l'issue d'une rotation complète de la roue, la distance séparant les positions initiale et finale de m est 2πr : c'est la distance parcourue par le centre des deux roues. Si les roues sont dentées et les axes d et d' remplacés par des crémaillères, le système est -bien entendu- bloqué . Le cas r = R correspondant à la cycloïde (...tout court).
|
Génération des 3 types de cycloïdes : déplacer T; pour effacer/relancer le lieu double-cliquer/cliquer dans la figure |
|
Exemples : |