Développements limités usuels

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quelques séries & développements limités « usuels »

Fonctions algébriques :

     ,    -1 < x < 1
         » ,    -1 < x < 1
     ,    -1 < x < 1

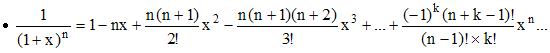| x | ≤ 1
»
| x | ≤ 1

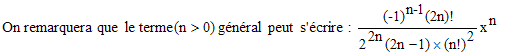
Logarithmes & exponentielles :

ln(1 + x) = x - x²/2 + x³/3 - x⁴/4 + x⁵/5 - ... , (logarithme népérien) , -1 < x ≤ 1
» obtenu par intégration du développement de 1/(1+x). Si x = 1, on obtient ln2
ln(1 - x) = -(x + x²/2 + x³/3 + x⁴/4 + x⁵/5 + ...), -1 ≤ x < 1

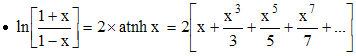, (atnh ou argth = argument tangente hyperbolique) , | x | < 1
» en changeant x en 1/x, on obtiendra le développement de ln[(x+1)/(x-1)] pour | x | > 1

» V. Riccati Fonctions Arg sinus hyperbolique, Arg cosinus hyperbolique, Arg tangente hyperbolique : »

e^x = 1 + x/1! + x²/2! + x³/3! + x⁴/4! + ... + xⁿ/n! , ∀x » Euler
e^-x = 1 - x/1! + x²/2! - x³/3! + x⁴/4! - ... + (-1)ⁿxⁿ/n! , ∀x
e^sinx = 1 + x + x²/2 - x⁴/8 - x⁵/15 - x⁶/240 + x⁷/90... , ∀x
e^{cosx - 1} = 1 - x²/2 + x⁴/6 - 31x⁶/720 - 379x⁸/40320... , ∀x

Trigonométrie :

sin x = x - x³/3! + x⁵/5! - x⁷/7! + ... + (-1)ⁿx²ⁿ⁺¹/(2n+1)! (sinus) , ∀x » Newton
cos x = 1 - x²/2! + x⁴/4! - x⁶/6! + ... + (-1)ⁿx²ⁿ/(2n)! (cosinus) , ∀x
tan x = x + x³/3 + 2x⁵/15 + 17x⁷/315 + ... (tangente) , | x | < π/2
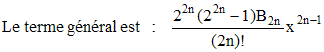» où les B_2n sont les nombres de Bernoulli

On peut obtenir les développements suivants par division suivant les puissances croissantes de x :

cotan x = 1/tan x = 1/x - x/3 - x³/45 - 2x⁵/945 - x⁷/4725 + .. (cotangente) , | x | < π
sec x = 1/cos x = 1 + x²/2 + 5x⁴/24 + 61x⁶/720 + ... (sécante) , | x | < π/2 » Abu al-Wafa
csc x = 1/sin x = 1/x + x/6 + 7x³/360 + 31x⁵/15120 + 127x⁷/604800 + ... (cosécante) , | x | < π

Division de deux polynômes suivantes les puissances croissantes de x : »

(arc sinus) , | x | < 1

(arc cosinus) , | x | < 1

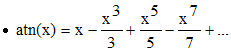(arc tangente) , | x | < 1 » Gregory , Newton , Leibniz

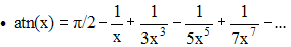(arc cotangente) , x > 1. » si x < -1, ajouter π à ce développement

∗∗∗
1. Montrer que la fonction f(x) = (sin x)⁶ admet x⁶ - x⁸ comme développement limité d'ordre 8 au voisinage de 0 ☼
2. Montrer que la fonction g(x) = ln(cos x) admet -x²/2 - x⁴/12 comme développement limité d'ordre 4 au voisinage de 0 ☼

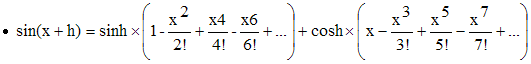
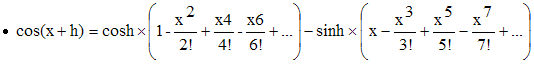
∗∗∗ (polytechnique 1913)
Étude de la fonction θ de la variable x définie par atn(x) = x/(1 + θx²) ☼

Trigonométrie hyperbolique :

sinh x = x + x³/3! + x⁵/5! + x⁷/7! + ... (sinus hyperbolique) , ∀x » Lambert
cosh x = 1 + x²/2! + x⁴/4! + x⁶/6! + ... (cosinus hyperbolique) , ∀x
tanh x = x - x³/3 + 2x⁵/15 -17 x⁷/315 + ... (tangente hyperbolique) , | x | < π/2
où les B_2n sont les nombres de Bernoulli
» Par exemple le coefficient de degré 9 sera (n = 5) : (-1)⁴ x 2¹⁰(2¹⁰ - 1) × 5/66 ÷ 10! = 62/2835
cotanh x = 1/tanh x = 1/x + x/3 -x³/45 + 2x⁵/945 - x⁷/4725 +... (cotangente hyperbolique) , | x | < π
où les B_2n sont les nombres de Bernoulli

Développement des fonctions sécante et cosécante hyperbolique : »

➔ Calculs de développements limités utilisables en ligne :