
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Aires et volumes de révolution | Volume d'une calotte sphérique | volume d'un segment sphérique | Cas paramétrique et polaire Aires et volumes obtenus par intégration (intégrales et triples) |
En première partie, on se propose ici de calculer l'aire (» quadrature) et le volume de la sphère par des considérations géométriques à la manière de Démocrite et d'Archimède.
En seconde partie (clic...), l'usage du calcul intégral que mettront en place Newton et Leibniz, près de 2000 ans plus tard, simplifie grandement la recherche mais n'oublions pas qu'il relève du même principe de découpage en tranches à la manière de Cavalieri !
♦ Étape 1/5 - Aire de la sphère :
On sait ou on admet ici que :
Ces premiers résultats permettent de prouver que :
L'aire latérale engendrée par la révolution d'un segment [AB] (tronc de cône) est 2π × IJ × AB :

Cette aire peut s'écrire 2π × HK × OI en remarquant que IJ × AB = HK
Ce résultat reste valable si A est sur l'axe de révolution ou si AB est parallèle à cet axe.
L'aire latérale d'un contour polygonal s'obtient donc par sommation de chaque aire engendrée (figure ci-dessous à droite).
Dans le cas où le contour polygonal est celui d'un demi polygone régulier de centre O, il apparaît alors que l'aire engendrée est 2π x OI × HK où OI désigne la longueur de l'apothème.
Un cercle étant défini comme la limite d'un polygone régulier dont le nombre de côtés augmente indéfiniment, il suit que l'aire de la sphère de rayon r est 2π × r × 2r car OI tend vers R :
L'aire
d'une sphère de rayon r est 4πr2
»
aire d'un
anneau
sphérique
♦ Étape 2/5 - Volume de la
pyramide :
Le volume d'un prisme est obtenu
en multipliant son aire de base par sa hauteur. Deux prismes ayant même
hauteur et même aire de base sont équivalents (ont
même volume). Deux pyramides ayant même
hauteur et même aire de base sont équivalentes (ont
même volume).
➔
 On considère comme acquis les
résultats suivants :
On considère comme acquis les
résultats suivants :
Considérons alors un prisme ABCA'B'C' triangulaire non nécessairement droit (les faces sont des parallélogrammes). On constate qu'il est composé de trois pyramides triangulaires : CA'B'C', CA'AB et CA'BB'.

CA'B'C'
est équivalente à (a même volume que) A'ABC
qui est égale à CA'AB
: même hauteur (celle du prisme) et bases
équivalentes (même aire).
CA'AB est équivalente à CA'BB' car elles ont même hauteur (distance de C à sa projection sur la face ABB'A' du prisme) et bases équivalentes (A'B partage la face ABB'A' en deux triangles isométriques).
Or, toute pyramide à base polygonale quelconque est décomposable en un nombre fini de pyramides triangulaires de même hauteur. On déduit des considérations précédentes que le volume de la pyramide est :
♦ Étape 3/5 - Volume du cône :
Considérons une pyramide régulière. La base est un polygone régulier de n côtés. Lorsque n devient infini, le contour de base devient un cercle. Un cône peut ainsi être considéré comme une pyramide dont la base polygonale régulière possède un infinité de côtés. On déduit du résultat ci-dessus relatif à la pyramide que le volume du cône de révolution est :
 ♦ Étape 4/5 :
Volume engendré par un contour polygonal :
♦ Étape 4/5 :
Volume engendré par un contour polygonal :
où AH mesure la hauteur du triangle ABC relative à [BC] et SBC l'aire latérale du cône de génératrice BC.
Lorsque le triangle ABC tourne autour d'un axe contenant le seul point A, on obtient par différence un résultat identique.
Par additivité, dans le
cas d'un contour polygonal comme étudié
ci-dessus, en rotation
autour d'un axe, le volume engendré est alors la somme des
volumes engendrés par chaque segment.
Dans le cas d'un demi-polygone régulier de centre O, il apparaît alors que le volume engendré est :
S × OI/3
où S désigne l'aire latérale engendrée par la rotation du contour et OI l'apothème.
Théorèmes de Guldin : »
♦ Dernière étape, Volume de la sphère :
Lorsque le nombre de côtés tend vers l'infini, le contour engendre une sphère d'aire S = 4πR2 (comme précédemment R est la limite de OI, rayon du cercle circonscrit au polygone régulier) et par suite le volume obtenu, volume de la sphère, est 4πR2 × R/3, soit :

Si d = 2R désigne le diamètre de la sphère, on peut aussi retenir :
| Volume d'un solide, volume d'un solide de révolution : |
On suppose connue l'aire A(z) de la surface de cote z du volume étudié (section transversale). Tout comme le calcul d'aire sous une courbe à la manière de Cauchy ou Riemann, un élément différentiel de ce volume assimilé à un cylindre droit est A(z) × dz ("surface de base multiplié par sa hauteur"). Le volume du patatoïde dans un repère cartésien (O,x,y,z) est ainsi donné par la formule :
∗∗∗
camion citerne ,
théorèmes de Guldin
♦ Volume de révolution obtenu par
rotation d'une courbe autour d'un
des axes de coordonnées :
Les
méthodes de calcul, dans le cas de coordonnées cartésiennes y = f(x), d'un
volume de révolution autour d'un des axes de coordonnées, s'appliquent sans
difficultés dans le cas des coordonnées paramétriques ou polaires. La formule ci-dessous,
due à Leibniz dans le cas cartésien, est valable pour
une rotation autour de Ox (axe des abscisses) :
et s'applique
aussi au cas polaire r = φ(t) en posant :
x = r × cost et
y = r × sint
Il s'agira de bien choisir les bornes d'intégration en étudiant
le sens de variation de x en fonction de t.
➔



![]()


♦ Cas de l'ellipsoïde de révolution :
Calculons le volume de l'ellipsoïde de révolution autour de l'axe (Ox) à partir de l'équation paramétrique de l'ellipse x = a.cost, y = b.sint; x devra décrire l'intervalle [-a;+a] :

On intègre pour t variant de π à 2π :
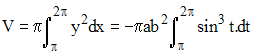
La linéarisation de sin3t = ¼(3sint - sin3t) conduit à :
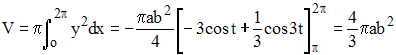
➔ La sphère apparaît comme cas particulier d'ellipsoïde de révolution avec a = b = R, son rayon.
Cas des coordonnées polaires et paramétriques : »
∗∗∗
➔
Dans le cas de la sphère, on
considère le quart de cercle centré en O, de rayon r,
d'équation x2 + y2 = R2 pour
x ≥ 0. Ce qui conduit au volume de la
demi-sphère :

On retrouve ainsi, pour la sphère entière, le volume V = 4πR3/3.
|
Aire de révolution obtenue par rotation d'une courbe autour d'un des axes de coordonnées : |
Un arc de courbe plane rectifiable (Γ) étant définie en coordonnées cartésiennes ou paramétriques par une représentation x = f(t), y = g(t) de classe C
1 au moins, un élément différentiel d'arc de courbe est ds = (dx2 + dy2)1/2. Afin de calculer l'aire engendrée par la rotation d'un arc de courbe autour d'un des axes de coordonnées, par exemple (Ox), on découpe la surface obtenue n en tranches infinitésimales à la manière de l'intégrale de Riemann. Chaque tranche est un tronc de cône d'aire :ΔAi = π × Δsi × [yi + (yi + Δyi)] = 2πyiΔsi + πΔsiΔyi

L'aire est obtenue comme limite pour n infini de la somme des ΔAi sur l'arc de courbe étudié lorsque les Δsi = (Δxi2 + Δyi2)1/2 et, par suite, les Δyi tendent vers 0 :
A = 2π × lim
Δsi→o ΣyiΔsi + π × limΔsi→o ΣΔsiΔyiLa somme ΣΔsiΔyi tend vers 0 par continuité uniforme de g sur l'arc de courbe considéré : en effet, pour n suffisamment grand, il existe h > 0, h tendant vers 0 pour n infini tel que pour tout i : Δyi = |yi+1 - yi| = |g(ti+1) - g(ti)| ≤ h, d'où ΣΔsiΔyi ≤ hΣΔsi. Par suite, si L désigne la longueur de l'arc de courbe considéré : ΣΔsiΔyi ≤ hL → 0. Finalement, et par définition de l'intégrale, les formules suivantes donnent l'aire obtenue par révolution autour de l'axe des abscisses (f3) ou des ordonnées (f4) :
(f3)
A = 2π
∫Γ
y![]() ds
(f4)
A = 2π∫Γ
x
ds
(f4)
A = 2π∫Γ
x![]() ds
ds
Exemple : aire de la surface (paraboloïde) engendrée par l'arc de parabole y = x2/2 par rotation autour de l'axe des ordonnées pour x∈[0,2]. On a ici dy = xdx, donc ds = √(dx2 + dy2) = (1 + x2)dx. A est en u.a. l'intégrale sur [0,2] de x√(1 + x2) qui se ramène à l'intégrale une fonction de la forme u'√u dont une primitive est 2/3 de u3/2. Finalement A = 2π(5√5 - 1)/3.
∗∗∗
Calculer l'aire de la surface engendrée par une arche de
cycloïde tournant
autour de l'axe des abscisses.
Rép. : 64πa2/3.
☼

Un cas plus subtil : l'arche de cycloïde tourne autour d'une tangente de rebroussement
Coordonnées polaires et paramétriques, exemples, exercices : »
| Calcul du volume d'une calotte sphérique au moyen du calcul intégral : |
Lorsqu'un plan "coupe" une sphère, la section obtenue (intersection du plan et de la sphère) est un cercle. Si une boule remplace la sphère, on obtient un disque. Le "morceau" de sphère coloré en bleu est une calotte sphérique.

Cas particuliers :
R désignant le rayon de la sphère, si OH = R, la section se réduit à un point (plan tangent) et si OH = 0, la section est un grand cercle de la sphère : on parlera de cercle équatorial.
∗∗∗
Un plan coupe
une sphère de rayon 7 cm à 4 cm du centre. Quel est le rayon (exact) de la
section ?
Réponse :
√33
cm
Dans le cas général :
Si h = AB est sa "hauteur",
distance entre son sommet A et le plan de section, on obtient le volume en
retirant au volume de la demi-sphère calculé précédemment, à
savoir :

l'intégrale calculée entre 0 et R - h, ce qui revient à calculer l'intégrale entre R - h et R :

fournissant :
Vcal
= πh2(R - h/3) = πh2(3R - h)/3En remarquant le lien entre R, h et le rayon de la section : R
2 = (R - h)2 + r2, soit h2 + r2 = 2hR, on peut obtenir deux autres écritures pour ce volume :V = πh3/6 + ½πhR2 = ½πh(h2/3 + r2)
∗∗∗

| Calcul du volume d'un anneau sphérique : |
On peut s'intéresser
au cas plus général de la portion de sphère obtenue en la coupant par deux
plans parallèles (on parle de segment ou
d'anneau sphérique). En appelant h la distance entre les deux plans, r et r'
(r > r') les rayons des sections,
on obtient facilement par différence des volumes entre les deux calottes de
rayon r et r' :
V
= ½πh(r2
+ r'2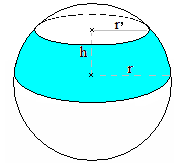
Lorsque r' = 0, on retrouve le volume de la calotte sphérique. L'aire correspondante est A = 2πRh.
| Calcul du volume d'un secteur sphérique : |
Considérons deux points A et B de la sphère situés sur un même méridien (m), grand cercle centré en O et passant par les pôles. Lorsque le méridien (m) tourne autour de l'axe des pôles, le secteur circulaire OAB engendre un secteur sphérique. Comme dans le cas de l'anneau sphérique ci-dessus, appelons h la distance séparant les plans des cercles de section.
∗∗∗ Montrer que le volume engendré est : V = 2πR2h/3 ∗∗∗
