ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Polygones : généralités      » polygones réguliers & constructibilité         i   polygone, du grec poly = plusieurs et gônia = angle.

Un polygone est une ligne brisée fermée (du grec poly = plusieurs et gônia = angle). Voici un polygone ABCDE :

1. Chaque segment de droite qui le constitue, comme [AB] ci-contre, est un côté du polygone. ABCDE possède 5 côtés : c'est un pentagone (du grec penta = cinq et gônia = angle).

2. Les extrémités des côtés sont les sommets du polygone.

3. Tout sommet, comme A ci-dessus, définit ainsi un angle (intérieur) du polygone : dans ce cas de figure, il s'agit de l'angle ^EAB marqué en jaune; on peut aussi le noter tout simplement ^A. Il y a autant d'angles que de côtés.

4. Une diagonale d'un polygone, comme en rose ci-dessus, est un segment joignant deux sommets non consécutifs.

L'appellation des polygones suivant leur nombre de côtés use du grec et du latin :

• n = 3 : triangle : celui qui a trois angles, donc trois côtés; on aurait pu l'appeler trilatère. On distingue quatre cas particuliers, le codage des angles et des côtés indiquent des égalités de mesure :

   triangle quelconque                            triangle isocèle                        triangle équilatéral

               triangle rectangle                           triangle rectangle isocèle

• n = 4 : quadrilatère : celui qui a quatre côtés (du latin quadri = quatre et latus, lateris = côté), donc quatre angles; on pourrait l'appeler un quadrangle... Ci-dessous l'absence de codage signifie aucune particularité :

    quadrilatère quelconque                      trapèze quelconque                             trapèze rectangle              

♦ trapèze tire son nom du grec trapezion = petite table, comptoir, contracté de tetra = quatre et pous = pied. Ce quadrilatère est caractérisé par une paire et une seule de côtés opposés parallèles (» discussion in fine).

    trapèze isocèle                                                  parallélogramme

♦ parallélogramme est issu du grec (puis du latin) parallelus et gramma = tracé, écriture. Ce quadrilatère est caractérisé par deux paires de côtés opposés parallèles.

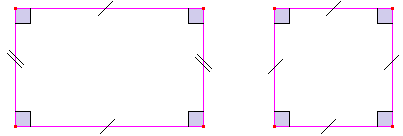
       rectangle                                               carré

♦ rectangle : qui a ses angles droits, du latin directus = direct (» angle droit).
♦ carré : du latin quadrus avec le même sens (quarré en ancien français).

• n = 5 : pentagone : celui qui a 5 angles (du grec penta = cinq et gônia = angle);

• n = 6 : hexagone (du grec hexa = six);

• n = 7 : heptagone (du grec hepta = sept);

  
Ce pylône EDF haute-tension nous montre un exemple d'heptagone         
que l'on pourrait qualifier de "droit et  isocèle" ...

La pulsatille des Alpes (Anemone alpina)
 

• n = 8 : octogone (du latin octo = huit et grec gônia = angle);

• n = 9 : ennéagone (du grec ennêa = neuf);

• n = 10 : décagone (du latin deca = dix);

• n = 11 : hendécagone ou undécagone (du grec  hen = un);

• n = 12 : dodécagone (du latin issu du grec dodeca = douze).
   

• n = 13 : tridécagone;  • n = 14 : tétradécagone;  •  n = 15 : pentadécagone (ou pentédécagone);

• n = 16 : hexadécagone;  •  n = 17 : heptadécagone;  •  n = 18 : octadécagone;

• n = 19 : ennéadécagone;  •  n = 20 : icosagone (du grec icosi = vingt).

Le Pentagon, bâtiment du département de la Défense des États-Unis (Arlington, Virginie)

Polygones réguliers : »

 !  Dès qu'un polygone possède plus de 3 côtés (ou, ce qui revient au même : plus de 3 angles), on doit respecter l'ordre d'écriture des sommets. On obtient le contour (bord extérieur, périmètre) du polygone en suivant la ligne brisée, sans lever le doigt ou le crayon dans l'ordre d'écriture des points : on aborde ainsi le problème des polygones convexes ou croisés décrit ci-après.

• convexe : si, pour toute droite (d) portant un côté, les n - 1 côtés restants sont dans un même demi-plan de bord (d); les exemples bien connus sont le triangle, le trapèze, le parallélogramme, le rectangle, le carré, le losange, ...
  Les angles d'un polygone convexe sont saillants (moindres que l'angle plat, » notion d'angle).

• concave : s'il contient contient au moins un angle rentrant (plus que l'angle plat, » notion d'angle). Cas contraire du précédent.  
• croisé : si au moins deux côtés non consécutifs s'intersectent.
• régulier : lorsque ses côtés et ses angles ont même mesure.

» Les pointillés verts indiquent un exemple de diagonale : elle joint deux sommets non consécutifs.

• étoilé : lorsque ses n sommets sont régulièrement espacés sur un cercle en passant d'un sommet au suivant par rotation d'angle â = 2kπ/n où k est premier avec n (on obtient ses côtés en reliant les sommets de k en k). On peut le qualifier de polygone croisé régulier.

 
pentagone étoilé (k = 2, â = 4π/5, 144°)                  heptagone étoilé (k = 3, â = 6π/7)                        octogone étoilé ( k = 3, â = 3π/4, 135°)          

En savoir plus sur les polygones réguliers convexes, constructibilité : »      Somme des angles : »

» Coxeter et les polygones étoilés

∗∗∗
Nombre de diagonales d'un polygone convexe de n côtés
Au collège, à titre d'exercice de dénombrement, du type problème ouvert, on peut rechercher par essais et conjectures
le nombre de diagonales d'un polygone convexe de n côtés (parfois appelé n-gone).

d = 2 + 3 + ... + (n - 2)

Le résultat peut s'établir directement en classe de 1ère par usage des formules de dénombrement :

C_n²/2 - n = n( n - 1)/2 - n = (n² - 3n)/2

Notion de problème ouvert (en pédagogie) : »

 !  Le carré (rectangle dont la largeur égale la longueur) est un quadrilatère régulier convexe, mais pas le losange (quadrilatère ayant quatre côtés de même mesure) : il est certes convexe mais pas régulier ! à moins qu'il ne soit en fait un carré : losange ayant un 1 droit, et, par suite, 4.

Le terme losange provient de l'arabe  lauza = amande. Dans le sud de la France, certaines tuiles d'ardoise, appelées lauzes évoquent la forme en amande. Depuis Euclide et jusqu'au début du 19è siècle, le losange se disait rhombe (du grec rhombos = toupie, losange). Le parallélogramme (côtés opposés parallèles) s'appelait autrefois rhomboïde (du grec rhombos et de eidos = forme, ressemblance).

 ➔  Au début du 20è siècle, dans un cours de Géométrie (1905), Borel appelait rhomboïde (ci-contre) ou contre-parallélogramme, un quadrilatère dont une diagonale est un axe de symétrie (en forme de cerf-volant).

∗∗∗
Construire à la règle et au compas un hexagone (6 côtés) non régulier dont les côtés ont cependant même mesure
(forme générale de l'enclume du forgeron).

Il est aisé de prouver que la somme des mesures â + ê + ô des angles d'un triangle égale 180° : elle correspondant à un angle plat, soit deux angles droits comme on le comprend ci-dessous. On attribue la preuve de ce résultat aux Pythagoriciens, mais avant eux, Thalès le savait certainement.

De ce résultat, on déduit que la somme s des angles d'un quadrilatère égale 360° (équivalant à celle deux triangles), celle d'un pentagone (cinq côtés) égale 540° (équivalant à celle de 3 triangles) :

D'une façon générale, pour n côtés, on a, en degrés :

car d'un sommet A on peut joindre n - 3 sommets non consécutifs et ainsi former (n - 4) + 2 = n - 2 triangles.

♦ Dans le cas d'un polygone régulier d'angle au centre ^AOB = 360°/n, les angles intérieurs mesurent α = 180 - 360/n, on retrouve  s = n × α = (n - 2) × 180. Les angles extérieurs égalent l'angle au centre.

♦ Dans le cas du triangle, la somme des mesures des angles étant 180°, la mesure d'un angle extérieur, comme ^xBA ci-dessous, est égale à la somme des mesures des deux angles intérieurs non adjacents.

Le statut pédagogique du trapèze n'a jamais été très clair. Dans le bon vieux temps, un trapèze était un quadrilatère convexe
ayant une paire, et une seule, de côtés opposés parallèles.

Cela revenait à dire : quadrilatère convexe ayant deux côtés opposés parallèles et inégaux (qui ne sont pas de même mesure). Les bases étaient, par définition, les côtés parallèles. On note au passage que le parallélogramme, alias rhomboïde, peut se définir par quadrilatère convexe ayant deux côtés opposés parallèles et égaux.

Aujourd'hui, il est de bon aloi d'énoncer :

Un trapèze est un quadrilatère non croisé (convexe) ayant deux côtés opposés parallèles

Et tout cela pour laisser la porte ouverte aux parallélogrammes qui apparaissent alors comme cas particuliers de trapèzes car dire ainsi, tendancieusement, « deux côtés opposés parallèles » n'interdit pas d'en avoir deux autres... : c'est l'idée que deux côtés opposés (au moins) sont parallèles. L'ennui est que l'on complique ainsi des énoncés au détriment de la simplicité du langage. Selon le problème étudié, on devra apporter des précisions comme :

• Considérons un trapèze ABCD  qui ne soit pas un parallélogramme.

• Soit ABCD un trapèze dont les côtés parallèles [AB] et [CD] n'ont pas la même mesure.
• Soit ABCD un trapèze tel que (BC) et (AD) ne soient pas parallèles.
• etc.

→  de gauche à droite un trapèze quelconque, un trapèze rectangle, un trapèze isocèle (tous au au sens strict...)
et le cas particulier du parallélogramme.

» Il est vrai  que pour le parallélogramme et ses complices (rectangle, carré), ou encore les triangles, on apporte parfois des précisions sous la forme : « soit un parallélogramme qui ne soit ni un rectangle ni un carré », « on considère un triangle ABC isocèle (et non équilatéral) ». Mais c'est un tort : voir en conclusion.

 ➔   En ce qui concerne les formules d'aires, la définition new look oblige le professeur, soucieux d'honnêteté intellectuelle, à faire remarquer aux élèves, au risque de les embrouiller alors qu'ils s'y empêtrent déjà, que les formules Bh et (B+b)h/2 coïncident lorsque le trapèze s'avère être un parallélogramme (B = b)...

Professeurs : dites en classe « Tracez un parallélogramme qui ne soit pas un rectangle » en croyant simplifier la consigne avec l'idée très logique qu'un carré est un rectangle et, par là, que les élèves traceront de beaux et "vrais" parallélogrammes. Vous prenez le grand risque de voir se tracer beaucoup des carrés... Dur, dur, la pédagogie. Ce n'est pas gentil de chercher à déstabiliser ses élèves...

Mais qu'est-ce qu'un trapèze isocèle ?  La définition d'antan était claire : on nomme ainsi un trapèze dont les côtés non parallèles ont même mesure. C'est ainsi qu'un trapèze isocèle, comme le triangle isocèle dont il est en quelque sorte un tronc, admet un axe de symétrie. Il nous faut donc exclure le cas du parallélogramme. Par conséquent, on est amené à la définition :

On appelle trapèze isocèle un trapèze qui n'est pas un parallélogramme et dont les côtés
non parallèles ont même mesure.

Viaduc de l'A55 au-dessus du chenal de Caronte à Martigues (bouches-du-Rhône). L = 874 m, h = 50 m.

∗∗∗
Mais qu'est-ce qu'un trapèze rectangle ?  Le lecteur s'évertuera à en donner une définition simple...

En résumé : il faut appeler un chat, un chat et, en l'absence de consigne claire, les cas particuliers devraient être systématiquement prohibés dès le plus jeune âge ! Si, comme à cette page (clic...), on parle de trapèze, il s'agit du trapèze au sens strict : ce n'est pas un parallélogramme, sinon l'énoncé l'aurait dit !

Si un énoncé parle d'un triangle isocèle ABC, il ne s'agit pas d'un triangle équilatéral, etc. Par contre, un prolongement pédagogique intéressant pourra être « que se passerait-il si le trapèze ABCD était remplacé par un parallélogramme... ? ».

En fait, tout cela n'est pas bien grave et quelle que soit la définition que nous donnerons, ringarde ou pas, l'avenir des élèves n'en sera pas changé.
Si polémique il y a, elle se confine à la salle des professeurs à l'heure de la récré.
C'est le serpent de mer à rapprocher de doit-on écrire « le segment AB » ou  « le segment [AB] » ?

Ergotage et sémantique mathématique... : »

∗∗∗
Trapèze isocèle , Trapèze et segment médian , Trapèze et moyenne harmonique