J'apprends à démontrer-6

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

J'apprends à démontrer : caractérisation d'un carré #4 niveau 4ème
» objectif | » #1 , #2 , #3

Rédige le programme de construction de cette figure;
Énonce la question;
Essaie de justifier que IJKL est un ...

Si tu sèches après avoir bien cherché : ››››

Solution :

Énoncé :

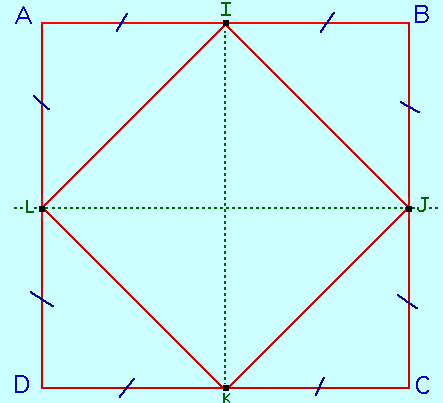
On considère un carré ABCD. On note I, J, K et L les milieux respectifs des côtés [AB], [BC], [CD] et [AD].
Prouver que le quadrilatère IJKL est aussi un carré.

Preuve :

Désignons par m la mesure du côté du carré ABCD : m =AB. Les quatre triangles AIL, IBJ, JCK et KDL sont rectangles isocèles de côté m/2. Ils sont donc isométriques ("égaux" comme on disait dans le bon vieux temps, dans le sens de superposables, donc isométriques... mais ne ressassons pas) et par suite IJKL est un losange.

Mais les angles aigus d'un triangle rectangle isocèle mesurent 45°. Par conséquent :

^JIL = ^AIB - ^AIL - ^BIJ = 180° - 45° - 45° = 90°

Le quadrilatère IJKL est donc un carré en tant que losange ayant un angle droit.

➔ Il existe encore de multiples preuves de ce résultat utilisant symétries, droite des milieux, translations ou rotations. Quelle que soit l'une d'elles, en l'absence de connaissances acquises ou admises comme

les « médianes » d'un carré ont même mesure que son côté et sont perpendiculaires,

elles relèveront du

Mais pourquoi faire simple quand on peut faire compliqué...

Conclusion : En un mot ou presque:

Que revivent les cas d'égalité des triangles !

i On appelle « médiane » d'un quadrilatère, le segment joignant les milieux de côtés opposés