ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
NICOMÈDE, grec, vers -250/-190 (?) |
On ne connaît quasiment rien sur la vie de ce
géomètre grec. Il connut Archimède et vécut sans
doute à Alexandrie.
Nicomède est connu pour sa courbe "trisectrice" qu'il inventa et qu'il construisit mécaniquement, vu l'échec des essais à la règle et au compas, initiés par Hippias d'Elis, pour tenter de construire la trisection de l'angle.
Ce problème célèbre provient
sans doute des essais de construire un polygone régulier de 9
côtés (ennéagone) en essayant, partant du
triangle équilatéral inscrit, de trisecter un arc de 120°,
c'est à dire construire un angle de 40°. On sait, depuis
Gauss
(1801) et Wantzel
(1837) que la trisection de l'angle n'est pas, en
général, résoluble à la règle et
au compas, outils chers à Platon
et Euclide.
La trisectrice de Nicomède est une conchoïde de droite (cliquer sur ce lien pour de plus amples explications).
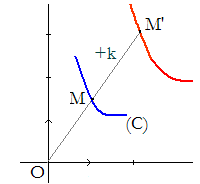
D'une façon générale, une conchoïde d'une courbe (C) relativement à (ou par rapport à) un point O et à un nombre positif k, est obtenue, lorsque M décrit (C), comme le lieu des points M' alignés avec O et M tels que MM' = k.
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ
) :
Pour changer la valeur de k, déplacer le point rouge.
Puis double-cliquez dans le cadre.
Conon de Samos
Dioclès
© Serge Mehl - www.chronomath.com