ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 |
 Le rapporteur :
avantage et piège
de la graduation double à l'intention des jeunes collégiens : 6è-5è |
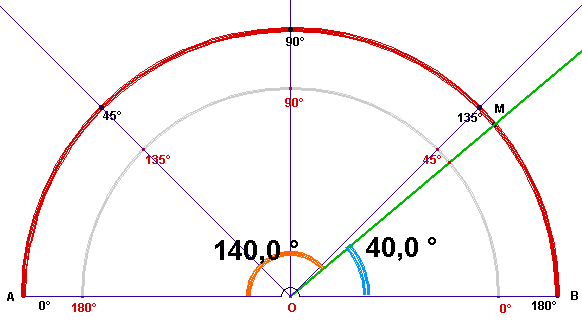
Un rapporteur présentant une unique graduation de 0 à 180° (comme représenté ci-dessus) a l'immense inconvénient de ne pas pouvoir facilement mesurer des angles ouverts à droite car généralement ce type de rapporteur est gradué de 0 à 180° dans le sens des aiguilles d'une montre :
Mesure d'un angle ouvert à droite (angle bleu) :
! avec une
graduation unique, il faut effectuer la soustraction 180 - 140 = 40 !
La quasi totalité des fabricants produisent aujourd'hui des rapporteurs gradués dans les deux sens , et c'est tant mieux.
! Mais il apparaît un piège : la graduation à utiliser pour un angle ouvert à droite (angle bleu ci-dessus) est la graduation intérieure : on doit partir du zéro situé à gauche ! C'est ainsi qu'en classe de 6è, voire 5è, un angle aigu de 40° peut mesurer allègrement 140°.
Tant que l'élève ne maîtrise pas clairement la distinction angle aigu/angle obtus, on ne donne pas encore un sens à la notion de mesure en degrés :
angle aigu ↔ angle inférieur à l'angle droit ↔ mesure inférieure à 90°
angle obtus ↔ angle supérieur à l'angle droit ↔ mesure supérieure à 90°
Cette erreur classique apparaît d'autant plus traîtreusement pour des angles de mesure proche de 90°; par exemple, un angle de 86° dans l'énoncé mesurera 94° (supplément de 86°) sur le dessin de l'élève.
➔ Si votre navigateur accepte les applets Java, la figure animée générée par CabriJava pour Internet illustre cette difficulté :
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ
) :
On peut modifier la mesure de l'angle ^AOM en déplaçant le point M
(le point •, pas
le nom...).
Les angles ^AOM et ^BOM sont
supplémentaires : leur somme mesure 180°.
On peut agrandir/réduire le rapporteur en déplaçant les 0° mais cela sème un
peu la pagaille...
Penser alors à recharger la page.
Voici la même figure en version statique (copie d'écran) :
