ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
Voici une figure de géométrie : les codes te permettent de connaître certaines propriétés de cette figure. Complète le programme de construction afin que quiconque puisse refaire la figure sans ambiguïté.
➔ sans ambiguïté signifie sans erreur possible, conforme à la figure observée
Utilise seulement les mots et lettres indiqués dans le tableau ci-dessous :
| B | O | D | J | K | L | AB |
| BC | (AO) | [AO) | [AC] | coupe | droite | droites |
| angle | passant | intersection | ces | ses | point | Tracer |
| obtus | côté | triangle | bissectrice | hauteur | par | centre |
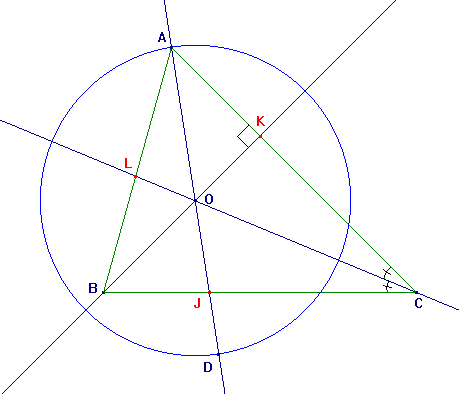
Tracer un ______ ABC (aucun de ____ angles n'étant _____ ). La ______issue de __ coupe le côté ____ en __.
La ______ de l' ____ C ____ le ____ [ __ ] en __.
On note __ le _____ d'__________ de ___ deux ______. La _____ ___ coupe [ __ ] en __;
_____ le cercle de ______ O ______ ___ A; il recoupe ___ en __.
Si tu sèches après avoir bien cherché : ›››› Questions complémentaires (symétrie axiale) : ››››
|
Questions supplémentaires : |
♦ On suppose que la figure est précise et sans erreurs. La demi-droite [OD) est-elle la bissectrice de l’angle ^BOC ? Explique très simplement ta réponse !
♦ En utilisant ton rapporteur, donne, au degré près, la mesure des angles suivants :
^BAC , ^OLA , ^BOC
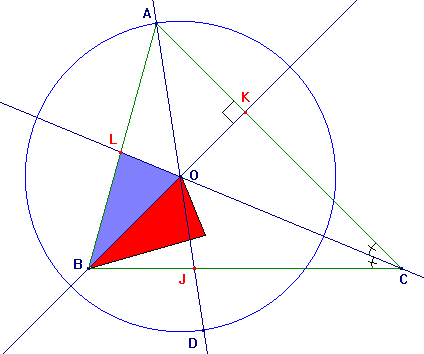
♦ Colorie en bleu le triangle BLO. Tu es bien d’accord que dans la symétrie d’axe (BK), le point J n’est pas le symétrique de L ; explique pourquoi en quelques mots.
♦ Construis maintenant avec soin le symétrique du triangle BLO dans la symétrie
d’axe (BK) et colorie ce symétrique en rouge.
| Réponse : |
Tracer un triangle ABC (aucun de ses angles n'étant obtus);
La hauteur issue de B coupe le côté [AC] en K;
La bissectrice de l'angle C coupe le côté [AB] en L;
On note O le point l'intersection de ces deux droites;
La droite (CO) coupe [AC] en L;
Tracer le cercle de centre O passant par A; il recoupe (AO) en D.

Questions complémentaires (symétrie axiale) : ››››
| Réponse aux questions supplémentaires : |
♦ La demi-droite [OD) n'est pas la bissectrice de l’angle ^BOC car les angles ^BOJ et ^JOC n'ont pas la même mesure : on peut le constater par pliage autour de (AD) ou mesurer les angles : 54° pour ^BOJ et 59° pour ^JOC (au degré près).
♦ En utilisant mon rapporteur, je trouve les mesures suivantes au degré près :
^BAC = 75° , ^OLA = 59° , ^BOC = 113°
♦ Dans la symétrie d’axe (BK), le point J n’est pas le symétrique de L car sinon on devrait avoir BL = BJ et avec mon double-décimètre, je trouve 3,6 cm et 3,2 cm pour ces deux mesures.
♦ Le symétrique du triangle BLO dans la symétrie
d’axe (BK) :