ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Cercles tangents #1       TD niveau 4ème/2nde               » #2 , #3                 
       » tangente à un cercle , angles inscrits & tangente au cercle

1°/  Construire, à la règle et au compas, trois cercles c1, c2 et c3 de rayons distincts donnés et tangents deux à deux extérieurement.


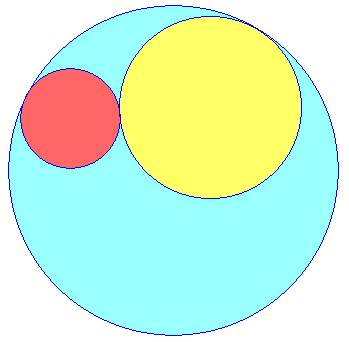
2°/  On donne considère deux cercles c1, c2 de rayons distincts r1 et r2 tangents extérieurement.

a/  Construire un cercle c3 de rayon donné r3 de sorte que  c1 et c2 soient tangents intérieurement à c3. b/  A quelle condition le problème est-il possible ?

Si tu sèches après avoir bien cherché :  ››››
 

© Serge Mehl - www.chronomath.com

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution :

1/° Deux cercles de centres O1 et O2, de rayons respectifs r1 et r2 sont tangents extérieurement si et seulement si O1O2 = r1 + r2.

D'où la construction :

  1. Tracer le cercle (c1) de centre O1, rayon r1.

  2. Tracer un segment O1O2 de longueur r1 + r2 cm.

  3. Tracer le cercle (c2) de centre O2, rayon r2 .
    Les cercles (c1) et (c2) sont tangents extérieurement car O1O2 = r1 + r2.

  4. Les arcs de cercle de centres O1 et O2, de rayons respectifs
    r1 + r3 et r2 + r3 se coupent en O3.
    Le triangle O1O2O3 est constructible car on a bien évidemment (r1 + r3) + (r2 + r3)  >      r1 + r2.

  5. Tracer le cercle de centre O3, de rayon r3.
     (c1) et (c3) d'une part, (c2) et (c3) d'autre part sont tangents extérieurement puisque O1O3 = r1 + r3 et O2O3 = r2 + r3.

2°/  Rappelons que deux cercles de centres O1 et O2, de rayons respectifs r1 et r2 tels que r1 > r2 sont tangents intérieurement si et seulement si O1O2 = r1 - r2.

D'où la construction :

  1. Les arcs de cercle de centres O1 et O2, de rayons respectifs r3 - r1 et r3 - r2 se coupent en O3.

  2. Tracer le cercle de centre O3, de rayon r3.

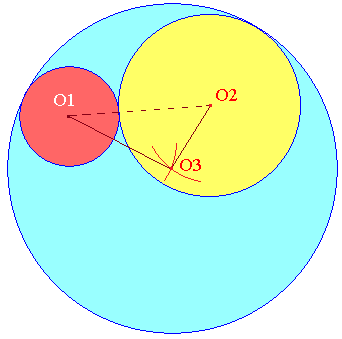
Les cercles (c1) et (c3) d'une part, (c2) et (c3) d'autre part, sont tangents intérieurement puisque O1O3 = r3 - r1 et O2O3 = r3 - r2.

La construction est possible si et seulement si :

r3 > r1 , r3 > r2 et (r3 - r1) + (r3 - r2) > r1 + r2 (inégalité triangulaire), donc si et seulement si :

r3 > r1 + r2

© Serge Mehl - www.chronomath.com